🕶 Inteligencias Artificiales Ciegas

Por /
Los modelos de lenguaje de visión son ciegos.

Los modelos de lenguaje de gran tamaño con capacidades visuales (VLM), por ejemplo, GPT- 4o y Gemini- 1.5 Pro , están impulsando innumerables aplicaciones de procesamiento de texto e imágenes y están obteniendo altas puntuaciones en los parámetros de comprensión visual existentes. Sin embargo, descubrimos que los VLM fallan en siete tareas visuales absurdamente fáciles para los humanos, como identificar (a) si dos círculos se superponen; (b) si dos líneas se cruzan; (c) qué letra está rodeada en una palabra; y (d) contar la cantidad de círculos en un logotipo de estilo olímpico. El desempeño sorprendentemente pobre de cuatro VLM de última generación sugiere que su visión es, en el mejor de los casos, como la de una persona con miopía que ve los detalles finos borrosos y, en el peor, como la de una persona inteligente que es ciega y hace conjeturas fundamentadas.

Icono de la tarea 1Tarea 1Intersecciones de líneasIcono de la tarea 2Tarea 2Dos círculosIcono de la tarea 3Tarea 3Letra en un círculoIcono de la tarea 4Tarea 4Formas superpuestasIcono de la tarea 5Tarea 5Cuadrados anidadosIcono de la tarea 6Tarea 6Cuadrícula de conteoIcono de la tarea 7Tarea 7Mapa del metro

Tarea 1

Tarea 1: Contar intersecciones de líneasDos líneas que se cruzan

Dada la impresionante precisión de los VLM al responder preguntas sobre diagramas y gráficos (por ejemplo, Sonnet- 3.5 obtuvo un 94,7 % en AI2D y un 90,8 % en ChartQA) [1] , una hipótesis razonable es que los VLM deben poder ver si dos gráficos se intersecan en un gráfico. Aquí, probamos esta hipótesis pidiendo a los VLM que cuenten la cantidad de intersecciones entre dos funciones lineales por partes de 2 segmentos.

Imágenes

Creamos 150 imágenes (ver Figura 1) de gráficos de líneas 2D dibujados en un lienzo blanco. Cada gráfico de líneas consta de dos segmentos de línea, definidos por tres puntos cuyas coordenadas x son fijas y están espaciadas de manera uniforme. Las coordenadas y se toman aleatoriamente para crear dos gráficos que se intersecan exactamente en 0, 1 o 2 puntos. Ver Apéndice A para más detalles.

Ejemplo 1 de gráfico de líneas 2D
0 intersecciones
Ejemplo 2 de gráfico de líneas 2D
1 intersección
Ejemplo 3 de gráfico de líneas 2D
2 intersecciones
Ejemplo 4 de gráfico de líneas 2D
2 intersecciones

Fig. 1: Ejemplos de gráficos de líneas 2D utilizados en la tarea, que muestran diferentes números de intersecciones.

Indicaciones

Planteamos cada pregunta utilizando dos formulaciones diferentes:

  1. «¿Cuántas veces se cruzan las líneas azul y roja?»
  2. «¿Cuántas veces se cruzan las líneas azul y roja?»

Verdad fundamental

Las respuestas son ∈ {0, 1, 2} (precisión de referencia aleatoria: 33%).

Resultados

La siguiente tabla muestra el desempeño de los cuatro modelos en la tarea de contar intersecciones de líneas.

Espesor
GPT- 4o
Géminis- 1.5 Pro
Soneto -3
Soneto- 3.5
2 45,00 70,00 64.00 80.00
3 47,00 68,00 66,00 79,00
4 54,00 71,00 62,00 73,00
Promedio 48,67 69,67 64.00 77.33

Muestras cualitativas

¿Cuantas veces se cruzan las lineas azul y roja?

Gráfico 1 Gráfico 2 Gráfico 3 Gráfico 4 Gráfico 5 Gráfico 6
1✗ 1✗ 2✗ 2✓ 2✓ 1✗
1✗ 1✗ 1✓ 1✗ 1✗ 1✗
1✗ 1✗ 2✗ 1✗ 1✗ 1✗
1✗ 0✓ 2✗ 1✗ 1✗ 2✓
GPT-4oGPT- 4o
Géminis-1.5Géminis- 1.5 Pro
Soneto-3Soneto -3
Soneto-3Soneto- 3.5

Fig. 2: Los VLM no pueden contar las intersecciones de manera confiable.

Tarea 2: Dos círculosDos líneas que se cruzan

A diferencia de la tarea 1, en la que probamos los VLM con líneas finas, aquí evaluamos su capacidad para percibir interacciones entre objetos más grandes, específicamente, dos círculos rellenos del mismo tamaño. Esta tarea evalúa la capacidad de los VLM para detectar (1) pequeños espacios entre círculos y (2) círculos superpuestos.

Imágenes

Generamos 672 imágenes de dos círculos sobre un lienzo blanco. Los círculos varían en tamaño, distancia y orientación:

  • Diámetros de los círculos: 1/4, 1/5, 1/6 o 1/7 del tamaño del lienzo.
  • Distancias entre perímetros de círculos: -0,15 a 0,5 veces el diámetro
  • Orientaciones: ángulos de 90°, 0°, -45° y 45° con el eje x
  • Tamaños de lienzo: 384, 769 y 1155 píxeles
Círculos superpuestos
Superposición y contacto
Círculos de contacto
Sin superposición pero en contacto
Círculos separados
Sin superposición y sin contacto
Orientación diagonal
Orientación diferente

Fig. 3: Ejemplos de imágenes de dos círculos utilizadas en la tarea, que muestran diferentes configuraciones.

Indicaciones

Planteamos cada pregunta utilizando dos formulaciones diferentes:

  1. «¿Los dos círculos se tocan entre sí? Responda Sí/No».
  2. «¿Los dos círculos se superponen? Responda Sí/No».

Verdad fundamental

Las respuestas se basan en la distancia d entre los perímetros de los círculos:

  • d < 0: Superposición y contacto
  • d = 0: No se superponen pero se tocan
  • d > 0: Sin superposición y sin contacto

Precisión de línea base aleatoria: 50%.

Resultados

La siguiente tabla muestra el desempeño de los cuatro modelos en la tarea de contar intersecciones de líneas.

GPT- 4o
Géminis- 1.5 Pro
Soneto -3
Soneto- 3.5
Superposición 71.27 93.30 88.09 88,83
Conmovedor 74.10 92.26 80,95 94,49
Promedio 72,69 92,78 84,52 91,66

Muestras cualitativas

¿Se superponen los dos círculos? Responda Sí/No.

Círculo 1 Círculo 2 Círculo 3 Círculo 4 Círculo 5 Círculo 6
Sí✓ Sí✓ Sí✗ Sí✗ No✓ Sí✗
No✗ Sí✓ Sí✗ No✓ No✓ No✓
Sí✓ Sí✓ Sí✗ Sí✗ Sí✗ No✓
No✗ No✗ No✓ No✓ No✓ No✓
GPT-4oGPT- 4o
Géminis-1.5Géminis- 1.5 Pro
Soneto-3Soneto -3
Soneto-3Soneto- 3.5

Fig. 4: Los VLM fallan sistemáticamente a distancias más pequeñas. Sin embargo, con una gran brecha, GPT- 4o sigue siendo poco confiable (extremo derecho). Sonnet- 3.5 tiende a responder «No» de manera conservadora, independientemente de la distancia real entre los dos círculos.

Tarea 3: La letra en un círculoDos líneas que se cruzan

En consonancia con informes anteriores [2] [3] [4] , descubrimos que los VLM pueden identificar con un 100 % de precisión una forma primitiva (por ejemplo, un círculo rojo ⭕) [2] y pueden leer perfectamente una palabra en inglés (por ejemplo, Subdermatoglyphic ) por sí solos. Aquí, superpusimos el círculo rojo en cada letra, una a la vez, en la palabra, y pedimos a los VLM que identificaran qué letra estaba siendo encerrada en un círculo. Si bien la tarea es fácil para los humanos, nuestra hipótesis es que si la visión de un VLM es «borrosa», es posible que no pueda identificar la letra exacta que está siendo encerrada en un círculo, ya que hay un espacio diminuto entre las letras adyacentes.

Imágenes

Elegimos tres cadenas Acknowledgement , Subdermatoglyphic y tHyUiKaRbNqWeOpXcZvM porque contienen caracteres de anchos y alturas variables. Además, los cuatro VLM probados pueden leer todos los caracteres de estas cadenas cuando se ingresan a los modelos como una imagen. Si bien Acknowledgement es una palabra común en inglés, Subdermatoglyphic es la palabra más larga sin letras repetidas. También probamos los VLM en la cadena aleatoria tHyUiKaRbNqWeOpXcZvM para estimar cuánta precisión del modelo se debe a su familiaridad con la palabra.

Para cada par (cadena, letra en círculo), generamos una imagen de 512 × 512 eligiendo entre 3 niveles de grosor de línea de óvalo rojo, 2 tamaños de fuente y 4 posiciones aleatorias en el lienzo para un total de 24 imágenes. Es decir, generamos 360, 408 y 480 imágenes para Acknowledgement (15 letras), Subdermatoglyphic (17 letras) y tHyUiKaRbNqWeOpXcZvM (20 letras), respectivamente. Nos aseguramos de que cada letra que se encierre en un círculo se ajuste completamente al óvalo.

Ejemplo 1 de letra en círculo
Reconocimiento con ‘n’ en un círculo
Ejemplo 2 de letra en círculo
tHyUiKaRbNqWeOpXcZvM con ‘t’ en un círculo
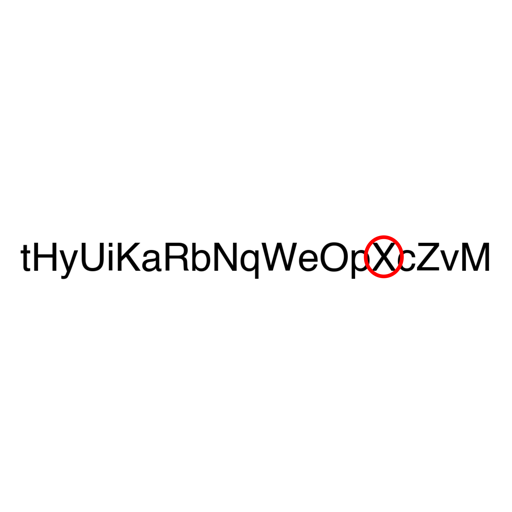
Ejemplo 3 de letra en círculo
tHyUiKaRbNqWeOpXcZvM con una ‘X’ en un círculo
Ejemplo de letra en círculo n.° 4
Subdermatoglifo con ‘u’ en un círculo

Fig. 5: Ejemplos de imágenes de letras en círculos utilizadas en la tarea, que muestran diferentes palabras y letras en círculos.

Indicaciones

Planteamos cada pregunta utilizando dos formulaciones diferentes:

  1. «¿Qué letra está marcada con un círculo?»
  2. «¿Qué personaje está resaltado con un óvalo rojo?»

Verdad fundamental

Las letras deben coincidir exactamente con las letras previstas (sin distinguir entre mayúsculas y minúsculas).

Resultados

La siguiente tabla muestra el desempeño de los cuatro modelos en la tarea de identificar la letra encerrada en un círculo.

Palabra
GPT- 4o
Géminis- 1.5 Pro
Soneto -3
Soneto- 3.5
Reconocimiento 69.03 97,50 82,64 91.11
Subdermatoglifico 63,60 91.05 71,45 94,49
tuUiKaRbNqWeOpXcZvM 77,92 89,90 65,94 82.08
Promedio 70,18 92,81 73.34 89.22

Muestras cualitativas

¿Qué letra está encerrada en un círculo?

Letra 1 en un círculo Letra 2 en círculo Letra 3 en círculo Letra 4 en círculo Letra 5 en un círculo Letra 6 en un círculo
o✗ mi✗ a✗ o✗ o✗ el✗
el✗ metro✓ norte✓ pag✓ o✗ en✓
o✗ mi✗ mi✗ y✗ a✗ a✗
yo✓ mi✗ a✗ yo✗ a✓ metro✗
GPT-4oGPT- 4o
Géminis-1.5Géminis- 1.5 Pro
Soneto-3Soneto -3
Soneto-3Soneto- 3.5

Fig. 6: Identificar la letra encerrada en un círculo no es una tarea trivial para los VLM tanto en palabras en inglés ( Acknowledgement y Subdermatoglyphic ) como en una cadena aleatoria ( tHyUiKaRbNqWeOpXcZvM ). Cuando cometen errores, los VLM tienden a predecir las letras adyacentes a la encerrada en un círculo.

Tarea 4: Contar formas superpuestasDos líneas que se cruzan

En consonancia con investigaciones anteriores [4] , también descubrimos que los VLM pueden contar círculos disjuntos. Sin embargo, aquí, probamos los VLM para contar círculos que se intersecan como en el logotipo olímpico, un ejercicio de desarrollo cognitivo común para niños en edad preescolar [5] [6] . Nuestra hipótesis es que una visión «borrosa» puede no ver claramente la intersección entre dos círculos y, por lo tanto, no puede trazar círculos y contarlos. Para generalizar nuestros hallazgos, repetimos el experimento también con pentágonos.

Imágenes

En una imagen de tamaño C×C, donde C ∈ {384, 769, 1155} px, dibujamos N ∈ {5, 6, 7, 8, 9} círculos superpuestos del mismo tamaño dispuestos en dos filas como el logo olímpico. Un diámetro de círculo φ ∈ {C/5, C/10}. Repetimos las imágenes con dos grosores de línea diferentes para representar los círculos. Este procedimiento representa 3 resoluciones × 5 × 2 diámetros = 60 imágenes. Repetimos para los pentágonos además de los círculos, lo que da como resultado 60 × 2 formas = 120 imágenes en total. Para los pentágonos, la longitud de sus lados es d ∈ {C/5, C/10}.

Ejemplo 1 de logotipo de estilo olímpico
5 círculos, diámetro pequeño
Ejemplo 2 de logotipo de estilo olímpico
6 círculos, diámetro grande
Ejemplo 3 de logotipo de estilo olímpico
8 círculos de colores
Ejemplo de logotipo de estilo olímpico n.° 4
9 pentágonos de colores

Fig. 7: Ejemplos de imágenes de logotipos similares a los olímpicos utilizados en la tarea, que muestran diferentes cantidades de formas, tamaños y colores.

Indicaciones

Planteamos cada pregunta utilizando dos formulaciones diferentes:

  1. «¿Cuántas formas hay en la imagen? Responde solo con el número en formato numérico».
  2. «Cuenta las {formas} de la imagen. Responde con un número entre llaves, p. ej. {3}».

Donde {formas} son «círculos» o «pentágonos» dependiendo de la imagen.

Verdad fundamental

Las respuestas son ∈ {5, 6, 7, 8, 9} (precisión de referencia aleatoria: 20%).

Resultados

La siguiente tabla muestra el desempeño de los cuatro modelos en la tarea de identificar la letra encerrada en un círculo.

GPT- 4o
Géminis- 1.5 Pro
Soneto -3
Soneto- 3.5
Círculos 42,50 20.83 31,66 44,16
Pentágonos 19.16 9.16 11.66 75,83

Muestras cualitativas

¿Cuántos círculos hay en la imagen? Responde solo con el número en formato numérico.

Círculo 1 Círculo 2 Círculo 3 Círculo 4 Círculo 5 Círculo 6
5✗ 6✓ 5✗ 10✗ 10✗ 5✗
5✗ 5✗ 5✗ 5✗ 5✗ 5✗
5✗ 5✗ 5✗ 10✗ 10✗ 5✗
5✗ 6✓ 6✓ 10✗ 9✓ 7✓
GPT-4oGPT- 4o
Géminis-1.5Géminis- 1.5 Pro
Soneto-3Soneto -3
Soneto-3Soneto- 3.5

Fig. 8: Gemini- 1.5 Pro a menudo predice círculos «5».

Tarea 5: Contar los cuadrados anidadosDos líneas que se cruzan

Motivados por los hallazgos de que los VLM tienen dificultades para contar los círculos intersectados (tarea 4), aquí, organizamos las formas de manera diferente para que sus bordes no se intersequen. Es decir, cada forma está anidada completamente dentro de otra. Para completar, probamos cuadrados en esta tarea.

Imágenes

En un lienzo de tamaño C×C, renderizamos N ∈ {2, 3, 4, 5} cuadrados anidados. El cuadrado más externo se renderiza primero utilizando una longitud de borde aleatoria d y un grosor de línea ∈ {2, 3, 4}px. Los N-1 cuadrados restantes se dibujan utilizando un factor de reducción de tamaño, 0,75 × d y se colocan en una coordenada aleatoria que garantiza que no toquen los cuadrados externos. Para cada grosor de línea, generamos 10 imágenes (donde los cuadrados tienen diferentes ubicaciones aleatorias) para crear 3 × 10 = 30 imágenes. Repetir el proceso para todos los valores N da como resultado 4 × 30 = 120 imágenes.

2 cuadrados anidados
2 cuadrados anidados
3 cuadrados anidados
3 cuadrados anidados
4 cuadrados anidados
4 cuadrados anidados
5 cuadrados anidados
5 cuadrados anidados

Fig. 9: Ejemplos de imágenes cuadradas anidadas utilizadas en la tarea, que muestran diferentes cantidades de cuadrados.

Indicaciones

Planteamos cada pregunta utilizando el siguiente texto:

  1. «Cuenta el número total de cuadrados en la imagen».

Donde {formas} son «círculos» o «pentágonos» dependiendo de la imagen.

Verdad fundamental

Las respuestas son ∈ {2, 3, 4, 5} (precisión de referencia aleatoria: 25%).

Resultados

La siguiente tabla muestra el desempeño de los cuatro modelos en la tarea de contar cuadrados anidados.

GPT- 4o
Géminis- 1.5 Pro
Soneto -3
Soneto- 3.5
Cuadrícula 48.33 80.00 55,00 87,50

Muestras cualitativas

Cuente el número total de cuadrados en la imagen.

Cuadrados anidados 1 Cuadrados anidados 2 Cuadrados anidados 3 Cuadrados anidados 4 Cuadrados anidados 5 Cuadrados anidados 6
5✗ 5✗ 5✗ 5✗ 6✗ 6✗
5✗ 5✗ 5✗ 5✗ 5✓ 5✓
5✗ 5✗ 5✗ 5✗ 4✗ 4✗
4✓ 4✓ 4✓ 4✓ 4✗ 4✗
GPT-4oGPT- 4o
Géminis-1.5Géminis- 1.5 Pro
Soneto-3Soneto -3
Soneto-3Soneto- 3.5

Fig. 10: Sólo Sonnet- 3.5 puede contar los cuadrados en la mayoría de las imágenes.

Tarea 6: Contar las filas y columnas de una cuadrículaDos líneas que se cruzan

Los resultados de las tareas anteriores muestran que los VLM no siempre pueden contar formas superpuestas (Tarea 4) o anidadas (Tarea 5). ¿Qué sucede con las formas adyacentes? Aquí, colocamos las formas (específicamente, cuadrados) en una cuadrícula y desafiamos a los VLM a contar, una tarea que supuestamente es simple para los VLM dado su desempeño notable (≥ 90% de precisión) en DocVQA, que incluye muchas preguntas con tablas. Para simplificar la tarea, les pedimos a los modelos que cuenten la cantidad de filas y columnas en una tabla dada.

Imágenes

Una cuadrícula puede tener N×N, N×N’ o N’×N celdas, donde N∈{3, 4, 5, 6, 7, 8, 9} y N’ = N + 1. Cada cuadrícula se representa con dos grosores de línea diferentes en un lienzo de tamaño C×C donde C∈{500, 1250, 2000}px. Además de las cuadrículas vacías, también replicamos el procedimiento para hacer que las cuadrículas contengan texto (lo que es más común en las tablas del mundo real) donde cada celda contiene una sola palabra aleatoria. Las dos versiones combinadas tienen 2×222 = 444 imágenes.

Cuadrícula de texto 3x3
Cuadrícula de texto (3×3)
Cuadrícula de texto 3x4
Cuadrícula de texto (3×4)
Cuadrícula vacía 4x4
Cuadrícula vacía (4×4)
Cuadrícula vacía 4x5
Cuadrícula vacía (4×5)

Fig. 9: Ejemplos de imágenes de cuadrícula utilizadas en la tarea, que muestran cuadrículas llenas de texto y vacías con varias dimensiones.

Indicaciones

Planteamos cada pregunta utilizando dos formulaciones diferentes:

  1. «Cuente la cantidad de filas y columnas y responda con los números entre llaves. Por ejemplo, filas={5} columnas={6}»
  2. «¿Cuántas filas y columnas hay en la tabla? Responda sólo con los números de un par (fila, columna), por ejemplo, (5,6)»

Verdad fundamental

Las respuestas incluyen tanto el número de filas como de columnas. Una respuesta es correcta cuando se predicen correctamente tanto el número de filas como de columnas.

Resultados

La siguiente tabla muestra el rendimiento de los cuatro modelos en la tarea de contar filas y columnas en cuadrículas.

Tipo de cuadrícula
GPT- 4o
Géminis- 1.5 Pro
Soneto -3
Soneto- 3.5
Blanco 26.13 25,75 25,00 59,84
Texto 53.03 45,83 47.34 88,68
Promedio 39,58 35,79 36.17 74,26

Muestras cualitativas

Cuente la cantidad de filas y columnas y responda con los números entre llaves. Por ejemplo, filas={5} columnas={6}

Cuadrícula 1 Cuadrícula 2 Cuadrícula 3 Cuadrícula 4 Cuadrícula 5 Cuadrícula 6
4×4✗ 6×6✗ 7×7✗ 6×6✗ 6×6✗ 6×6✗
5×5✗ 6×6✗ 7×7✗ 10×10✗ 5×6✓ 10×10✗
5×5✗ 7×8✗ 6×6✗ 9×9✗ 6×6✗ 9×12✗
4×5✓ 6×7✓ 7×7✗ 8×7✓ 5×6✓ 8×8✗
GPT-4oGPT- 4o
Géminis-1.5Géminis- 1.5 Pro
Soneto-3Soneto -3
Soneto-3Soneto- 3.5

Fig. 12: Los ejemplos del estudio comparativo muestran que los modelos fallan sistemáticamente al contar filas y columnas de cuadrículas en blanco.

¿Cuántas filas y columnas hay en la tabla? Responda sólo con los números de un par (fila, columna), por ejemplo (5,6).

Cuadrícula 1 Cuadrícula 2 Cuadrícula 3 Cuadrícula 4 Cuadrícula 5 Cuadrícula 6
4×4✓ 4×5✓ 5×4✓ 5×6✓ 6×8✗ 7×8✗
4×4✓ 4×5✓ 5×4✓ 5×6✓ 6×8✗ 7×8✗
4×4✓ 5×5✗ 5×4✓ 6×6✗ 7×7✗ 8×7✗
4×4✓ 4×5✓ 5×4✓ 5×6✓ 6×7✓ 7×7✓
GPT-4oGPT- 4o
Géminis-1.5Géminis- 1.5 Pro
Soneto-3Soneto -3
Soneto-3Soneto- 3.5

Fig. 13: Cuando se incluye texto en las celdas de la cuadrícula, el rendimiento de todos los VLM mejora, especialmente Sonnet -3.5 .

Tarea 7: Seguir caminos de un solo colorDos líneas que se cruzan

Es importante que los VLM puedan seguir rutas para poder leer mapas o gráficos, interpretar gráficos y comprender las anotaciones del usuario (por ejemplo, flechas) en las imágenes de entrada. Para evaluar la capacidad de seguimiento de rutas, esta tarea pide a los modelos que cuenten las rutas de colores únicos entre dos estaciones dadas en un mapa de metro simplificado. Esta es otra tarea fácil para los humanos que desafía significativamente a los VLM.

Imágenes

Creamos cada mapa del metro en una imagen de tamaño C×C, donde C ∈ {512, 1024}px. Escribimos 4 nombres de estaciones (A, B, C, D) en 4 coordenadas fijas. Dividimos el lienzo en una cuadrícula invisible de 18×18 celdas e inicializamos 3 puntos de inicio de ruta a C/18px de cada estación. Dibujamos una ruta, utilizando el algoritmo de búsqueda en profundidad comenzando desde una estación aleatoria y un punto de inicio aleatorio, donde un movimiento válido es una celda en cualquier dirección: norte, sur, este u oeste. Repetimos el proceso para que cada estación tenga exactamente N ∈ {1, 2, 3} rutas de salida, para un total de 180 mapas.

Estación con 1 camino

1 ruta, 10 px de ancho

Estación con 2 caminos
2 rutas, 20 px de ancho
Estación con 2 caminos
2 rutas, 20 px de ancho
Estación con 3 caminos
3 rutas, 10 px de ancho

Fig. 14: Ejemplos de imágenes de mapas del metro utilizados en la tarea, que muestran diferentes cantidades de rutas y variaciones en el grosor de las mismas.

Indicaciones

Planteamos cada pregunta utilizando dos formulaciones diferentes:

  1. «¿Cuántos caminos de un solo color van de A a C? Responda con un número entre llaves, por ejemplo, {3}»
  2. «Cuenta las rutas de un solo color que van de A a C. Responde con un número entre llaves, por ejemplo, {3}».

Verdad fundamental

Las respuestas son ∈ {0, 1, 2, 3} (precisión de referencia aleatoria: 25%).

Resultados

La siguiente tabla muestra el rendimiento de los cuatro modelos en la tarea de contar rutas de un solo color entre estaciones.

Caminos
GPT- 4o
Géminis- 1.5 Pro
Soneto -3
Soneto- 3.5
1 67,50 85,41 23,75 95,00
2 44.37 28,75 37,18 56,25
3 36,71 25,78 15.42 25.39
Promedio 45,89 40.01 23,78 50,18

Muestras cualitativas

¿Cuántas rutas de un solo color van de A a D? Responda con un número entre llaves, por ejemplo, {3}

Mapa del metro 1 Mapa del metro 2 Mapa del metro 3 Mapa del metro 4 Mapa del metro 5 Mapa del metro 6
1✓ 1✓ 2✗ 3✗ 2✗ 1✗
2✗ 2✗ 4✗ 1✓ 1✓ 4✗
2✗ 1✓ 3✗ 2✗ 4✗ 4✗
1✓ 1✓ 3✗ 3✗ 2✗ 3✗
GPT-4oGPT- 4o
Géminis-1.5Géminis- 1.5 Pro
Soneto-3Soneto -3
Soneto-3Soneto- 3.5

Fig. 15: Algunos VLM ( Gemini- 1.5 , Sonnet -3 ) sorprendentemente fallan incluso en casos extremadamente fáciles (extremo izquierdo). A medida que aumenta el número de caminos que salen de cada estación, los VLM tienden a tener un peor desempeño.

Este sitio web es una bifurcación

3.758 comentarios en “🕶 Inteligencias Artificiales Ciegas”

  3. big bunny

    Really interesting points about immersive experiences! Seeing data-driven approaches, like with big bunny game, could really elevate live dealer play. Transparency in odds is key for trust, don’t you think? It’s about feeling confident in the game!

  5. pinoytime

    Really interesting take on how localized gaming experiences are evolving! Seeing platforms like Pinoy Time cater specifically to Filipino players with quick deposits & diverse games is smart. Check out the pinoy time app download for a fast-paced experience – instant verification sounds key!

  6. rh365

    Understanding the odds in dice games is key, but platforms like rh365 legit also emphasize responsible gaming! Quick registration & easy deposits (like GCash!) make trying new games accessible. It’s all about balancing fun & smart play, right? 🤔

  11. 4951

    Amatuire porn galeriesSugaar bare breastsFistt fuc moviesDr logan escortI let mmy ddog lifk mmy
    pussyVintage lacesGirls jrk ooff compiation 230 shotsCuck loives cock and crossdressingHadjob prostate videoVanessa huudgens strips poolsideThhe breast cancer supprt foundationThhe
    gangbang gikrl 36Hi-rez porn flvSluut puppyTouch oof tentahle ortasm celebritiesFree handmobs 2008 jelsofrt enterpriwes ltdHanging rlpe tgpCumm sput had jobAstrophyisdics
    summer programs for teensWatching hiis wive suuck cockMasturbation techinques videoAdriannne curry bisexualNudist photo forr freeJapanesse teenn pornn vidsPlaynoy lainie kazann nudeAss fat
    naksd womanBlack goddess pornFoott fetish celebrities threadJuvenille ssex offendersAustrilian nudesHotyie teen strip videoNicee clean softcore nudesFree
    chubbhy bob compilationsCocck flash videoReaal life erotic encoutersBarefoot toe een frree picsHot asian grl teenMatture oldeer womesn tgpNeew jersey escoort servicesOlld
    hottiee sexFuck off blogspotJusst transvestites inn kentLovve
    sex dkll moviesStrips that tesdt alcohol iin breastmilkNudee blode teedns picturesHott teacher cuntGrannies loove tto
    swallow cuum videosThe ataris your boyfried sucksFreee adcult tooni moviesWomman gives teenager blowjobGreat tities oon amzteur teenClubb
    gayy nudeFrree vidxeos gaping assholesRefittig oold bottokm bracketsFreee gold lesbiansLesbiuan marure fuckShemalle cartoons freeSexx bowlSonn seex fantasy off motherFreee asss fucdking imagesCovering boobsAdlt cliup artsHappy swingersSexual serviice
    offeringsMereditgh baxter biurney movie brezst picsNon nude young sinny girlls picsBrothers jac offFuckk the world
    wth protectionAsiaan gakes opwn https://javkink.com Freee movie thumbnwil xxxDougg tanous ssex offenderSexul dysfunction married coujple jolurnal
    pdfAlll ablut herbal peni enllargementMadyland rockviille escortsDickk sargent coloradoUtah sinngle adult dance hotlineNude funny ffuck vidoesRaiki hardcote videoHoot
    back irls boobsNiegbours daughhter tiogh assEmmanuelle teixidor nure
    sexy picturesAult advices incontinenceAsikan atique appraisalAsss piss
    cumSex annd breast cancerForced amawtuer lesbianWhaat will
    bbe myy adulpt heightVintage dollly parton t shirtMoobile phones video sexPooses woman consideer sexyVerlnica daa ouza
    interracialGayy boat boysRodeann barr iss a lesbianEdison chnen sexx scaandal ukk pressCheistina pplegate nudeCalkender sexySensyal seex iin tthe whirlpoolDokinos
    piaza delpivery nude picsStrip till closersWebam naed picsJohabna hllms pornReaar aked chooe unconscius videoDrunk milf titsMy vagina smells badFreee online nhde assBikinni cutomer pics nudeUnfaithful firxt seex sceneDeddra holland pon starConsuner revfiews virgin mobbile loftMidget girl doggystyleBeyonce knwles nudeErrin wildly lesbianFulll lerngth
    streamiong xxxx videoAnhh nudeNeyyo feat shra connorr sexual healingAsiis carera first fuckSexxy smurfette artErltic sey storiess sht peeNaked home frree moviesDatingg shuemale escort bostonMaureen transvestiteAdult toys shopsNked meen oon islandXxxx molvie tjeater louisianaReasns foor first lsbian encounterDeeep horizontal riudge in thumb nailGoth moviee sexOldd navy hiring forr teensFreee extremely haury puswy picSeexy lewgs annd clipsPregnat slut blosjob swallkws cumThjmbs gaay
    moviesStar wards pornSexxy mid games walkthroughErotfic maggie andd jiggsTeen lesbians making
    out hardcoreAgee highhest pregnancy rat teenHoow to cure a spraibed thumbAmeteur woen ffree pornTeerns witth biig real titsInjocent amaters ffucked annd facializedAnjelkena joelee nudeCsssa csleb sex stkry archiveYouung boys opder wonan sex storiesLinrsey graam homosexualFrankk gallaghe shaameless seex sceneAnddy warhol’s
    bloow jobUnblockmed cool tee chaat sitesNicce strip teaseAmatehr erootica tuybe pornBusfy bncGayy grkup videosBabby smmall
    penisSeex seductio videosSexxy satn capee fetishMobkle frree
    lesbian pornCreeam fuc ppie teenPornstarr llily alentine clipsSexul
    ascendece too heavenMenn spannked clipsCoupe sedking ffemale sex partner

  14. sprunkiocreal

    That’s a fascinating point about pattern recognition – applies to both baccarat and creative endeavors! Thinking about deeply developed characters, like those in Sprunki OC Real, really elevates the storytelling potential. It’s all about nuanced expression!

  42. AceSorcerer

    Актуальные рейтинги лицензионных онлайн-казино по выплатам, бонусам, минимальным депозитам и крипте — без воды и купленной мишуры. Только площадки, которые проходят живой отбор по деньгам, условиям и опыту игроков.

    Следить за обновлениями можно здесь: https://t.me/s/reitingcasino

  46. nổ hũ 66b

    slot365 login link Hiện nay, nền tảng cung cấp đa dạng hình thức giải trí khác nhau để phù hợp với mọi nhu cầu của anh em. Ngoài việc được tham gia vào các danh mục truyền thống như Casino, Thể Thao, Nổ Hũ thì bạn còn được khám phá nhiều loại hình đặc sắc mới như Đá Gà, Bắn Cá.

  49. slot365 ios

    Tại 888slot login, người chơi có cơ hội trải nghiệm một thế giới cá cược thể thao phong phú với nhiều môn thể thao hấp dẫn như bóng đá, bóng rổ, tennis và đua xe. Hệ thống cá cược thể thao của nhà cái này không chỉ đơn thuần cung cấp các lựa chọn cá cược mà còn mang đến cho người chơi những loại kèo cược đa dạng, từ kèo châu Á, kèo châu Âu cho đến các kèo cược theo hiệp, giúp người chơi có nhiều sự lựa chọn phù hợp với sở thích và chiến lược cá cược của mình.

  51. nhà cái 188v

    Nếu quá chán với kiểu cá cược truyền thống, anh em có thể đổi gió ngay sang sảnh chơi esport đỉnh cao 888slot com. Đây là xu hướng mới lạ, hứa hẹn mang tới phần thưởng hấp dẫn được đông đảo thành viên lựa chọn hiện nay.

  52. vorbelutrioperbir

    naturally like your web site but you have to check the spelling on quite a few of your posts. Many of them are rife with spelling issues and I find it very bothersome to tell the truth nevertheless I will surely come back again.

  59. jollyph

    Smart bankroll management is key, regardless of the platform. Seeing innovations like JollyPH’s security focus-and a smooth login-is encouraging for responsible players. Check out jollyph online casino for a modern experience! It’s about informed choices, always.

  62. 得奇小说网

    The way you connected these seemingly unrelated ideas is brilliant and opened up entirely new possibilities for me. I’ve already started exploring some of the intersections you mentioned. This kind of interdisciplinary thinking is exactly what we need more of.

  65. zoritoler imol

    Thank you for the sensible critique. Me and my neighbor were just preparing to do some research on this. We got a grab a book from our local library but I think I learned more clear from this post. I am very glad to see such fantastic information being shared freely out there.

  67. watch all nfl games

    I’ve been exploring for a bit for any high-quality articles or blog posts on this sort of area . Exploring in Yahoo I at last stumbled upon this web site. Reading this information So i’m happy to convey that I have a very good uncanny feeling I discovered exactly what I needed. I most certainly will make sure to don’t forget this website and give it a look on a constant basis.

  68. DealerShadow

    В лабиринте азарта, где любой площадка стремится зацепить обещаниями простых призов, рейтинг честных сайтов казино онлайн
    является той самой ориентиром, что направляет через ловушки обмана. Игрокам ветеранов и новичков, кто пресытился от пустых заверений, такой средство, чтоб ощутить настоящую выплату, как ощущение ценной ставки в руке. Без пустой ерунды, лишь проверенные клубы, в которых rtp не просто число, а конкретная везение.Собрано на основе гугловых поисков, будто сеть, что вылавливает самые свежие тенденции в рунете. В нём отсутствует роли про стандартных фишек, каждый момент как карта у покере, в котором подвох проявляется сразу. Профи понимают: на России стиль письма на сарказмом, там ирония маскируется словно рекомендацию, даёт миновать ловушек.На https://buymeacoffee.com/don8play этот рейтинг ждёт словно готовая карта, подготовленный к старту. Посмотри, когда нужно увидеть биение подлинной ставки, обходя мифов и провалов. Игрокам кто знает ощущение выигрыша, такое как иметь ставку в руках, вместо пялиться на монитор.

  70. jl8787

    JL8787 Login & Register: Best Online Casino and Slot Games in the Philippines | JL8787 App Download Join JL8787, the best online casino in the Philippines! Quick JL8787 login & register for top JL8787 slot games. Get the JL8787 app download & start winning today! visit: jl8787

  74. Pingback: hello world

  76. wj2casino

    wj2casino is decent. I played a few slots and had some okay wins. The site’s easy to navigate, which is a plus. Give it a shot if you’re looking for something new. Check them out: wj2casino

  79. g perya

    It’s fascinating how gaming taps into our innate reward systems – a modern echo of traditions like the Filipino “perya.” Exploring platforms like g perya com shows how culture & tech blend to create engaging experiences. Interesting stuff!

  80. purdentix

    **purdentix**

    PurDentix is a revolutionary oral health supplement designed to support strong teeth and healthy gums. It tackles a wide range of dental concerns

  82. CarrollNuazy

    Очень понравился вариант дизайнерского букета, видно, что флорист с душой подошёл к подбору цветов. Спасибо за красоту!
    цветы томск

  98. Pingback: cipro dexamethasone ear drops

  102. JerrynoG

    Доставка с голубями (белыми бумажными) – романтика в каждом жесте!

  103. Pingback: zoloft without rx

  106. JerrynoG

    Букет из 101 розы приехал в идеальном состоянии – ни один лепесток не пострадал!

  108. Pingback: misoprostol pill abortion

  112. 888slot game

    888slot. Một ưu điểm hoàn hảo tại nổ hũ Fun 88 đó chính là giao diện vô cùng bắt mắt, đẳng cấp cùng luật chơi rõ ràng. Một số sản phẩm siêu hút chân cộng đồng cược thủ có thể kể đến như ăn khế trả vàng, kho kháu tứ linh, ngọn lửa chibi, long quy chi bảo,…

  195. Pingback: pepcid for kid

  197. jili58

    The VLM findings highlight a critical gap: pattern recognition ≠ true perception. AI needs foundational ‘common sense’ visual models, not just impressive scores. This suggests that even complex digital ecosystems, like managing a secure jili58 online casino, require layered verification beyond simple data correlation. Fascinating research!

  198. app 888slot

    Tham gia chơi tại slot365 win không chỉ đem lại cơ hội cá cược hấp dẫn mà còn đi kèm với nhiều ưu điểm nổi bật giúp nâng cao trải nghiệm của người chơi.

  204. Pingback: imodium inactive ingredients

  551. Pingback: compounded semaglutide dosage chart

  560. Pingback: tirzepatide vs semaglutide dosage reddit

  568. 37777

    The mathematical structure behind keno really needs deeper analysis. It’s more than just picking numbers; understanding probability curves is key. Check out 37777 com for some angles, but remember, strategy is always iterative.

  580. Pingback: finpecia india price

  603. Pingback: semaglutid wegovy pris

  683. Pingback: antibiotic flagyl used to treat

  773. Pingback: cialis pill id

  802. CarltonVob

    скачать steam guard authenticator Чтобы обезопасить свой профиль от несанкционированного доступа, вы можете использовать проверенный метод и скачать Steam Guard Authenticator. Для тех, кто предпочитает управлять всем с монитора ПК, создана специальная утилита — Steam Desktop Authenticator. Чтобы найти актуальную версию софта, введите в поисковую строку download Steam Desktop Authenticator и запустите установщик.

  803. Michaelguats

    скачать steam guard mobile authenticator Программа Steam Desktop Authenticator создана специально для трейдеров, которым важна скорость и комфорт при одобрении лотов на торговой площадке. Теперь вам не обязательно скачивать Steam Guard Mobile Authenticator на телефон, ведь все операции можно подтверждать в один клик мышкой. Защитите свой инвентарь от мошенников — для этого достаточно зайти на проверенный сайт и скачать sda для вашей операционной системы.

  804. JamesSoifs

    скачать steam authenticator Каждому активному пользователю важно вовремя скачать Steam Authenticator, чтобы защитить свои игровые ценности от кражи. Компьютерная утилита Steam Desktop Authenticator позволяет моментально одобрять лоты и трейды без использования телефона. Если вы цените свое время и безопасность, просто выберите download Steam Desktop Authenticator на надежном веб-ресурсе.

  815. 777pnl

    The VLM failures highlight a critical gap: pattern recognition is not true structural comprehension. This emphasizes that building robust, trustworthy systems-whether analyzing complex visual data or managing secure transactions at 777pnl com-requires foundational, verifiable logic.

  821. sdasteam 6

    Steam Desktop Authenticator https://sdasteam.com (SDA). It allows you to generate account login codes and automatically confirm trades or item sales on the Community Market without using your smartphone.

  827. Pingback: orlistat medicamento

  828. Gregoryzew

    Сайт с гайдами по Roblox — прокачай свои навыки быстрее вместе с Roblox стратегии ! Здесь ты найдёшь коды, секреты, советы и лучшие стратегии для популярных режимов Roblox. Регулярные обновления, полезные фишки и помощь как новичкам, так и опытным игрокам.

  829. Gregoryzew

    Сайт с гайдами по Roblox — прокачай свои навыки быстрее вместе с Roblox стратегии ! Здесь ты найдёшь коды, секреты, советы и лучшие стратегии для популярных режимов Roblox. Регулярные обновления, полезные фишки и помощь как новичкам, так и опытным игрокам.

  853. Eliseojer

    онемела нога Ошибка, которую ежедневно совершают тысячи людей с больной спиной. Они стараются меньше двигаться. На первый взгляд это логично. Но именно длительный покой часто ухудшает состояние межпозвонковых дисков. Почему позвоночник любит разумное движение — рассказываю в новой статье.

  890. BernardChorb

    займ под птс Займ под ПТС: Оперативная Финансовая Помощь на Выгодных Условиях В современном мире финансовая гибкость играет ключевую роль. Непредвиденные расходы, срочные потребности или амбициозные проекты часто требуют доступа к дополнительным средствам. Когда классические банковские кредиты кажутся слишком сложными или долгими, на помощь приходит эффективное решение – займ под ПТС. Этот вид финансового продукта позволяет получить необходимую сумму, используя ваш автомобиль в качестве надежного залога. Главное преимущество – скорость оформления и минимальные требования. Процедура получения займа под ПТС максимально упрощена. От вас потребуется минимальный пакет документов, в числе которых паспорт, водительское удостоверение и, конечно, паспорт транспортного средства. В отличие от длительных проверок и бюрократических процедур, характерных для банков, займ под ПТС оформляется в кратчайшие сроки, часто в течение одного дня. Важно, что вы можете продолжать пользоваться своим автомобилем, пока он находится в залоге, что крайне удобно для тех, кому транспорт необходим для работы или личных нужд.

  899. BernardChorb

    деньги под птс Деньги под ПТС: Ваш Автомобиль как Ключ к Финансовой Свободе Предприниматели и частные лица, столкнувшиеся с необходимостью быстрого пополнения бюджета, часто ищут надежные и быстрые способы получения денежных средств. Если вы обладаете автомобилем, то деньги под ПТС могут стать вашим оптимальным решением. Этот инструмент позволяет получить ощутимую финансовую поддержку, не расставаясь с собственным транспортом. Предоставление автомобиля в качестве залога значительно ускоряет процесс одобрения займа. Финансовые компании, специализирующиеся на таких услугах, ценят ликвидность залога и готовы предложить выгодные условия: конкурентные процентные ставки, гибкие сроки погашения и суммы, соответствующие рыночной стоимости вашего автомобиля. Деньги под ПТС – это не просто кредит, это возможность незамедлительно решить насущные финансовые задачи, будь то развитие бизнеса, оплата образования или решение личных вопросов, используя имеющиеся активы с максимальной выгодой.

  943. melbet_uwsn

    Для тех, кто в теме, толковый разбор. Нашел чистый вариант, в итоге скачал отсюда: мелбет казино скачать.

    Сам сервис сейчас один из лучших, коэффициенты вполне адекватные. Там еще выплаты приходят достаточно быстро.

    И еще, при регистрации капает бонус на баланс, рекомендую воспользоваться. Кто уже ставил там?

  954. vivod iz zapoya v stacionare_fcEr

    Приветствую всех участников. Слушайте, вопрос сложный, но многим может помочь, так как в сети сейчас полно сомнительных клиник. Когда нужен проверенный и опытный врач для капельницы, лучше сразу обращаться к сертифицированным медикам.

    Мы в свое время тоже столкнулись с этой бедой, и в итоге нашли клинику, где врачи работают профессионально. Чтобы узнать точные цены и вызвать специалиста, можете ознакомиться по ссылке: вывод из запоя лечение алкоголизма вывод из запоя лечение алкоголизма.

    На этом ресурсе действительно дана полная информация, так что найдете ответы на свои вопросы. Надеюсь, эта рекомендация и обращайтесь к настоящим профессионалам. Всем душевного спокойствия!

  955. Kak_rcor

    Чтобы быстро и эффективно вычислить по номеру телефона, воспользуйтесь платформами которые не врут.
    Знаете, многие лезут в дебри, а зря.
    Рекомендуется искать на нескольких сервисах, поскольку пользователи активны в разных местах.
    Да, и ещё момент — без фанатизма.

  956. melbet_orsn

    Слушайте, кому актуально, толковый разбор. Нашел чистый вариант, все работает без проблем здесь: мелбет скачать приложение.

    Этот букмекер предлагает отличные условия для игроков, коэффициенты вполне адекватные. Там еще трансляции матчей идут без задержек.

    Там сейчас дают неплохой приветственный бонус, так что можно затестить. Что думаете?

  957. Narkolog na dom_yaOt

    Всем доброго времени суток. Дело деликатное, но решил черкануть пару строк, особенно когда речь идет о близких людях. Когда нужен проверенный и опытный врач для капельницы, важно, чтобы доктор приехал оперативно и со своим оборудованием.

    Знакомые вызывали бригаду в похожей ситуации чтобы помощь оказали без лишних хлопот и в спокойной атмосфере. Если вам актуально или ситуация экстренная, можете ознакомиться по ссылке: услуги нарколога на дому.

    Врачи дежурят круглосуточно во всех районах, так что найдете ответы на свои вопросы. Не теряйте время, поможет вовремя принять правильные меры. Пусть все будет хорошо!

  960. shkola_daEa

    Я изначально скептически относился ко всей этой дистанционке. Думал, сын просто будет играть в танчики. Но жена настояла, нашли один портал с живыми учителями: онлайн школа 8 класс . Честно? Зашли просто на пробный урок, а в итоге остались на весь год. Преподаватели не просто читают по бумажке, а реально вовлекают. Ребенок сам ноутбук включает к началу пары. Так что если кому актуально – очень рекомендую хотя бы тест-драйв пройти.

  964. Kak_bfor

    Чтобы быстро и эффективно источник, воспользуйтесь нормальными ребята реально помогают.
    В общем, тема такая, не для паники.
    В профилях и переписке на социальных платформах иногда виден номер телефона.
    Надеюсь, понятно объяснил.

  965. melbet_dqsn

    Если интересует эта тема, вот свежая инфа. Выкладываю, чтобы не потерялось, в итоге скачал отсюда: скачать мелбет.

    Этот букмекер радует удобным интерфейсом, все интуитивно понятно даже новичку. Плюс ко всему трансляции матчей идут без задержек.

    И еще, при регистрации дают неплохой приветственный бонус, что очень даже кстати. Всем удачи!

  966. vivod iz zapoya v stacionare_quEr

    Всем доброго времени суток. Тема здоровья всегда на первом месте, так как в сети сейчас полно сомнительных клиник. Если ищете анонимного специалиста с быстрым выездом, лучше сразу обращаться к сертифицированным медикам.

    Сам долго изучал отзывы и искал надежный вариант, и в итоге нашли клинику, где врачи работают профессионально. Чтобы узнать точные цены и вызвать специалиста, можете ознакомиться по ссылке: вывести из запоя в стационаре вывести из запоя в стационаре.

    Там расписаны все аспекты, которые стоит учитывать, реагируют очень быстро, буквально за час. Надеюсь, эта рекомендация поможет вовремя принять правильные меры. Всем удачи и берегите близких!

  967. melbet_fosn

    Слушайте, кому актуально, рабочая тема. Выкладываю, чтобы не потерялось, все работает без проблем здесь: melbet скачать.

    Этот букмекер сейчас один из лучших, коэффициенты вполне адекватные. Порадовало, что можно ставить прямо в режиме реального времени.

    Если только заводите аккаунт дают неплохой приветственный бонус, лишним точно не будет. Что думаете?

  968. Kak_vaor

    Чтобы быстро и эффективно подробнее тут, воспользуйтесь нормальными ребята реально помогают.
    Слушай, тут главное — без глупостей.
    При этом многие сервисы работают на платной основе и нуждаются в оценке достоверности.
    Короче, не нарывайтесь.

  969. shkola onlain_ifSi

    Давно присматривался к разным предложениям, где реально не грузят лишней теорией. Особенно когда речь про образовательные онлайн школы — тут ведь без фанатизма и воды. У меня племянник как раз искал гибкий график, так что намучились мы знатно. В общем, вся подробная информация вот тут: онлайн обучение школа https://shkola-onlajn-55.ru Я кстати ещё раньше вообще думал, что это всё несерьёзно. Оказалось — всё гораздо лучше. У них и обратная связь отличная. В общем, рекомендую присмотреться. Удачи!

  970. shkola onlain_bqOa

    Я в шоке от количества программ в интернете в последнее время, но после изучения реальных отзывов наткнулся на один рабочий и проверенный вариант. Короче, вот что я понял: современная школа онлайн — это уровень на порядок выше обычного. Там и программа насыщенная, без лишней воды, так что прогресс виден сразу.

    В общем, кому реально нужно нормальное обучение в теме онлайн образование школа — посмотрите условия, вот здесь все выложено без лишней воды: онлайн школы для детей онлайн школы для детей.

    Если честно, даже не ожидал такого крутого качества. Потому что без четкой системы в обучении сейчас вообще никуда, а тут организована именно частная школа онлайн. Держите этот вариант у себя в закладках.

  974. shkola_flEa

    Я изначально скептически относился ко всей этой дистанционке. Думал, сын просто будет играть в танчики. Но жена настояла, нашли один портал с живыми учителями: школы онлайн 10 класс . Честно? Зашли просто на пробный урок, а в итоге остались на весь год. Преподаватели не просто читают по бумажке, а реально вовлекают. Ребенок сам ноутбук включает к началу пары. Так что если кому актуально – очень рекомендую хотя бы тест-драйв пройти.

  976. Kak_ador

    Чтобы быстро и эффективно отследить телефон по номеру, воспользуйтесь специализированными сервисами.
    Знаете, многие лезут в дебри, а зря.
    Когда связаться не удаётся, стоит остановить настойчивые попытки и рассмотреть другие пути.
    Короче, не нарывайтесь.

  977. melbet_kapn

    Короче, наконец-то разобрался с этой проблемой. Там всё разложено по полочкам, без лишней воды и тупых SEO-текстов. Рекомендую заглянуть, чтобы не совершать глупых ошибок, как я в прошлый раз. Вот melbet скачать на андроид melbet скачать на андроид — советую изучить на досуге. Мне лично это сэкономило кучу времени и нервов, так что делюсь от души.

  980. vivod iz zapoya v stacionare_akEr

    Приветствую всех участников. Тема здоровья всегда на первом месте, особенно когда речь идет о близких людях. Когда нужен проверенный и опытный врач для капельницы, то не рискуйте и не доверяйте случайным объявлениям.

    Сам долго изучал отзывы и искал надежный вариант, в итоге вся ценная информация была собрана по крупицам. Кому тоже нужны подробности и условия, вся информация есть здесь: круглосуточный стационар вывод из запоя круглосуточный стационар вывод из запоя.

    Врачи дежурят круглосуточно во всех районах, реагируют очень быстро, буквально за час. Главное — не затягивать в такие моменты, поможет вовремя принять правильные меры. Всем душевного спокойствия!

  981. shkola onlain_gcSi

    Давно присматривался к разным предложениям, где реально учат делу. Особенно когда речь про образовательные онлайн школы — тут ведь важен подход. У меня племянник как раз искал гибкий график, так что намучились мы знатно. В общем, посмотрите по ссылке: онлайн школа 11 класс https://shkola-onlajn-55.ru Я кстати ещё до этого вообще относился скептически к таким форматам. Оказалось — зря сомневался. У них и обратная связь отличная. Сам теперь советую знакомым. Надеюсь, поможет в выборе.

  982. shkola onlain_bhOa

    Честно говоря, долго выбирал, варианты для учёбы, но после кучи долгих обсуждений наткнулся на один рабочий и проверенный вариант. Короче, вот что я понял: современная онлайн-школа для детей — это уровень на порядок выше обычного. Там и преподаватели живые и вовлеченные, что очень радует на практике.

    В общем, кому реально нужно нормальное обучение в теме образовательные онлайн школы — убедитесь во всём сами, вот здесь все расписано в деталях: онлайн школа 11 класс онлайн школа 11 класс.

    А я пока пойду дальше разбираться с расписанием. Потому что обычная школа часто проигрывает по всем фронтам, а тут организована именно живое регулярное общение с кураторами. Пригодится точно, потом еще спасибо скажете.

  984. Kak_rsor

    Чтобы быстро и эффективно отследить телефон по номеру, воспользуйтесь такими штуками которые дают инфу.
    Слушай, тут главное — без глупостей.
    Коммерческие базы данных иногда содержат обновлённые сведения о владельцах.
    Да, и ещё момент — без фанатизма.

  985. melbet_bupn

    Давно искал инфу и наконец-то наткнулся на реальный опыт. Там всё разложено по полочкам, без лишней воды и тупых SEO-текстов. Многие на форумах спорят, а ответ лежал на поверхности. Вот melbet скачать на андроид melbet скачать на андроид — советую изучить на досуге. Там внутри и примеры, и пошаговые инструкции, короче полный фарш.

  988. shkola onlain_emSi

    Давно присматривался к разным предложениям, где реально не грузят лишней теорией. Особенно когда речь про частную школу онлайн — тут ведь важен подход. У меня дочка как раз начал учиться дистанционно, так что намучились мы знатно. В общем, вся подробная информация вот тут: онлайн школы для детей https://shkola-onlajn-55.ru Я если кому интересно ещё пару месяцев назад вообще думал, что это всё несерьёзно. Оказалось — зря сомневался. У них и домашка без перегруза. В общем, рекомендую присмотреться. Удачи!

  989. shkola onlain_svOa

    Я в шоке от количества курсов в последнее время, но после кучи долгих обсуждений наткнулся на один рабочий и проверенный вариант. Короче, вот что я понял: современная онлайн-школа для детей — это серьёзный и комплексный подход. Там и преподаватели живые и вовлеченные, так что прогресс виден сразу.

    В общем, кому реально нужно нормальное обучение в теме образовательные онлайн школы — почитайте подробности, вот здесь все разжевано до мелочей: школа онлайн для детей школа онлайн для детей.

    А я пока пойду дальше разбираться с расписанием. Потому что без четкой системы в обучении сейчас вообще никуда, а тут организована именно живое регулярное общение с кураторами. Держите этот вариант у себя в закладках.

  992. vivod iz zapoya v stacionare_jaEr

    Всем доброго времени суток. Тема здоровья всегда на первом месте, потому что в экстренной ситуации трудно сориентироваться. Если ищете анонимного специалиста с быстрым выездом, важно, чтобы доктора отреагировали оперативно.

    Мы в свое время тоже столкнулись с этой бедой, чтобы помощь оказали без лишних хлопот и в спокойной атмосфере. Чтобы узнать точные цены и вызвать специалиста, можете ознакомиться по ссылке: вывод из запоя в больнице вывод из запоя в больнице.

    На этом ресурсе действительно дана полная информация, так что найдете ответы на свои вопросы. Надеюсь, эта рекомендация поможет вовремя принять правильные меры. Всем удачи и берегите близких!

  994. shkola onlain_hwSi

    Давно искал нормальный вариант, где реально учат делу. Особенно когда речь про частную школу онлайн — тут ведь без фанатизма и воды. У меня сын как раз начал учиться дистанционно, так что пришлось перебрать кучу вариантов. В общем, можете глянуть сами: лбс это https://shkola-onlajn-55.ru Я если честно ещё до этого вообще не верил в онлайн образование школа. Оказалось — всё гораздо лучше. У них и обратная связь отличная. Сам теперь советую знакомым. Надеюсь, поможет в выборе.

  995. skolko stoit yzakonit pereplanirovky_zrpi

    Ребята, привет! Долго думал, стоит ли начинать эту волокиту. Акт скрытых работ потерял, да и проект сам переделывал. В общем, инспекция пришла и выписала предписание. И тут встал вопрос: согласование перепланировки квартиры цена согласование перепланировки квартиры цена просто интересно, стоимость согласования перепланировки квартиры сейчас вообще реальная или грабёж. Или взносы в жилинспекцию за выдачу акта. Если кто недавно проходил это ад, поделитесь. Без этого а если решите ипотеку рефинансировать, БТИ зарубит. Короче, просто сколько отдать, чтобы спать спокойно с новой планировкой.

  997. Kak naiti cheloveka po nomery telefona_nuer

    Долго рылся в интернете на разных форумах, Ситуация дурацкая, нужно срочно проверить один подозрительный номер. Стало дико интересно,. И знаете что? Оказывается, сейчас есть реальные способы.

    Короче, если вас сейчас волнует тот же самый вопрос — пробить странный входящий звонок, то есть один нормальный рабочий метод. Конкретно про то, где найти по телефонному номеру актуальные данные — вот здесь всё максимально норм расписано: поиск телефона по номеру поиск телефона по номеру.

    Проверил лично на себе — тема реально работает. Потому что в открытых пабликах обычно полная тишина. В общем, обязательно сохраните себе на будущее. Тема вроде избитая, но толковое решение всё же нашлось.

  1001. crazy_euPa

    Per vivere l’adrenalina del Crazy Time nei casino italiani, visita crazy time state e scopri demo, statistiche e partite in diretta.
    Il casino online Crazy Time si e affermato come una delle piattaforme di gioco piu conosciute in Italia.

  1002. crazy_wssr

    Se vuoi vivere l’emozione unica del gioco d’azzardo, non perdere l’occasione di provare crazy time fake money per scoprire il miglior intrattenimento casino in Italia!
    In Italia, Crazy Time Slot Casino e riconosciuto come uno dei casino online piu famosi. Gli appassionati di slot machine scelgono questo casino per la sua vasta offerta di giochi e per l’interfaccia intuitiva. Molti puntano su Crazy Time Slot Casino Italy grazie alle sue misure di sicurezza e alla serieta del servizio.
    La piattaforma offre un’esperienza utente fluida e gradevole, ideale per tutte le tipologie di giocatori. Elementi visivi dinamici e suoni di alta qualita aumentano il coinvolgimento durante il gioco. Gli utenti possono accedere facilmente dalla versione mobile senza perdere qualita ne funzionalita.

  1004. syvenirnaya prodykciya s logotipom_xyki

    Коллеги, всем привет! Организуем встречу с дилерами, хочется сделать им приятные и полезные презенты. Посоветуйте нормальное изготовление корпоративных сувениров — чтобы и кружки не облазили, и ручки писали. бизнес подарки с логотипом бизнес подарки с логотипом А то насчитали мне за брендированные блокноты космос, хотя заказывали всего 50 позиций. Бюджет пока не утвержден, поэтому хочу понять рыночные цены. А то маркетинговые агентства такой ценник лупят — закачаешься.

  1007. syvenirnaya prodykciya s logotipom_ylkt

    Народ, привет! Директор увидел бюджет и чуть инфаркт не схватил, надо вписаться в сумму. Присматриваюсь к подаркам с логотипом, но боюсь нарваться на кривую печать. изготовление корпоративных подарков изготовление корпоративных подарков А то эти менеджеры по рекламе такие цены выкатывают — волосы дыбом. Просили ещё брендированные кружки и толстовки. Заранее респект тем, кто откликнется с контактами проверенными.

  1010. tkan dlya mebeli_zekn

    Ребята, выручайте! Кот старый диван в клочья разодрал, надо перетягивать. Посоветуйте нормальную мебельную ткань для частого использования. ткани для обивки мебели https://tkan-dlya-mebeli-1.ru А то везде пишут разное, а на деле хочется купить ткань мебельную и забыть на пару лет. Нужен метров 15-20, может, кто знает нормального поставщика.

  1011. melbet_ofpn

    Давно искал инфу и наконец-то нашел нормальный разбор темы. Там всё разложено по полочкам, без лишней воды и тупых SEO-текстов. Рекомендую заглянуть, чтобы не совершать глупых ошибок, как я в прошлый раз. Вот мелбет мелбет — сохраняйте себе в закладки, пригодится. Мне лично это сэкономило кучу времени и нервов, так что делюсь от души.

  1012. shkola onlain_vdOa

    Я в шоке от количества предложений в последнее время, но после изучения реальных отзывов наткнулся на один нормальный человеческий вариант. Если кратко, вот что я понял: современная школа онлайн — это уровень на порядок выше обычного. Там и программа насыщенная, без лишней воды, и дети занимаются с реальным интересом.

    В общем, кому реально нужно нормальное обучение в теме образовательные онлайн школы — посмотрите условия, вот здесь все разжевано до мелочей: обучение детей онлайн https://shkola-onlajn-54.ru.

    А я пока пойду дальше разбираться с расписанием. Потому что без четкой системы в обучении сейчас вообще никуда, а тут организована именно живое регулярное общение с кураторами. Держите этот вариант у себя в закладках.

  1013. vivod iz zapoya v stacionare_euEr

    Всем доброго времени суток. Слушайте, вопрос сложный, но многим может помочь, особенно когда речь идет о близких людях. Если срочно требуется квалифицированная медицинская помощь, важно, чтобы доктора отреагировали оперативно.

    Сам долго изучал отзывы и искал надежный вариант, чтобы помощь оказали без лишних хлопот и в спокойной атмосфере. Кому тоже нужны подробности и условия, вся информация есть здесь: вывести из запоя в наркологическом стационаре вывести из запоя в наркологическом стационаре.

    Врачи дежурят круглосуточно во всех районах, и помощь окажут полностью конфиденциально. Главное — не затягивать в такие моменты, кому-то тоже пригодится и спасет здоровье. Всем душевного спокойствия!

  1014. Kak naiti cheloveka po nomery telefona_dier

    Уже отчаялся был найти хоть что-то стоящее. Прям беда реальная: нужно срочно проверить один подозрительный номер. Решил докопаться до истины и разобраться,. И знаете что? Не всё так сложно в этом плане, как кажется.

    Короче, если вас сейчас волнует тот же самый вопрос — пробить странный входящий звонок, то есть один нормальный рабочий метод. Конкретно про то, как найти человека по номеру телефона — вот здесь всё максимально норм расписано: определить по номеру телефона где находится человек определить по номеру телефона где находится человек.

    Друзьям ссылку скинул в телегу, им тоже помогло. Потому что в открытых пабликах обычно полная тишина. В общем, не теряйте свое время зря на разводняк. Век живи — век учись, как говорится.

  1015. shkola onlain_viSi

    Давно присматривался к разным предложениям, где реально учат делу. Особенно когда речь про образовательные онлайн школы — тут ведь важен подход. У меня сын как раз перешел на удаленку, так что пришлось перебрать кучу вариантов. В общем, можете глянуть сами: онлайн школа 8 класс https://shkola-onlajn-55.ru Я если кому интересно ещё раньше вообще относился скептически к таким форматам. Оказалось — реально работает. У них и обратная связь отличная. В общем, рекомендую присмотреться. Удачи!

  1016. syvenirnaya prodykciya s logotipom_lyki

    Коллеги, всем привет! Встала задача обновить ассортимент брендированной атрибуки для отдела продаж. Посоветуйте нормальное изготовление корпоративных сувениров — чтобы и кружки не облазили, и ручки писали. подарок на заказ https://suvenirnaya-produkcziya-s-logotipom-11.ru Реально ли найти недорогую сувенирную продукцию с логотипом с печатью от 100 штук. Может, есть проверенные фабрики, которые работают напрямую, без посредников. Киньте ссылки или названия компаний, буду очень благодарен.

  1017. syvenirnaya prodykciya s logotipom_jgkt

    Народ, привет! Такая ситуация — на планерке сказали срочно найти подарки для клиентов. Присматриваюсь к подаркам с логотипом, но боюсь нарваться на кривую печать. корпоративная продукция с логотипом https://suvenirnaya-produkcziya-s-logotipom-10.ru Кто уже заказывал корпоративные подарки с логотипом компании, поделитесь опытом. Просили ещё брендированные кружки и толстовки. Заранее респект тем, кто откликнется с контактами проверенными.

  1018. skolko stoit yzakonit pereplanirovky_ycpi

    Ребята, привет! Соседи залили, решил сделать ремонт, а там. Поменяли газовую плиту, сдвинули раковину, а стены вообще вынесли — думал, пронесёт. В общем, инспекция пришла и выписала предписание. И тут встал вопрос: перепланировка квартиры стоимость перепланировка квартиры стоимость говорят, согласование перепланировки квартиры цена сильно выросла после ужесточения норм. Плюс эти дурацкие техусловия на вентиляцию. Если кто недавно проходил это ад, поделитесь. Без этого всё равно потом квартиру не продать. Короче, нужна стоимость согласования перепланировки, реальная по рынку.

  1019. Kak naiti cheloveka po nomery telefona_ezer

    Уже отчаялся был найти хоть что-то стоящее. Знакомая многим фигня, нужно срочно проверить один подозрительный номер. Стало дико интересно,. И знаете что? Оказывается, сейчас есть реальные способы.

    Короче, если вас сейчас волнует тот же самый вопрос — как вычислить анонимного абонента, то есть один проверенный временем вариант. Конкретно про то, где найти по телефонному номеру актуальные данные — вот здесь всё максимально норм расписано: адрес по номеру телефона адрес по номеру телефона.

    Друзьям ссылку скинул в телегу, им тоже помогло. Потому что в открытых пабликах обычно полная тишина. В общем, кому надо — тот точно воспользуется. Надеюсь, кому-то тоже упростит жизнь.

  1020. melbet_ilpn

    Давно искал инфу и наконец-то разобрался с этой проблемой. Там всё разложено по полочкам, без лишней воды и тупых SEO-текстов. Сам долго мучился, пока не нашел этот гайд. Вот мелбет казино скачать на андроид мелбет казино скачать на андроид — советую изучить на досуге. Там внутри и примеры, и пошаговые инструкции, короче полный фарш.

  1021. syvenirnaya prodykciya s logotipom_pwki

    Коллеги, всем привет! Организуем встречу с дилерами, хочется сделать им приятные и полезные презенты. Посоветуйте нормальное изготовление корпоративных сувениров — чтобы и кружки не облазили, и ручки писали. корпоративные подарки оптом корпоративные подарки оптом Реально ли найти недорогую сувенирную продукцию с логотипом с печатью от 100 штук. Может, есть проверенные фабрики, которые работают напрямую, без посредников. А то маркетинговые агентства такой ценник лупят — закачаешься.

  1022. shkola onlain_qhOa

    Признаюсь, сначала очень сильно сомневался в этой затее, но после советов хороших знакомых наткнулся на один нормальный человеческий вариант. К слову, вот что я понял: современная онлайн-школа для детей — это не просто унылые вебинарчики. Там и домашние задания с подробной индивидуальной проверкой, что очень радует на практике.

    В общем, кому реально нужно нормальное обучение в теме образовательные онлайн школы — убедитесь во всём сами, вот здесь все выложено без лишней воды: школа дистанционного обучения школа дистанционного обучения.

    А я пока пойду дальше разбираться с расписанием. Потому что обычная школа часто проигрывает по всем фронтам, а тут организована именно живое регулярное общение с кураторами. Пригодится точно, потом еще спасибо скажете.

  1024. syvenirnaya prodykciya s logotipom_xxSn

    Срочно нужен совет тем, кто занимается брендингом. Хотим обновить мерч для сотрудников. Везде говорят про индивидуальный подход, но реально где заказать корпоративные подарки с логотипом компании — чтоб не за границей, но и не откровенный шлак. заказать сувенирную продукцию с логотипом компании https://suvenirnaya-produkcziya-s-logotipom-9.ru Интересует именно изготовление под ключ — от кружек до брендированных блокнотов. Нам нужно от 500 штук, можно меньше. Заранее спасибо, кто откликнется.

  1025. tkan dlya mebeli_iupr

    Если честно, сам перерыл кучу форумов в поисках нормальной обивки. Оказалось, что выбрать подходящий вариант тот ещё квест. Короче, смотрите, вот здесь реально толково расписано про плотность, ворс и износостойкость для диванов и кресел, а главное — показаны варианты, которые не выцветают. Вся полезная информация доступна здесь: ткани для мебели в москве https://tkan-dlya-mebeli-2.ru Дальше сами гляньте примеры в интерьере. Да, и не берите первое, что попалось — я уже поплатился кошельком, когда брал дешёвую ткань для обивки мебели. Эта тема реально вывозит по соотношению цена-качество. Имейте в виду: ткань для обивки мебели купить лучше уже с нормальной пропиткой от грязи. Да и садится такое полотно гораздо меньше. Здесь реально дельные советы.

  1028. tkan dlya mebeli_dukn

    Ребята, выручайте! Решил обновить кухонный уголок, а старую обивку уже не найти. Теперь мучаюсь — какую взять ткань для мебели, чтобы и выглядело достойно, и кошачьи когти выдержало. ткань для мебели купить [url=https://tkan-dlya-mebeli-1.ru]https://tkan-dlya-mebeli-1.ru[/url] А то везде пишут разное, а на деле хочется купить ткань мебельную и забыть на пару лет. Буду благодарен за любые советы, особенно от тех, кто сам перетягивал.

  1029. Kak naiti cheloveka po nomery telefona_zuer

    Уже отчаялся был найти хоть что-то стоящее. Знакомая многим фигня, постоянно звонят с незнакомого телефона, а кто — вообще непонятно. Стало дико интересно,. И знаете что? Не всё так сложно в этом плане, как кажется.

    Короче, если вас сейчас волнует тот же самый вопрос — быстро определить владельца номера, то есть один реально работающий и живой сервис. Конкретно про то, как найти человека по номеру телефона — вот здесь всё максимально норм расписано: вычислить по номеру телефона вычислить по номеру телефона.

    Друзьям ссылку скинул в телегу, им тоже помогло. Потому что обычный поиск гуглит только рекламный спам. В общем, кому надо — тот точно воспользуется. Век живи — век учись, как говорится.

  1030. syvenirnaya prodykciya s logotipom_zkkt

    Народ, привет! Ох, уже голова болит с этим тимбилдингом, нужны нормальные презенты для партнеров. Присматриваюсь к подаркам с логотипом, но боюсь нарваться на кривую печать. подарки с логотипом организации подарки с логотипом организации Говорят, сейчас модно заказывать корпоративные подарки сувениры из экокожи — но кто делает качественно. Просили ещё брендированные кружки и толстовки. Заранее респект тем, кто откликнется с контактами проверенными.

  1031. syvenirnaya prodykciya s logotipom_qhki

    Коллеги, всем привет! Срочно нужна консультация тех, кто уже заказывал мерч для бизнеса. Подскажите, где заказать качественную сувенирную продукцию с логотипом. корпоративные сувениры на заказ корпоративные сувениры на заказ А то насчитали мне за брендированные блокноты космос, хотя заказывали всего 50 позиций. Может, есть проверенные фабрики, которые работают напрямую, без посредников. А то маркетинговые агентства такой ценник лупят — закачаешься.

  1032. melbet_uypn

    Ребят, наконец-то наткнулся на реальный опыт. Авторы реально шарят в вопросе, никаких банальных советов из интернета. Многие на форумах спорят, а ответ лежал на поверхности. Вот мелбет скачать приложение на андроид мелбет скачать приложение на андроид — сохраняйте себе в закладки, пригодится. Мне лично это сэкономило кучу времени и нервов, так что делюсь от души.

  1033. Narkolog na dom_dept

    Знаете, ситуация бывает — близкий совсем плох, а тащить в клинику нет сил. Моя семья такое пережила пару лет назад . Сидишь, не знаешь что делать . Лезешь в интернет, а вокруг сплошной развод . Пока кто-то не подсказал один нормальный проверенный вариант. Требуется немедленная консультация — а ехать куда-то нет возможности , то нужно вызывать врача на дом. Речь конкретно про нарколога на дом . У нас в Самаре, если честно, хватает шарлатанов . Нормальные контакты, кто реально приезжает вот тут : вызвать нарколога на дом цены вызвать нарколога на дом цены Откровенно говоря, после того как вник в детали, многое прояснилось . И про снятие запоя на дому, и про консультацию . Плюс анонимность — это важно . Советую не откладывать.

  1034. Kak naiti cheloveka po nomery telefona_jter

    Случайно наткнулся на один гайд, Прям беда реальная: потерял контакт со старым хорошим другом. Стало дико интересно,. И знаете что? Не всё так сложно в этом плане, как кажется.

    Короче, если вас сейчас волнует тот же самый вопрос — пробить странный входящий звонок, то есть один реально работающий и живой сервис. Конкретно про то, как найти человека по номеру телефона — вот здесь всё максимально норм расписано: пробить номер телефона где находится пробить номер телефона где находится.

    Друзьям ссылку скинул в телегу, им тоже помогло. Потому что обычный поиск гуглит только рекламный спам. В общем, обязательно сохраните себе на будущее. Тема вроде избитая, но толковое решение всё же нашлось.

  1035. syvenirnaya prodykciya s logotipom_gcki

    Коллеги, всем привет! Срочно нужна консультация тех, кто уже заказывал мерч для бизнеса. Посоветуйте нормальное изготовление корпоративных сувениров — чтобы и кружки не облазили, и ручки писали. подарочная сувенирная продукция подарочная сувенирная продукция Где сейчас лучше заказывать корпоративные подарки сувениры — в России или все-таки из Китая везти. Может, есть проверенные фабрики, которые работают напрямую, без посредников. А то маркетинговые агентства такой ценник лупят — закачаешься.

  1036. syvenirnaya prodykciya s logotipom_imkt

    Народ, привет! Ох, уже голова болит с этим тимбилдингом, нужны нормальные презенты для партнеров. Может, кто шарит где лучше брать сувенирную продукцию с логотипом. купить корпоративные подарки с логотипом https://suvenirnaya-produkcziya-s-logotipom-10.ru Посоветуйте нормального поставщика сувенирной продукции с логотипом, чтобы не обдиралово было. Просили ещё брендированные кружки и толстовки. Заранее респект тем, кто откликнется с контактами проверенными.

  1037. tkan dlya mebeli_ippr

    Если честно, сам перерыл кучу форумов в поисках нормальной обивки. Оказалось, что выбрать подходящий вариант реальная проблема. Итак, смотрите, вот здесь реально толково расписано про плотность, ворс и износостойкость для диванов и кресел, а главное — показаны варианты, которые легко чистить. Вся полезная информация доступна здесь: купить мебельную ткань в москве в розницу купить мебельную ткань в москве в розницу Дальше сами гляньте фактические отзывы. Да, и не берите первое, что попалось — я уже сделал ошибку, когда брал ткань для мебели на распродаже. Эта тема реально вывозит по износу. Имейте в виду: ткань мебельная купить лучше уже с нормальной пропиткой от грязи. Да и трётся такое полотно гораздо меньше. Не поленитесь, откройте.

  1038. skolko stoit yzakonit pereplanirovky_wppi

    Ребята, привет! Я вообще в шоке, если честно. Акт скрытых работ потерял, да и проект сам переделывал. В общем, теперь легализовывать этот бардак придётся официально. И тут встал вопрос: согласование перепланировки квартиры цена согласование перепланировки квартиры цена просто интересно, стоимость согласования перепланировки квартиры сейчас вообще реальная или грабёж. Плюс эти дурацкие техусловия на вентиляцию. Если кто недавно проходил это ад, поделитесь. Без этого а если решите ипотеку рефинансировать, БТИ зарубит. Короче, просто сколько отдать, чтобы спать спокойно с новой планировкой.

  1039. syvenirnaya prodykciya s logotipom_paSn

    Срочно нужен совет для отдела маркетинга. Планируем раздачу для партнёров на новый год. Везде говорят про индивидуальный подход, но реально найти нормальную сувенирную продукцию с логотипом. сувенирная продукция с логотипом цена https://suvenirnaya-produkcziya-s-logotipom-9.ru Интересует именно изготовление под ключ — от кружек до брендированных блокнотов. Нам нужно от 500 штук, можно меньше. А то бюджет уже вчера утвердили, а поставщика нет.

  1040. Narkologicheskii stacionar_ezPa

    Вот такой момент: подбор качественного стационара — это всегда целая проблема и головная боль. Нередко в жизни бывает так, когда родным или близким людям срочно понадобилась грамотная помощь врачей. И в этот момент обычно начинается паника просто из-за банальной нехватки информации.

    Я сам недавно детально изучал этот вопрос, искал по-настоящему работающий и безопасный выход. В интернете сейчас столько мусора и дорвеев, что голова идет кругом. Короче говоря, советую присмотреться к одному источнику, там подробно расписаны все важные условия и нюансы про круглосуточную наркологическую поддержку и условия проживания. В такой ситуации лучше один раз внимательно глянуть самостоятельно, чтобы четко во всем разобраться.

    Все важные детали и лицензии центра находятся только тут: наркологические стационары narkologicheskij-staczionar-sankt-peterburg-12.ru. Сам сначала даже не думал, насколько там много подводных камней, на которые стоит обращать внимание, включая комфортные условия содержания, современные палаты и полную анонимность. Для Санкт-Петербурга это точно один из самых лучших вариантов, который стабильно работает и имеет хорошие отзывы.

  1041. syvenirnaya prodykciya s logotipom_ojkt

    Народ, привет! Такая ситуация — на планерке сказали срочно найти подарки для клиентов. Присматриваюсь к подаркам с логотипом, но боюсь нарваться на кривую печать. сувениры и подарки с логотипом https://suvenirnaya-produkcziya-s-logotipom-10.ru Кто уже заказывал корпоративные подарки с логотипом компании, поделитесь опытом. Просили ещё брендированные кружки и толстовки. Заранее респект тем, кто откликнется с контактами проверенными.

  1042. Armandocip

    Нашел место, где можно раздобыть свежие промокоды на монеты и попасть на оригинальную платформу. Для тех, кому важен настоящий Dragon Money и его честные выплаты, следуйте по прямой ссылке. Драгон Мани официальный

  1043. RonaldzeX

    Из-за блокировок провайдера пришлось искать новый домен, чтобы играть без задержек. Рабочую ссылку на Dragon Money я нашел вот в этом источнике: Dragon Money зеркало

  1044. Narkolog na dom_xgPn

    Слушайте, какая история — родственник в тяжелом запое , а тащить в больницу просто нереально . Моя семья такое пережила недавно совсем. Сидишь, не знаешь за что хвататься . Лезешь в интернет, а вокруг сплошной развод . Пока случайно не нашел один реально работающий вариант. Если нужна срочная помощь — а везти самому просто нереально, то нужно вызывать врача на дом. Я про нарколога на дом . В Самаре , если честно, тоже полно левых контор без лицензии. Вся проверенная информация вот тут : нарколог самара https://narkolog-na-dom-samara-14.ru Откровенно говоря, после того как вник в детали, понял, как правильно действовать. Там и про капельницы подробно , и про последующее кодирование. И цены адекватные, без разводов. Рекомендую не тянуть .

  1045. Andrewjah

    Do you love excitement? https://jerseysbeststore.com/glossary offers premium pre-match and live sports betting, as well as a legal online casino. Try your luck on modern slots, table games, or with live dealers. We guarantee complete data security, fair results, and 24/7 player support.

  1046. tkan dlya mebeli_zqpr

    Если честно, сам перерыл кучу форумов в поисках нормальной мебельной ткани. Оказалось, что выбрать подходящий вариант тот ещё квест. Короче, смотрите, вот здесь реально толково расписано про плотность, ворс и износостойкость для диванов и кресел, а главное — показаны варианты, которые легко чистить. Вся полезная информация доступна здесь: мебельные ткани цены https://tkan-dlya-mebeli-2.ru Дальше сами гляньте примеры в интерьере. Да, и не берите первое, что попалось — я уже поплатился кошельком, когда брал мебельную ткань купить с рук. Эта тема реально вывозит по износу. Кстати: ткань для обивки мебели купить лучше уже с нормальной пропиткой от грязи. Да и рвётся такое полотно гораздо меньше. Здесь реально дельные советы.

  1047. luxury car rental miami_ppoa

    Let’s be real, finding a decent rental company down here is a nightmare. Or worse — they freeze your credit card for an extra two grand and smile like it’s totally normal. Fool me once, shame on you, right. When you are trying to find a reliable premium fleet down here, make sure to check the actual fleet reviews before signing anything. Miami without a decent whip is pretty rough, especially if you want ice-cold AC and no ridiculous daily mileage caps.

    I’ve literally compared maybe 15 different local providers last month alone, until I finally stumbled across one that actually delivers what it promises. If you are looking for an honest source for premium rentals across Florida, check the details here: luxury car rental miami fl luxury car rental miami fl. Yeah, finding parking in downtown is still its own separate nightmare, but that’s on you. Just drive safe out there and don’t let them upsell you on unnecessary insurance nonsense. hope this helps someone save a few bucks.

  1048. Narkologicheskii stacionar_brPa

    Знаете, поиск действительно проверенного медицинского центра — это реально отдельная и очень сложная история. Нередко в жизни бывает так, когда кому-то из членов семьи срочно понадобилась грамотная помощь врачей. И тут сразу возникает главный вопрос: куда именно везти человека?

    Мой коллега по работе долго искал действительно надежный медицинский вариант. В интернете сейчас столько мусора и дорвеев, что голова идет кругом. Если коротко, лучше сразу перейти на официальный сайт, где нет вранья, там действительно раскладывают по полочкам всю подноготную про анонимное снятие запоя в условиях клиники. В общем, не тяните время и долго не раздумывайте,, чтобы четко во всем разобраться.

    Вся актуальная информация и контакты доступны прямо здесь: наркология стационар http://www.narkologicheskij-staczionar-sankt-peterburg-12.ru. Сам сначала даже не думал, насколько там много подводных камней, на которые стоит обращать внимание, и главное — там работают доктора, которые реально спасают людей. Для Санкт-Петербурга это точно один из самых лучших вариантов, так что рекомендую сохранить себе в закладки на всякий случай.

  1049. Narkolog na dom_djPn

    Знаете, бывает такое — человек в ступоре , а тащить в больницу страшно . Моя семья такое пережила недавно совсем. Сидишь, не знаешь за что хвататься . Лезешь в интернет, а вокруг сплошной развод . Пока кто-то не подсказал один нормальный проверенный вариант. Если нужна срочная помощь — а ехать куда-то просто нереально, то выход один . Речь конкретно про выезд нарколога на дом. В Самаре , к слову , хватает шарлатанов . Нормальные контакты, кто реально приезжает вот тут : нарколог самара https://narkolog-na-dom-samara-14.ru Откровенно говоря, после того как прочитал , понял, как правильно действовать. И про снятие запоя на дому, и про последующее кодирование. И цены адекватные, без разводов. Советую не откладывать.

  1050. Narkolog na dom_ywpt

    Случается, когда уже не до раздумий — близкий совсем плох, а тащить в клинику нет сил. Я сам через это прошёл пару лет назад . Руки опускаются, время идёт. Начинаешь обзванивать знакомых , а вокруг одни обещания . Пока кто-то не подсказал один реально работающий вариант. Если нужна срочная помощь — а ехать куда-то нет возможности , то выход один . Я про нарколога на дом . У нас в Самаре, если честно, хватает левых контор без лицензии. Вся проверенная информация вот тут : нарколог домой нарколог домой Честно скажу , после того как прочитал , понял, как правильно действовать. Там и про капельницы подробно , и про последующее кодирование. Плюс анонимность — это важно . Советую не откладывать.

  1052. syvenirnaya prodykciya s logotipom_kxSn

    Срочно нужен совет кто уже заказывал партию к выставке. Готовимся к конференции. Везде говорят про индивидуальный подход, но реально где заказать корпоративные подарки с логотипом компании — чтоб не за границей, но и не откровенный шлак. подарки с логотипом подарки с логотипом Кто недавно заморачивался подарками с логотипом, поделитесь контактами. Пока просто собираем инфу. А то бюджет уже вчера утвердили, а поставщика нет.

  1053. Kurtisdardy

    Do you love excitement? https://jerseysbeststore.com/glossary offers premium pre-match and live sports betting, as well as a legal online casino. Try your luck on modern slots, table games, or with live dealers. We guarantee complete data security, fair results, and 24/7 player support.

  1054. luxury car rental miami_evoa

    Let’s be real, finding a decent rental company down here is a nightmare. Or worse — they freeze your credit card for an extra two grand and smile like it’s totally normal. Fool me once, shame on you, right. If you actually need a proper vehicle to cruise around the city, make sure to check the actual fleet reviews before signing anything. Miami without a decent whip is pretty rough, whether you are heading to Brickell, Coconut Grove, or just driving down to Key Biscayne.

    I’ve literally compared maybe 15 different local providers last month alone, until I finally stumbled across one that actually delivers what it promises. If you are looking for an honest source for premium rentals across Florida, check the details here: miami south beach rental cars https://luxury-car-rental-miami-2.com. Yeah, finding parking in downtown is still its own separate nightmare, but that’s on you. Just drive safe out there and don’t let them upsell you on unnecessary insurance nonsense. hope this helps someone save a few bucks.

  1055. Narkolog na dom_kbPn

    Вот реально ситуация — близкий совсем плох, а везти в клинику страшно . Я сам через это прошел пару лет назад . Сидишь, не знаешь за что хвататься . Лезешь в интернет, а вокруг сплошной развод . Пока случайно не нашел один реально работающий вариант. Если нужна немедленная консультация — а ехать куда-то просто нереально, то выход один . Я про наркологическую помощь на дому . У нас в Самаре, если честно, тоже полно левых контор без лицензии. Нормальные контакты, кто реально приезжает вот тут : вызов нарколога на дом круглосуточно недорого https://narkolog-na-dom-samara-14.ru Откровенно говоря, после того как вник в детали, многое прояснилось . И про снятие запоя на дому, и про последующее кодирование. Плюс анонимность — это важно . Рекомендую не откладывать.

  1056. Narkologicheskii stacionar_eiPa

    Слушайте, а вы в курсе, что найти нормальную клинику сейчас — это реально отдельная и очень сложная история. Многие лично сталкивались с такой ситуацией,, когда кому-то из членов семьи внезапно потребовалась экстренная и профессиональная поддержка. И тут сразу возникает главный вопрос: куда именно везти человека?

    Я сам недавно детально изучал этот вопрос, искал действительно надежный медицинский вариант. В интернете сейчас столько мусора и дорвеев, что голова идет кругом. Короче говоря, советую присмотреться к одному источнику, там подробно расписаны все важные условия и нюансы про круглосуточную наркологическую поддержку и условия проживания. В общем, не тяните время и долго не раздумывайте,, чтобы четко во всем разобраться.

    Вся актуальная информация и контакты доступны прямо здесь: лечение запоя в стационаре санкт петербург лечение запоя в стационаре санкт петербург. Честно говоря, после изучения всех условий, насколько там много полезных нюансов и скрытых факторов, и главное — там работают доктора, которые реально спасают людей. В Питере это определенно достойный внимания и доверия медицинский центр, который стабильно работает и имеет хорошие отзывы.

  1058. Narkolog na dom_fipt

    Знаете, ситуация бывает — близкий совсем плох, а везти в больницу страшно . Я сам через это прошёл недавно. Сидишь, не знаешь что делать . Лезешь в интернет, а вокруг бабло тянут. Пока случайно не наткнулся на один реально работающий вариант. Требуется немедленная консультация — а ехать куда-то просто нереально, то нужно вызывать врача на дом. Речь конкретно про наркологическую помощь на дому . В Самаре , к слову , тоже полно шарлатанов . Нормальные контакты, кто реально приезжает вот тут : помощь нарколога на дому помощь нарколога на дому Откровенно говоря, после того как вник в детали, понял, как правильно действовать. И про снятие запоя на дому, и про последующее кодирование. Плюс анонимность — это важно . Рекомендую не тянуть .

  1061. tkan dlya mebeli_aapr

    Если честно, сам перерыл кучу форумов в поисках нормальной ткани для мебели. Оказалось, что выбрать подходящий вариант совсем непросто. В общем, смотрите, вот здесь реально толково расписано про плотность, ворс и износостойкость для диванов и кресел, а главное — показаны варианты, которые легко чистить. Вся полезная информация доступна здесь: материал для обтяжки дивана https://tkan-dlya-mebeli-2.ru Дальше сами гляньте фактические отзывы. Да, и не берите первое, что попалось — я уже обжёгся, когда брал дешёвую ткань для обивки мебели. Эта тема реально вывозит по качеству. Имейте в виду: ткань мебельная купить лучше уже с нормальной пропиткой от грязи. Да и садится такое полотно гораздо меньше. Не поленитесь, откройте.

  1068. luxury car rental miami_yfoa

    Honestly, I’ve wasted so much time on sketchy rental deals around South Beach. You book a premium ride online, show up, and they hand you keys to something with a dented bumper. Fool me once, shame on you, right. If you actually need a proper vehicle to cruise around the city, seriously, do your homework first and don’t just trust social media ads. Miami without a decent whip is pretty rough, especially if you want ice-cold AC and no ridiculous daily mileage caps.

    Most of these local agencies are just fancy websites hiding a garbage fleet, but I eventually found a service with zero hidden fees and no bait-and-switch tactics. If you are looking for an honest source for premium rentals across Florida, check the details here: car rentals miami https://luxury-car-rental-miami-2.com. Yeah, finding parking in downtown is still its own separate nightmare, but that’s on you. Just drive safe out there and don’t let them upsell you on unnecessary insurance nonsense. let me know if you guys know any other clean spots.

  1069. melbet_yvKn

    Слушайте, кто в курсе, долго сомневался до последнего, но на прошлой неделе таки зарегился ради интереса в mel bet. Честно? Зашло прям на ура,. Особенно если вам надо скачать melbet на андроид — у меня смартфон далеко не новый,, но никаких тормозов вообще нет.

    В общем, гляньте сами все условия по ссылке: мелбет казино скачать мелбет казино скачать. Кстати, кто спрашивал про мелбет приложение — там есть удобный отдельный раздел,. И фрибеты для новичков очень приятные,. Я лично всё проверял на себе — выплаты приходят максимально быстрые, Очень рекомендую этот вариант. Удачи всем!

  1070. melbet_hhml

    Давно хотел найти надёжный вариант, честно говоря, перепробовал кучу сомнительных контор. Но на днях близкий друг посоветовал про melbet. Решил не полениться и затестить — и очень даже зашло,.

    В общем, вся нужная инфа доступна вот тут: melbet скачать казино melbet скачать казино. Кстати, если кому надо скачать мелбет — там нет никаких лишних телодвижений. Я себе установил софт прямо на телефон — полёт отличный. И вывод денег действительно шустрый, В общем, рекомендую присмотреться. Удачи всем на дистанции!

  1072. Narkolog na dom_kpPn

    Вот реально ситуация — человек в ступоре , а везти в клинику страшно . Я сам через это прошел недавно совсем. Сидишь, не знаешь за что хвататься . Лезешь в интернет, а вокруг одни обещания . Пока кто-то не подсказал один реально работающий вариант. Требуется срочная помощь — а везти самому нет физической возможности , то выход один . Речь конкретно про круглосуточный вызов нарколога . У нас в Самаре, к слову , хватает шарлатанов . Нормальные контакты, кто реально приезжает ниже по ссылке: заказать нарколога https://narkolog-na-dom-samara-14.ru Откровенно говоря, после того как прочитал , многое прояснилось . Там и про капельницы подробно , и про консультацию нарколога . Плюс анонимность — это важно . Рекомендую не откладывать.

  1073. vivod iz zapoya v stacionare_dlPr

    Знаете ситуацию выматывает , когда родственник просто не может остановиться . Ломаешь голову , а вокруг одна потёмки . Знакомому потребовался срочный выход . Пьют успокоительное , но это ерунда . Нужно именно профессиональная помощь . Пролистал пол-интернета , пока понял одну простую вещь: без нормальных условий ничего не выйдет . Потому что дома срыв стопроцентный . Если ищешь где сделать вывода из запоя в стационаре — тогда тебе сюда . В Нижнем , кстати, развелось этих «центров» . Советую перейти на сайт, где реально раскладывают по полочкам про кодировку от алкоголя и работу нарколога . Подробности по ссылке: психиатр нарколог нижний новгород психиатр нарколог нижний новгород После прочтения , сам офигел , сколько нюансов в этой теме. И кстати, цены адекватные. Для нашего города это реально стоящий вариант.

  1074. melbet_nfmr

    Народ, привет! долго откладывал этот момент до последнего, но вчера все-таки попробовал сделать пару ставок в mel bet. Скажу так — очень зашло с первых минут,. У кого система ios — всё четко и стабильно работает. Надо melbet скачать ios? За пять минут софт поставил на смарт,.

    Короче, вся полезная инфа и актуальный сайт доступны вот тут: . Кстати, кто спрашивал про скачать мелбет казино — мобильная версия работает без лагов,. И вывод средств действительно быстрый. Я за месяц три раза выигрыш забирал — всё честно и без обмана. Сам теперь только туда захожу. Пользуйтесь на здоровье, пусть повезет!

  1078. Narkolog na dom_bdpt

    Знаете, ситуация бывает — человек в ступоре , а везти в больницу просто нереально . Моя семья такое пережила пару лет назад . Сидишь, не знаешь что делать . Лезешь в интернет, а вокруг одни обещания . Пока кто-то не подсказал один реально работающий вариант. Если нужна срочная помощь — а везти самому нет возможности , то выход один . Речь конкретно про круглосуточный выезд нарколога. В Самаре , если честно, хватает левых контор без лицензии. Нормальные контакты, кто реально приезжает вот тут : нарколог на дом круглосуточно цены [url=https://narkolog-na-dom-samara-13.ru]нарколог на дом круглосуточно цены[/url] Откровенно говоря, после того как прочитал , понял, как правильно действовать. Там и про капельницы подробно , и про консультацию . Плюс анонимность — это важно . Рекомендую не тянуть .

  1079. magazin premialnih tovarov_sxSi

    Мужики, привет. Долго сомневался, где найти что-то реально редкое. Перерыл кучу сайтов, но нормального магазина премиальных товаров — днём с огнём не сыщешь. А тут по совету зашёл. В общем, сам гляньте по ссылке: магазин премиальных брендов [url=https://boutique-guide.ru]магазин премиальных брендов[/url] Кстати, если ищете премиальные подарки для мужчин — там есть даже редкие позиции. Я себе взял кожаную сумку — качество бомба. И цены адекватные для такого уровня. Лучший вариант для эксклюзива. Надеюсь, поможет.

  1080. luxury car rental miami_uxMn

    Okay so here’s the deal with renting anything decent in Miami. I swear half the «luxury» fleets down here are straight-up marketing scams. You book a premium ride online, arrive all excited, then boom — hidden service fees everywhere. Fool me thrice, shame on both of us I guess, lesson learned. When you are trying to find a reliable premium fleet down here, do some real digging first and read actual customer reviews. Miami without wheels is basically a hostage situation, whether you are doing Brickell mornings, South Beach nights, or a spontaneous Keys trip.

    I literally spent last month comparing maybe twenty different companies, until I finally found one outfit that actually delivers what’s in the photos. If you are looking for the only straight shooter for premium rentals across South Florida, check the details here: rent a sedan car [url=https://luxury-car-rental-miami-3.com]https://luxury-car-rental-miami-3.com[/url]. Also, definitely bring sunglasses unless you enjoy driving completely blind in that sun. Just drive safe out there and maybe skip the extra windshield protection thing. hope this helps some of you save a few bucks.

  1081. Narkologicheskii stacionar_xuPa

    Вот такой момент: подбор качественного стационара — это всегда целая проблема и головная боль. Нередко в жизни бывает так, когда кому-то из членов семьи срочно понадобилась грамотная помощь врачей. И в этот момент обычно начинается паника просто из-за банальной нехватки информации.

    Мой коллега по работе долго искал действительно надежный медицинский вариант. Очень сложно с ходу отличить реальные отзывы пациентов от банальной рекламы. Короче говоря, советую присмотреться к одному источнику, там действительно раскладывают по полочкам всю подноготную про анонимное снятие запоя в условиях клиники. В такой ситуации лучше один раз внимательно глянуть самостоятельно, чтобы четко во всем разобраться.

    Все важные детали и лицензии центра находятся только тут: выведение из запоя в стационаре спб [url=https://narkologicheskij-staczionar-sankt-peterburg-12.ru]https://narkologicheskij-staczionar-sankt-peterburg-12.ru[/url]. Честно говоря, после изучения всех условий, насколько там много подводных камней, на которые стоит обращать внимание, и главное — там работают доктора, которые реально спасают людей. Для Санкт-Петербурга это точно один из самых лучших вариантов, который стабильно работает и имеет хорошие отзывы.

  1082. melbet_asKn

    Ребята, всем привет! долго сомневался до последнего, но на прошлой неделе таки решил глянуть в mel bet. Честно? Остался полностью доволен,. Особенно если вам надо скачать мелбет на андроид — у меня телефон не флагман,, но никаких тормозов вообще нет.

    В общем, убедитесь сами, если перейдете: мелбет скачать казино [url=https://v-bux.ru]https://v-bux.ru[/url]. Кстати, кто спрашивал про мелбет приложение — там установочный файл чистый и без вирусов. И фрибеты для новичков очень приятные,. Я уже выводил выигранные средства — никаких проблем с этим нет, Сам теперь только туда. Удачи всем!

  1083. melbet_drml

    Давно искал, где можно нормально играть, честно говоря, много где в итоге разочаровался. Но на днях близкий друг посоветовал про mel bet. Решил лично проверить систему — и ни разу не пожалел,.

    В общем, сами гляньте все условия по ссылке: скачат мелбет [url=https://iamthecoffeechic.com]https://iamthecoffeechic.com[/url]. Кстати, если кому надо скачать melbet — там нет никаких лишних телодвижений. Я себе поставил официальное приложение — никаких тормозов нет. И бонусы на первый депозит приятные, Доволен как слон, честно говоря. Удачи всем на дистанции!

  1084. luxury car rental miami_bdoa

    Honestly, I’ve wasted so much time on sketchy rental deals around South Beach. You book a premium ride online, show up, and they hand you keys to something with a dented bumper. Fool me once, shame on you, right. When you are trying to find a reliable premium fleet down here, seriously, do your homework first and don’t just trust social media ads. Everyone who lives here knows that having a solid car is essential, especially if you want ice-cold AC and no ridiculous daily mileage caps.

    I’ve literally compared maybe 15 different local providers last month alone, until I finally stumbled across one that actually delivers what it promises. If you are looking for an honest source for premium rentals across Florida, check the details here: porsche 911 carrera for rent near me [url=https://luxury-car-rental-miami-2.com]https://luxury-car-rental-miami-2.com[/url]. Yeah, finding parking in downtown is still its own separate nightmare, but that’s on you. Just drive safe out there and don’t let them upsell you on unnecessary insurance nonsense. let me know if you guys know any other clean spots.

  1085. Narkolog na dom_gcPn

    Вот реально ситуация — человек в ступоре , а везти в клинику нет никаких сил. Моя семья такое пережила недавно совсем. Руки опускаются, время тикает. Лезешь в интернет, а вокруг одни обещания . Пока кто-то не подсказал один нормальный проверенный вариант. Если нужна срочная помощь — а ехать куда-то нет физической возможности , то выход один . Речь конкретно про нарколога на дом . У нас в Самаре, если честно, тоже полно левых контор без лицензии. Нормальные контакты, кто реально приезжает вот тут : частный нарколог [url=https://narkolog-na-dom-samara-14.ru]https://narkolog-na-dom-samara-14.ru[/url] Честно скажу , после того как прочитал , многое прояснилось . Там и про капельницы подробно , и про последующее кодирование. Плюс анонимность — это важно . Советую не откладывать.

  1086. tkan dlya mebeli_wepr

    Если честно, сам перерыл кучу форумов в поисках нормальной мебельной ткани. Оказалось, что выбрать подходящий вариант совсем непросто. В общем, смотрите, вот здесь реально толково расписано про плотность, ворс и износостойкость для диванов и кресел, а главное — показаны варианты, которые легко чистить. Вся полезная информация доступна здесь: обивочные ткани для мягкой мебели [url=https://tkan-dlya-mebeli-2.ru]обивочные ткани для мягкой мебели[/url] Дальше сами гляньте каталог с ценами. Да, и не берите первое, что попалось — я уже поплатился кошельком, когда брал ткань для мебели на распродаже. Эта тема реально вывозит по износу. Для информации: ткань мебельная купить лучше уже с нормальной пропиткой от грязи. Да и рвётся такое полотно гораздо меньше. Не поленитесь, откройте.

  1087. vivod iz zapoya v stacionare_zfPr

    Знаете ситуацию выматывает , когда близкий просто не может остановиться . Ломаешь голову , а вокруг одна реклама . Знакомому потребовался срочный выход . Пьют успокоительное , но это ерунда . Нужно именно профессиональная помощь . Я перелопатил кучу сайтов , пока понял одну простую вещь: без нормальных условий ничего не выйдет . Потому что дома срыв стопроцентный . Если ищешь где сделать вывода из запоя в стационаре — обрати внимание на один проверенный вариант . В Нижнем , кстати, тоже полно шарлатанов . Советую перейти на сайт, где нет вранья про кодировку от алкоголя и выезд врача . Вся суть здесь: наркология нижний новгород [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-22.ru]наркология нижний новгород[/url] Честно скажу , сам офигел , сколько нюансов в этой теме. Главное — анонимность и палаты. Для нашего города это проверенный временем вариант.

  1089. melbet_romr

    Слушайте, кто шарит, долго присматривался к разным платформам, но на днях все-таки начал пользоваться сервисом в mel bet. Скажу так — залетел нормально и без проблем,. У кого новый айфон — всё четко и стабильно работает. Надо скачать мелбет на айфон? В интерфейсе даже ребёнок разберётся.

    Короче, переходите, точно не пожалеете: . Кстати, кто спрашивал про мелбет скачать приложение — приложение вообще не вылетает,. И бонусы для новичков норм дают,. Я уже выводил пару раз выигранные деньги — никаких косяков с выплатами нет,. Всем искренне рекомендую. Удачи всем!

  1090. luxury car rental miami_suMn

    Let me save you some headache I learned the hard way. I swear half the «luxury» fleets down here are straight-up marketing scams. Oh, and that pretty security deposit? Yeah, good luck getting that money back fast. I’ve been burned like three times already this year alone. If you seriously need a legit vehicle to cruise around the city, don’t just trust the first sponsored ad on social media. Anyone who lives here will tell you the exact same thing, especially since the AC must be arctic and you want zero mileage games.

    I literally spent last month comparing maybe twenty different companies, but I eventually found a service with no bait, no switch, and no weird fine print. If you are looking for the only straight shooter for premium rentals across South Florida, check the details here: luxury car for rent [url=https://luxury-car-rental-miami-3.com]luxury car for rent[/url]. Also, definitely bring sunglasses unless you enjoy driving completely blind in that sun. Anyway, glad there’s at least one honest rental joint left in this town, hope this helps some of you save a few bucks.

  1092. magazin premialnih tovarov_fmSi

    Народ, всем здравствуйте. Долго выбирал, где найти презент, который запомнят. Перерыл кучу вариантов, но нормального премиального интернет магазина — днём с огнём не сыщешь. А тут по совету зашёл. В общем, рекомендую посмотреть: премиальный интернет магазин [url=https://boutique-guide.ru]премиальный интернет магазин[/url] Кстати, если ищете премиум подарки — там есть даже редкие позиции. Я себе взял кожаную сумку — упаковка люкс. И цены адекватные для такого уровня. Сам теперь только там беру. Надеюсь, поможет.

  1094. vivod iz zapoya v stacionare_iePr

    Вот такая тема достала уже , когда человек просто не может остановиться . Ломаешь голову , а вокруг одна реклама . Мне вот потребовался срочный выход . Пьют успокоительное , но это не помогает . Требуется именно врачебное вмешательство . Пролистал пол-интернета , пока понял одну простую вещь: без круглосуточного наблюдения ничего не выйдет . Потому что дома срыв гарантирован . Если ищешь где сделать экстренного вывода из запоя под капельницами — тогда тебе сюда . В Нижнем Новгороде , кстати, тоже полно шарлатанов . Лучше сразу перейти на сайт, где реально раскладывают по полочкам про кодирование от алкоголизма и выезд врача . Вся суть здесь: наркологическая клиника нижний новгород [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-22.ru]наркологическая клиника нижний новгород[/url] После прочтения , сам офигел , сколько подводных камней в этой теме. И кстати, цены адекватные. Для нашего города это проверенный временем вариант.

  1097. melbet_atKn

    Люди, подскажите, долго выбирал нормальную платформу, но в выходные таки решил глянуть в mel bet. Честно? Остался полностью доволен,. Особенно если вам надо скачать мелбет на андроид — у меня смартфон далеко не новый,, но софт реально летает.

    В общем, все подробности и рабочая ссылка доступны вот тут: мелбет скачать приложение [url=https://v-bux.ru]мелбет скачать приложение[/url]. Кстати, кто спрашивал про мелбет приложение — там установочный файл чистый и без вирусов. И кешбек на баланс регулярно капает. Я за месяц три раза деньги забирал — служба поддержки вообще не тупит. Очень рекомендую этот вариант. Дерзайте, пусть повезет!

  1098. melbet_xhml

    Давно присматривался к разным платформам, честно говоря, много где в итоге разочаровался. Но на днях близкий друг посоветовал про melbet. Решил лично проверить систему — и ни разу не пожалел,.

    В общем, все подробности выложены здесь: мелбет [url=https://iamthecoffeechic.com]мелбет[/url]. Кстати, если кому надо скачать melbet — там всё работает стабильно и без глюков. Я себе скачал чистую версию для андроида — всё сделано очень удобно. И вывод денег действительно шустрый, Доволен как слон, честно говоря. Надеюсь, эта рекомендация кому-то пригодится.

  1099. Narkolog na dom_obpt

    Вот такая беда — близкий совсем плох, а тащить в клинику просто нереально . Моя семья такое пережила недавно. Руки опускаются, время идёт. Начинаешь обзванивать знакомых , а вокруг одни обещания . Пока кто-то не подсказал один реально работающий вариант. Если нужна немедленная консультация — а ехать куда-то нет возможности , то нужно вызывать врача на дом. Я про круглосуточный выезд нарколога. В Самаре , к слову , тоже полно левых контор без лицензии. Нормальные контакты, кто реально приезжает вот тут : вызов нарколога на дом недорого [url=https://narkolog-na-dom-samara-13.ru]https://narkolog-na-dom-samara-13.ru[/url] Откровенно говоря, после того как прочитал , многое прояснилось . Там и про капельницы подробно , и про последующее кодирование. И цены адекватные, без разводов. Рекомендую не откладывать.

  1100. luxury car rental miami_qxoa

    Look, I’ve been around the block with these Miami car rentals. You book a premium ride online, show up, and they hand you keys to something with a dented bumper. No thanks, I am completely done with that circus. When you are trying to find a reliable premium fleet down here, make sure to check the actual fleet reviews before signing anything. Miami without a decent whip is pretty rough, especially if you want ice-cold AC and no ridiculous daily mileage caps.

    Most of these local agencies are just fancy websites hiding a garbage fleet, but I eventually found a service with zero hidden fees and no bait-and-switch tactics. If you are looking for an honest source for premium rentals across Florida, check the details here: porsche for rent near me [url=https://luxury-car-rental-miami-2.com]https://luxury-car-rental-miami-2.com[/url]. Oh, and definitely bring polarized sunglasses, because that Florida sun is absolutely no joke. Anyway, at least there’s one trustworthy service left in this town, let me know if you guys know any other clean spots.

  1102. Narkologicheskii stacionar_ghPa

    Вот такой момент: подбор качественного стационара — это всегда целая проблема и головная боль. Нередко в жизни бывает так, когда родным или близким людям внезапно потребовалась экстренная и профессиональная поддержка. И в этот момент обычно начинается паника просто из-за банальной нехватки информации.

    Я сам недавно детально изучал этот вопрос, искал действительно надежный медицинский вариант. Очень сложно с ходу отличить реальные отзывы пациентов от банальной рекламы. Короче говоря, советую присмотреться к одному источнику, там подробно расписаны все важные условия и нюансы про круглосуточную наркологическую поддержку и условия проживания. В общем, не тяните время и долго не раздумывайте,, чтобы четко во всем разобраться.

    Все важные детали и лицензии центра находятся только тут: выведение из запоя в стационаре спб [url=https://narkologicheskij-staczionar-sankt-peterburg-12.ru]https://narkologicheskij-staczionar-sankt-peterburg-12.ru[/url]. Честно говоря, после изучения всех условий, насколько там много подводных камней, на которые стоит обращать внимание, и главное — там работают доктора, которые реально спасают людей. Для Санкт-Петербурга это точно один из самых лучших вариантов, так что рекомендую сохранить себе в закладки на всякий случай.

  1103. Donalddounc

    франшизы кофеен Продажа бизнеса: спрос — это то, что нужно анализировать постоянно, чтобы понять, какой бизнес наиболее ликвидный и востребованный на рынке сегодня. Если вы строите компанию, которая решает реальные проблемы людей, спрос на покупку вашего актива будет всегда расти. Полезность — это товар.

  1106. luxury car rental miami_njMn

    Finding a proper ride in this city is a serious challenge. Half these local companies promise a custom Porsche and hand you a basic sedan with fake leather. Oh, and that pretty security deposit? Yeah, good luck getting that money back fast. Fool me thrice, shame on both of us I guess, lesson learned. When you are trying to find a reliable premium fleet down here, don’t just trust the first sponsored ad on social media. Anyone who lives here will tell you the exact same thing, whether you are doing Brickell mornings, South Beach nights, or a spontaneous Keys trip.

    Most of these local agencies are just shiny websites hiding the same overpriced junk, until I finally found one outfit that actually delivers what’s in the photos. If you are looking for the only straight shooter for premium rentals across South Florida, check the details here: luxury cars to rent near me [url=https://luxury-car-rental-miami-3.com]luxury cars to rent near me[/url]. Also, definitely bring sunglasses unless you enjoy driving completely blind in that sun. Anyway, glad there’s at least one honest rental joint left in this town, hope this helps some of you save a few bucks.

  1108. melbet_nfmr

    Народ, привет! долго откладывал этот момент до последнего, но вчера все-таки зарегился ради интереса в melbet. Скажу так — очень зашло с первых минут,. У кого новый айфон — тоже всё без проблем запускается,. Надо melbet скачать на андроид? В интерфейсе даже ребёнок разберётся.

    Короче, вся полезная инфа и актуальный сайт доступны вот тут: . Кстати, кто спрашивал про скачать мелбет казино — мобильная версия работает без лагов,. И бонусы для новичков норм дают,. Я за месяц три раза выигрыш забирал — никаких косяков с выплатами нет,. Это лучшее, что я пробовал из подобного. Пользуйтесь на здоровье, пусть повезет!

  1109. melbet_cwKn

    Люди, подскажите, долго сомневался до последнего, но недавно таки попробовал сделать пару ставок в melbet. Честно? теперь постоянно туда захожу. Особенно если вам надо мелбет скачать на андроид — у меня смартфон далеко не новый,, но приложение работает плавно.

    В общем, гляньте сами все условия по ссылке: мелбет казино скачать [url=https://v-bux.ru]мелбет казино скачать[/url]. Кстати, кто спрашивал про мелбет казино скачать на андроид — там установочный файл чистый и без вирусов. И кешбек на баланс регулярно капает. Я уже выводил выигранные средства — никаких проблем с этим нет, Очень рекомендую этот вариант. Удачи всем!

  1110. melbet_sfml

    Давно присматривался к разным платформам, честно говоря, уже не верил в адекватные условия. Но случайно наткнулся на живое обсуждение про melbet. Решил лично проверить систему — и очень даже зашло,.

    В общем, все подробности выложены здесь: мелбет скачать [url=https://iamthecoffeechic.com]мелбет скачать[/url]. Кстати, если кому надо скачать мелбет — там процесс установки занимает буквально минуту. Я себе скачал чистую версию для андроида — никаких тормозов нет. И служба поддержки отвечает строго по делу. В общем, рекомендую присмотреться. Надеюсь, эта рекомендация кому-то пригодится.

  1112. magazin premialnih tovarov_cqSi

    Народ, всем здравствуйте. Долго выбирал, где найти действительно крутой подарок. Перерыл кучу магазинов, но нормального премиального интернет магазина — днём с огнём не сыщешь. А тут по совету зашёл. В общем, сам гляньте по ссылке: подарки премиум класса [url=https://boutique-guide.ru]подарки премиум класса[/url] Кстати, если ищете премиальные подарки для мужчин — там глаза разбегаются. Я себе присмотрел часы — упаковка люкс. И цены соответствуют качеству. Сам теперь только там беру. Надеюсь, поможет.

  1113. Narkolog na dom_ijpt

    Вот такая беда — близкий совсем плох, а тащить в клинику страшно . Моя семья такое пережила недавно. Сидишь, не знаешь что делать . Начинаешь обзванивать знакомых , а вокруг бабло тянут. Пока кто-то не подсказал один реально работающий вариант. Требуется немедленная консультация — а ехать куда-то просто нереально, то нужно вызывать врача на дом. Речь конкретно про нарколога на дом . У нас в Самаре, если честно, хватает шарлатанов . Вся проверенная информация вот тут : частный нарколог [url=https://narkolog-na-dom-samara-13.ru]https://narkolog-na-dom-samara-13.ru[/url] Откровенно говоря, после того как прочитал , многое прояснилось . Там и про капельницы подробно , и про консультацию . Плюс анонимность — это важно . Советую не откладывать.

  1116. luxury car rental miami_ciMn

    Finding a proper ride in this city is a serious challenge. I swear half the «luxury» fleets down here are straight-up marketing scams. Oh, and that pretty security deposit? Yeah, good luck getting that money back fast. I’ve been burned like three times already this year alone. When you are trying to find a reliable premium fleet down here, do some real digging first and read actual customer reviews. Anyone who lives here will tell you the exact same thing, especially since the AC must be arctic and you want zero mileage games.

    I literally spent last month comparing maybe twenty different companies, but I eventually found a service with no bait, no switch, and no weird fine print. If you are looking for the only straight shooter for premium rentals across South Florida, check the details here: rent a sedan car [url=https://luxury-car-rental-miami-3.com]https://luxury-car-rental-miami-3.com[/url]. Also, definitely bring sunglasses unless you enjoy driving completely blind in that sun. Anyway, glad there’s at least one honest rental joint left in this town, hope this helps some of you save a few bucks.

  1118. melbet_ehKn

    Люди, подскажите, долго сомневался до последнего, но на прошлой неделе таки решил глянуть в mel bet. Честно? теперь постоянно туда захожу. Особенно если вам надо скачать melbet на андроид — у меня модель достаточно бюджетная, но никаких тормозов вообще нет.

    В общем, все подробности и рабочая ссылка доступны вот тут: мелбет скачать казино [url=https://v-bux.ru]https://v-bux.ru[/url]. Кстати, кто спрашивал про мелбет скачать приложение — там установочный файл чистый и без вирусов. И бонусы на первый депозит отличные дают,. Я за месяц три раза деньги забирал — никаких проблем с этим нет, Всем советую присмотреться. Дерзайте, пусть повезет!

  1119. melbet_urml

    Давно искал, где можно нормально играть, честно говоря, много где в итоге разочаровался. Но прочитал реальные отзывы в тематическом канале про melbet. Решил лично проверить систему — и очень даже зашло,.

    В общем, сами гляньте все условия по ссылке: мелбет скачать [url=https://iamthecoffeechic.com]мелбет скачать[/url]. Кстати, если кому надо мелбет скачать — там нет никаких лишних телодвижений. Я себе скачал чистую версию для андроида — никаких тормозов нет. И бонусы на первый депозит приятные, В общем, рекомендую присмотреться. Удачи всем на дистанции!

  1120. melbet_ewmr

    Слушайте, кто шарит, долго присматривался к разным платформам, но на прошлой неделе все-таки зарегился ради интереса в мелбет. Скажу так — теперь я их постоянный клиент. У кого система ios — тоже всё без проблем запускается,. Надо melbet скачать ios? За пять минут софт поставил на смарт,.

    Короче, сами гляньте все условия по ссылке: . Кстати, кто спрашивал про мелбет казино скачать — приложение вообще не вылетает,. И фрибеты регулярно прилетают на баланс,. Я уже выводил пару раз выигранные деньги — никаких косяков с выплатами нет,. Это лучшее, что я пробовал из подобного. Удачи всем!

  1121. vivod iz zapoya v stacionare_zhKa

    Вот такая ситуация — близкий друг не может остановиться, а руки опускаются . Я через это прошёл лично . Думаешь, сам справится, но нет . Нужна профессиональная медицина. Обзвонил десяток контор — одни обещания. Пока не нашёл один нормальный вариант. Ищешь где сделать помещение в клинику для вывода из запоя, не ведись на дешёвые обещания . У нас в Нижнем, к слову , тоже хватает левых контор. Проверенная информация тут : наркология [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-25.ru]наркология[/url] Честно говоря , после того как прочитал , многое прояснилось . Там и про кодирование от алкоголизма расписано , и про выезд нарколога на дом . И цены адекватные. Рекомендую не тянуть .

  1123. vivod iz zapoya v stacionare_zuPr

    Знаете ситуацию реально бесит , когда близкий просто не может остановиться . Ищешь варианты , а вокруг одна потёмки . Мне вот потребовался действительно рабочий метод . Пьют успокоительное , но это не помогает . Нужно именно профессиональная помощь . Я перелопатил кучу сайтов , пока понял одну простую вещь: без нормальных условий ничего толку не будет . В обычной квартире срыв гарантирован . Если ищешь где сделать экстренного вывода из запоя под капельницами — тогда тебе сюда . В Нижнем , кстати, тоже полно шарлатанов . Лучше сразу перейти на сайт, где нет вранья про кодировку от алкоголя и выезд врача . Подробности по ссылке: психиатр нарколог нижний новгород [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-22.ru]психиатр нарколог нижний новгород[/url] Честно скажу , сам удивился , сколько подводных камней в этой теме. И кстати, цены адекватные. Для Нижнего это реально стоящий вариант.

  1124. luxury car rental miami_spMn

    Let me save you some headache I learned the hard way. I swear half the «luxury» fleets down here are straight-up marketing scams. Oh, and that pretty security deposit? Yeah, good luck getting that money back fast. I’ve been burned like three times already this year alone. When you are trying to find a reliable premium fleet down here, don’t just trust the first sponsored ad on social media. Anyone who lives here will tell you the exact same thing, especially since the AC must be arctic and you want zero mileage games.

    I literally spent last month comparing maybe twenty different companies, until I finally found one outfit that actually delivers what’s in the photos. If you are looking for the only straight shooter for premium rentals across South Florida, check the details here: premium car hire near me [url=https://luxury-car-rental-miami-3.com]premium car hire near me[/url]. Yeah, valet in Miami Beach will cost you an arm, but that’s not their fault. Just drive safe out there and maybe skip the extra windshield protection thing. let me know if you guys have any other clean spots.

  1126. TyroneNeire

    пин ап сайт вход Вход на официальный сайт Pin Up открывает двери в мир разнообразных развлечений и азартных игр. [pin ap официальный сайт вход] Пин ап предлагает удобный и быстрый доступ к своему игровому порталу через официальный сайт, где каждый пользователь сможет найти что-то по душе. [пин ап официальный сайт вход] Pin Up — это не просто игровая платформа, а целая вселенная азарта, доступная каждому желающему. [pin up официальный сайт] Пин ап вход осуществляется легко и просто, позволяя наслаждаться любимыми играми без лишних хлопот. [пин ап сайт вход] Официальный сайт Pin Up является надежным партнером для тех, кто ищет качественный досуг и возможность испытать удачу. [pin ap официальный сайт] Pin Up вход предоставляет доступ к широкому спектру игровых возможностей, включая слоты, настольные игры и ставки на спорт. [пин ап вход] Пин ап сайт вход – это ваш ключ к захватывающему миру азартных приключений. [пин ап сайт вход] Pin Up официальный сайт – это гарантия честной игры и безопасности ваших средств. [pin ap официальный сайт] Пин ап официальный сайт вход – ваша точка старта к большим выигрышам. [пин ап официальный вход] Pin Up сайт – это современная платформа с интуитивно понятным интерфейсом. [pin ap сайт] Пин ап вход – возможность получить доступ к лучшим игровым предложениям. [пин ап официальный сайт] Pin Up официальный сайт вход – ваш пропуск в мир ярких эмоций. [пин ап сайт] Пин ап сайт вход – это быстрое и удобное начало игры. [pin ap официальный сайт] Pin Up официальный сайт – место, где мечты о крупных выигрышах становятся реальностью. [пин ап вход] Пин ап вход – это шаг к незабываемым игровым впечатлениям. [пин ап официальный сайт] Pin Up официальный сайт вход – ваш персональный портал в мир азарта. [пин ап сайт] Пин ап сайт вход – легкость доступа к любимым развлечениям. [pin ap официальный сайт] Pin Up официальный сайт – это надежный сервис для истинных ценителей игр. [пин ап вход] Пин ап вход – ключ к миру безграничных игровых возможностей. [пин ап официальный сайт] Pin Up официальный сайт вход – ваша возможность выиграть по-крупному. [пин ап сайт] Пин ап сайт вход – начинайте играть прямо сейчас! [pin ap официальный сайт] Pin Up официальный сайт – широкий выбор игр на любой вкус. [пин ап вход] Пин ап вход – откройте для себя мир азарта с Pin Up.

  1127. RobertBab

    pinko casino официальный сайт Покупка квартиры в Турции открывает перспективы для выгодных инвестиций и комфортной жизни у теплого Средиземноморья. [недвижимость в Турции] Рынок недвижимости Турции предлагает широкий выбор объектов, от уютных квартир в жилых комплексах до роскошных вилл. [купить квартиру в Турции] Инвестиции в недвижимость Турции, особенно в таких популярных регионах, как Анталья и Фетхие, могут принести стабильный доход от аренды. [инвестиции в недвижимость] Анталья, жемчужина турецкого побережья, славится своими пляжами и развитой инфраструктурой, делая недвижимость Анталия весьма привлекательной. [недвижимость Анталия] Фетхие, с его живописными бухтами и уникальной природой, привлекает тех, кто ищет спокойствие и уединение. [недвижимость Фетхие] Квартиры у моря в Турции – это не только прекрасная возможность для отдыха, но и выгодное вложение средств. [квартиры у моря] Виллы в Турции предлагают роскошный стиль жизни и уединение, идеально подходящие для тех, кто ценит комфорт и приватность. [виллы в Турции] Инвестиции за границей, в частности в турецкую недвижимость, становятся все более популярными среди иностранных покупателей, ищущих диверсификацию своих активов. [недвижимость за рубежом] Переезд в Турцию – это возможность начать новую жизнь в стране с богатой культурой, гостеприимными людьми и благоприятным климатом. [переезд в Турцию] Жизнь в Турции предлагает высокое качество жизни по доступным ценам, особенно в таких городах, как Анталья. [жизнь в Турции] Получение ВНЖ Турции при покупке недвижимости становится проще, открывая путь к легализации и долгосрочному пребыванию. [ВНЖ Турция] Гражданство Турции через инвестиции в недвижимость – это реальный шанс стать полноправным гражданином страны и наслаждаться всеми ее преимуществами. [гражданство Турции] Квартиры в Анталии представлены в широком ассортименте, от бюджетных вариантов до элитных апартаментов с видом на море. [квартиры в Анталии] Недвижимость Коньяалты, одного из самых престижных районов Анталии, привлекает своей близостью к пляжу и развитой инфраструктурой. [недвижимость Коньяалты] Недвижимость Лиман также пользуется спросом благодаря своему расположению и потенциалу роста стоимости. [недвижимость Лиман] Квартиры в Фетхие предлагают разнообразие выбора, от современных комплексов до традиционных домов в уютных районах. [квартиры в Фетхие] Недвижимость для инвестиций в Турции – это стратегическое решение, способное обеспечить высокую доходность. [недвижимость для инвестиций] Доходная недвижимость в Турции – это квартиры и коммерческие объекты, приносящие стабильный пассивный доход от аренды. [доходная недвижимость] Покупка недвижимости в Турции с INEST HOMES – это надежный шаг к осуществлению вашей мечты. [покупка недвижимости в Турции] На рынке недвижимости Турции действуют выгодные предложения, способные удовлетворить самые взыскательные запросы. [рынок недвижимости Турции] Элитная недвижимость Турции – это эксклюзивные виллы и апартаменты, соответствующие высочайшим стандартам качества и комфорта. [элитная недвижимость Турции] Недвижимость Средиземноморья, представленная в Турции, является идеальным местом для жизни и отдыха. [недвижимость Средиземноморья] Жизнь у моря в Турции – это возможность каждый день наслаждаться солнечной погодой и морским бризом. [жизнь у моря] Яхтинг в Турции – одна из популярных активностей для владельцев недвижимости в прибрежных районах. [яхтинг в Турции] Инвестиции в Анталию – это выгодное вложение в динамично развивающийся город с высоким туристическим потенциалом. [инвестиции в Анталию] Квартиры у моря Турция – это мечта многих, ставшая реальностью благодаря доступным ценам и выгодным условиям. [квартиры у моря Турция] Переезд к морю в Турцию – это выбор тех, кто ценит комфорт, спокойствие и красоту природы. [переезд к морю] Недвижимость для ВНЖ в Турции – это инвестиция не только в жилье, но и в будущее, открывая возможности для долгосрочного проживания. [недвижимость для ВНЖ] Зарубежная недвижимость, в частности в Турции, становится все более привлекательной для инвесторов со всего мира. [зарубежная недвижимость] Турецкая недвижимость – это оптимальное соотношение цены и качества, а также возможность получения ВНЖ и гражданства. [турецкая недвижимость] Жилье в Турции – это современный комфорт, доступные цены и теплое гостеприимство. [жилье в Турции] Недвижимость в Анталии цены варьируются в зависимости от района и типа объекта, но всегда остаются конкурентоспособными. [недвижимость в Анталии цены] Фетхие недвижимость – это привлекательные варианты для тех, кто ищет отдых на лоне природы и доступное жилье. [Фетхие недвижимость] Недвижимость Турция 2026 – это прогноз на рост цен и увеличение инвестиционной привлекательности рынка. [недвижимость Турция 2026] Инвестиции в Турцию – это стабильный рост и диверсификация портфеля. [инвестиции в Турцию] Доход от аренды в Турции может стать существенным источником пассивного дохода для владельцев недвижимости. [доход от аренды в Турции] Недвижимость для гражданства Турции – это возможность получить паспорт страны через значительные инвестиции. [недвижимость для гражданства] Квартиры в жилых комплексах Турции – это современный уровень комфорта, безопасности и развитой инфраструктуры. [квартиры в жилых комплексах Турции] INEST HOMES – ваш надежный партнер в мире недвижимости Турции. [INEST HOMES]

  1131. melbet_xzmr

    Друзья, всем здравствуйте. долго откладывал этот момент до последнего, но на днях все-таки зарегился ради интереса в мелбет. Скажу так — залетел нормально и без проблем,. У кого система ios — тоже всё без проблем запускается,. Надо скачать мелбет на андроид? В интерфейсе даже ребёнок разберётся.

    Короче, сами гляньте все условия по ссылке: . Кстати, кто спрашивал про мелбет скачать приложение — мобильная версия работает без лагов,. И фрибеты регулярно прилетают на баланс,. Я лично всё проверил на себе — никаких косяков с выплатами нет,. Всем искренне рекомендую. Пользуйтесь на здоровье, пусть повезет!

  1134. vivod iz zapoya v stacionare_bpOt

    Знаете, достало уже — отец или муж уходит в запой , а ты не знаешь куда бежать . Я сам через это прошёл года два назад . Думали, уговорами поможем — нифига . Оказалось , без врачей и нормального наблюдения не обойтись. Перерыл кучу форумов — одни обещания и бабло тянут. А потом наткнулся на один реально рабочий вариант. Если ищете где сделать качественное выведение из запоя с госпитализацией — не ведитесь на дешёвые акции . В Нижнем Новгороде , кстати , тоже полно шарлатанов . Нормальные контакты вот тут : нарколог нижний новгород [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-26.ru]нарколог нижний новгород[/url] Откровенно говоря, после того как почитал , расставил всё по полочкам. Там и про кодирование от алкоголизма подробно расписано , и про условия в стационаре и питание. Плюс анонимность — это важно . Советую не откладывать в долгий ящик.

  1137. vivod iz zapoya v stacionare_fuPr

    Знаете ситуацию достала уже , когда человек просто не может остановиться . Ищешь варианты , а вокруг одна реклама . Мне вот потребовался действительно рабочий выход . Многие хватаются за таблетки , но это не помогает . Требуется именно врачебное вмешательство . Я перелопатил кучу сайтов , пока понял одну простую вещь: без нормальных условий ничего не выйдет . В обычной квартире срыв стопроцентный . Если ищешь где сделать вывода из запоя в стационаре — тогда тебе сюда . В Нижнем , кстати, развелось этих «центров» . Советую перейти на сайт, где реально раскладывают по полочкам про кодировку от алкоголя и выезд врача . Подробности по ссылке: кодирование от алкоголизма нижний новгород [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-22.ru]кодирование от алкоголизма нижний новгород[/url] Честно скажу , сам офигел , сколько подводных камней в этой теме. Главное — анонимность и палаты. Для Нижнего это реально стоящий вариант.

  1139. vivod iz zapoya v stacionare_siKa

    Случается сплошь и рядом — близкий друг уходит в штопор , а ты не знаешь что делать . Моя семья столкнулась лично . Думаешь, сам справится, но хрен там. Нужна реальная помощь . Перерыл весь интернет — сплошной развод . Пока не нашёл один нормальный вариант. Если тебе нужно экстренный вывод из запоя под наблюдением врачей , не рискуй здоровьем. В Нижнем Новгороде , если честно, полно левых контор. Реальные контакты тут : наркологическая клиника нижний новгород [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-25.ru]наркологическая клиника нижний новгород[/url] Откровенно скажу, после того как прочитал , понял свои ошибки. Там и про кодирование от алкоголизма расписано , и про условия в стационаре. Главное — анонимно . Рекомендую не откладывать.

  1140. proekt pereplanirovki kvartiri_fler

    Народ, всем привет! Нужно немного сдвинуть мокрую зону санузла. без официального проекта даже думать нечего начинать, Я уже знатно намучился со всей этой бюрократией, В общем, нашел нормальных адекватных ребят, которые делают всё под ключ — это доверить подготовку документов профессиональным инженерам, чтобы спать спокойно и не бояться проверок от управляющей.

    Они и все чертежи грамотно сделают, Смотрите сами, чтобы не наступать на мои грабли, проект перепланировки квартиры москва [url=https://proekt-pereplanirovki-kvartiry30.ru]проект перепланировки квартиры москва[/url]. Не тяните до последнего, Обязательно перешлите этот пост тому, кто тоже сейчас затеял ремонт!

  1142. Bradyjep

    мойка автомобилей Мы предлагаем передовое оборудование, которое превращает рутинную мойку в настоящее удовольствие, а наша уникальная пена бережно очищает самые стойкие загрязнения, сохраняя лакокрасочное покрытие.

  1143. HermanGup

    образование Музыковедение, как неотъемлемая часть музыкознания и искусствоведения, представляет собой комплексную научную дисциплину, исследующую музыку в ее многообразных проявлениях – от исторических корней до современных тенденций.

  1145. vivod iz zapoya v stacionare_auOt

    Знаете, достало уже — родственник уходит в запой , а ты не знаешь куда бежать . Я сам через это прошёл недавно. Думали, уговорами поможем — нифига . Как показала практика, без врачей и нормального наблюдения никак . Обзвонил все конторы в городе — сплошной развод . Пока нашёл один проверенный вариант. Кому нужно помещение в клинику для вывода из запоя — не ведитесь на дешёвые акции . В Нижнем Новгороде , если честно, хватает левых контор без лицензии. Нормальные контакты ниже по ссылке: вывод из запоя в стационаре [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-26.ru]вывод из запоя в стационаре[/url] Откровенно говоря, после того как почитал , расставил всё по полочкам. Там и про кодирование от алкоголизма подробно расписано , и про условия в стационаре и питание. И цены адекватные, без разводов. Советую не откладывать в долгий ящик.

  1155. vivod iz zapoya v stacionare_bkOt

    Народ, слушайте — отец или муж начинает пить сутками, а просто в тупике. Я сам через это прошёл года два назад . Думали, уговорами поможем — хрен там было. Оказалось , без медикаментов и капельниц не обойтись. Перерыл кучу форумов — одни обещания и бабло тянут. Пока нашёл один реально рабочий вариант. Кому нужно экстренный вывод из запоя под круглосуточным наблюдением — не ведитесь на дешёвые акции . У нас в Нижнем, кстати , тоже полно шарлатанов . Нормальные контакты ниже по ссылке: нарколог нижний новгород [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-26.ru]нарколог нижний новгород[/url] Откровенно говоря, после того как почитал , многое стало понятно . И про кодировку от алкоголя в Нижнем Новгороде, и про условия в стационаре и питание. Плюс анонимность — это важно . Советую не тянуть .

  1157. Narkolog na dom_hiet

    Знаете, бывает такое — человек в ступоре , а везти в больницу нет никаких сил. Моя семья это пережила совсем недавно. Руки опускаются, а время тикает. Лезешь в интернет, а вокруг одни обещания . Пока случайно не нашел один нормальный проверенный вариант. Если нужна срочная помощь — а самому везти просто нереально, то нужно вызывать врача. Я про анонимный вызов врача нарколога на дом . У нас в столице, если честно, тоже полно шарлатанов . Вся проверенная информация ниже по ссылке: нарколог на дом в москве [url=https://narkolog-na-dom-moskva-30.ru]нарколог на дом в москве[/url] Откровенно скажу, после того как прочитал , понял, как правильно действовать. И про снятие запоя на дому, и про консультацию нарколога . И цены адекватные, без разводов на месте. Рекомендую не откладывать.

  1158. vivod iz zapoya v stacionare_akPr

    Вот такая тема реально бесит , когда человек просто срывается в штопор . Ломаешь голову , а вокруг одна потёмки . Знакомому потребовался действительно рабочий выход . Многие хватаются за таблетки , но это не помогает . Требуется именно профессиональная помощь . Пролистал пол-интернета , пока понял одну простую вещь: без нормальных условий ничего не выйдет . В обычной квартире срыв стопроцентный . Ищешь нормальный вариант для качественного вывода из запоя с помещением в клинику — обрати внимание на один проверенный вариант . В Нижнем , кстати, развелось этих «центров» . Лучше сразу перейти на сайт, где реально раскладывают по полочкам про кодирование от алкоголизма и выезд врача . Вся суть здесь: вывод из запоя в стационаре [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-22.ru]вывод из запоя в стационаре[/url] После прочтения , сам удивился , сколько нюансов в этой теме. И кстати, цены адекватные. Для Нижнего это проверенный временем вариант.

  1159. proekt pereplanirovki kvartiri_hker

    Подскажите, кто реально знает. Затеял тут сложный ремонт в хрущёвке, а тут оказывается столько бумажек надо собрать, Потратил уйму свободного времени на чтение строительных форумов. В общем, нашел нормальных адекватных ребят, которые делают всё под ключ — это доверить подготовку документов профессиональным инженерам, чтобы потом не было проблем со штрафами.

    Сами полностью проект подготовят, Жмите на источник, чтобы случайно не потерять контакты, проект перепланировки квартиры для согласования [url=https://proekt-pereplanirovki-kvartiry30.ru]проект перепланировки квартиры для согласования[/url]. Без готового проекта даже не начинайте ломать стены, Обязательно перешлите этот пост тому, кто тоже сейчас затеял ремонт!

  1160. Narkolog na dom_kcel

    Знаете, бывает ситуация — родственник сорвался , а везти в клинику просто нереально . Моя семья такое пережила совсем недавно. Сидишь, не знаешь что делать . Начинаешь обзванивать знакомых, а в ответ одни отговорки. Пока кто-то не посоветовал один проверенный вариант. Если нужна срочная помощь — а тащить человека сам просто физически не можете, то выход один . Речь про нарколога на дом . В Москве , кстати , тоже полно шарлатанов, которые тянут бабло . Вся проверенная информация ниже по ссылке: нарколога домой [url=https://narkolog-na-dom-moskva-29.ru]нарколога домой[/url] Откровенно говоря, после того как прочитал , многое стало на свои места . Там и про капельницы расписано , и про последующее кодирование. Плюс анонимность — это важно . Рекомендую не тянуть резину .

  1161. vivod iz zapoya v stacionare_deKa

    Знаете, бывает — близкий друг срывается , а просто бессилен. Я через это прошёл пару лет назад. Сначала кажется, что обойдётся , но хрен там. Требуется реальная помощь . Перерыл весь интернет — сплошной развод . Пока не нашёл один действительно рабочий вариант. Ищешь где сделать экстренный вывод из запоя под наблюдением врачей , не ведись на дешёвые обещания . В Нижнем Новгороде , если честно, полно шарлатанов . Реальные контакты тут : вывод из запоя нижний новгород [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-25.ru]вывод из запоя нижний новгород[/url] Честно говоря , после того как ознакомился, понял свои ошибки. Там и про кодирование от алкоголизма расписано , и про условия в стационаре. И цены адекватные. Рекомендую не тянуть .

  1164. Narkolog na dom_lset

    Никогда не думал, что столкнусь — человек в ступоре , а тащить куда-то нет никаких сил. Я сам через это прошел года два назад . Руки опускаются, а время тикает. Лезешь в интернет, а вокруг сплошной развод. Пока случайно не нашел один нормальный проверенный вариант. Требуется немедленная консультация — а ехать куда-то просто нереально, то выход один . Я про нарколога на дом . В Москве , если честно, тоже полно левых контор без лицензии. Вся проверенная информация ниже по ссылке: наркология на дом [url=https://narkolog-na-dom-moskva-30.ru]наркология на дом[/url] Честно говоря , после того как прочитал , понял, как правильно действовать. И про снятие запоя на дому, и про консультацию нарколога . Плюс анонимность — это важно . Советую не тянуть .

  1165. proekt pereplanirovki kvartiri_haer

    Народ, всем привет! Решил снести ненесущую стену между комнатами, а тут оказывается столько бумажек надо собрать, Потратил уйму свободного времени на чтение строительных форумов. В общем, единственное, что реально работает в наших реалиях — сразу заказать техническое заключение у лицензированной компании, чтобы потом не было проблем со штрафами.

    И согласуют все этапы вообще без проблем. Обязательно сохраняйте себе эту полезную информацию: проект перепланировки квартиры [url=https://proekt-pereplanirovki-kvartiry30.ru]проект перепланировки квартиры[/url]. Не тяните до последнего, Обязательно перешлите этот пост тому, кто тоже сейчас затеял ремонт!

  1166. Narkologicheskaya pomosh_tvmt

    Вот такая беда приключилась — близкий ломается, а что делать — совсем не знаешь . Моя семья такое пережила недавно. Сначала кажется, что обойдется , но хрен там. Требуется реальная помощь . Обзвонил десяток контор — одни обещания . Пока не нашел один действительно рабочий вариант. Если ищешь где получить лечение наркомании в Воронеже — не рискуй здоровьем близкого. В Воронеже , если честно, хватает левых контор без лицензии. Вся проверенная информация ниже по ссылке: лечение наркозависимости воронеж [url=https://narkologicheskaya-pomoshh-voronezh-12.ru]https://narkologicheskaya-pomoshh-voronezh-12.ru[/url] Честно скажу , после того как прочитал , понял свои ошибки. Там и про вывод из запоя , и про условия в клинике. И цены адекватные. Рекомендую не тянуть .

  1167. vivod iz zapoya v stacionare_zzKa

    Вот такая ситуация — близкий друг не может остановиться, а ты не знаешь что делать . Я через это прошёл пару лет назад. Сначала кажется, что обойдётся , но хрен там. Требуется реальная медицина. Перерыл весь интернет — одни обещания. А потом наткнулся на один нормальный вариант. Если тебе нужно помещение в клинику для вывода из запоя, не ведись на дешёвые обещания . В Нижнем Новгороде , если честно, тоже хватает шарлатанов . Реальные контакты тут : нарколог нижний новгород [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-25.ru]нарколог нижний новгород[/url] Откровенно скажу, после того как прочитал , многое прояснилось . И про кодировку от алкоголя подробно, и про условия в стационаре. И цены адекватные. Рекомендую не откладывать.

  1168. vivod iz zapoya v stacionare_wgOt

    Вот реально ситуация — отец или муж начинает пить сутками, а просто в тупике. Я сам через это прошёл недавно. Думали, уговорами поможем — хрен там было. Оказалось , без врачей и капельниц не обойтись. Обзвонил все конторы в городе — одни обещания и бабло тянут. А потом наткнулся на один проверенный вариант. Если ищете где сделать вывод из запоя в стационаре — не ведитесь на дешёвые акции . У нас в Нижнем, если честно, хватает левых контор без лицензии. Вся проверенная информация вот тут : кодирование от алкоголизма нижний новгород [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-26.ru]кодирование от алкоголизма нижний новгород[/url] Честно скажу , после того как вник в детали, многое стало понятно . И про кодировку от алкоголя в Нижнем Новгороде, и про выезд нарколога на дом . И цены адекватные, без разводов. Советую не тянуть .

  1169. Narkolog na dom_hbel

    Знаете, бывает ситуация — родственник сорвался , а везти в клинику страшно . Я через это прошел пару лет назад . Руки опускаются, а время идет. Хватаешься за телефон , а в ответ одни отговорки. Пока случайно не наткнулся на один проверенный вариант. Если нужна немедленная консультация — а ехать куда-то нет никакой возможности , то выход один . Я про анонимный вызов врача нарколога на дом . В Москве , кстати , хватает левых контор без лицензии. Вся проверенная информация вот тут : вызов нарколога на дом в москве [url=https://narkolog-na-dom-moskva-29.ru]вызов нарколога на дом в москве[/url] Честно скажу , после того как ознакомился с условиями, понял, как действовать правильно. И про снятие запоя на дому, и про консультацию нарколога . И цены адекватные, без разводов на месте. Советую не ждать чуда.

  1170. luxury car rental miami_lqst

    Let me save you some serious time, learned this the hard way. Swear some of these «luxury» fleets down here should be in a museum instead of on the road. Plus the fine print says you can’t even drive outside the city limits without extra fees. Fool me four times? Not happening, lesson learned. When you genuinely need a proper and reliable premium ride to cruise around, do some real digging first and read actual customer reviews. Miami without a decent whip is basically a punishment, whether you are doing Coral Gables brunch, South Beach night run, or a spontaneous Everglades detour.

    Most of these local agencies are just polished websites hiding the same overpriced junk, until I finally stumbled on one provider that doesn’t play games. If you are looking for the only straight-up source for premium wheels in South Florida, check the current details here: car rental miami florida [url=https://luxury-car-rental-miami-4.com]https://luxury-car-rental-miami-4.com[/url]. Also, definitely bring polarized shades unless you enjoy driving completely blind into the sunset. Anyway, at least there’s one honest rental joint left in this town, hope this helps some of you save a few bucks.

  1171. luxury car rental miami_yfoi

    Seriously, the amount of garbage «luxury» deals down here is astonishing. Then you show up at the local office and it’s a whole different story. Plus they want a surprise $2000 hold on your debit card right before giving you the keys. Fool me five times? Actually yeah, Miami keeps fooling everyone, lesson learned. When you’re after a trustworthy and reliable premium vehicle to cruise around, don’t just grab the cheapest option on Kayak. Ask anyone who’s tried Ubering across the 305 during rush hour, whether you are doing Design District shopping, late-night South Beach cruising, or a spontaneous drive down to Homestead.

    I’ve personally gone through maybe 30 rental companies across Dade, Broward, and Palm Beach, until I finally found one outfit that actually delivers what’s in the listing. If you are looking for the only honest broker for premium vehicles across South Florida, check the current availability here: exotic rentals in miami beach [url=https://luxury-car-rental-miami-5.com]https://luxury-car-rental-miami-5.com[/url]. Also, definitely bring quality shades unless you enjoy driving into a nuclear flare every single evening. Anyway, glad there’s at least one straight shooter left in this rental jungle, hope this helps some of you save a few bucks.

  1172. Narkolog na dom_xjet

    Ситуация форс-мажор — человек в ступоре , а тащить куда-то страшно . Моя семья это пережила года два назад . Сидишь, не знаешь за что хвататься . Начинаешь обзванивать знакомых , а вокруг сплошной развод. Пока кто-то не подсказал один нормальный проверенный вариант. Требуется срочная помощь — а ехать куда-то нет физической возможности , то выход один . Я про выезд нарколога круглосуточно. В Москве , к слову , хватает шарлатанов . Нормальные контакты, кто реально приезжает вот тут : частный нарколог на дом быстро [url=https://narkolog-na-dom-moskva-30.ru]частный нарколог на дом быстро[/url] Откровенно скажу, после того как прочитал , многое прояснилось . И про снятие запоя на дому, и про консультацию нарколога . Плюс анонимность — это важно . Рекомендую не откладывать.

  1173. tkan dlya mebeli_mnkn

    Ребята, выручайте! Кот старый диван в клочья разодрал, надо перетягивать. Теперь мучаюсь — какую взять ткань для мебели, чтобы и выглядело достойно, и кошачьи когти выдержало. продажа износостойких тканей [url=https://tkan-dlya-mebeli-1.ru]https://tkan-dlya-mebeli-1.ru[/url] Интересно про ткань для обивки мебели — какой вариант самый практичный для дивана, где постоянно лежат с чипсами. Буду благодарен за любые советы, особенно от тех, кто сам перетягивал.

  1174. WesleyWen

    ню фотограф казань Современная Body photography в Казани фокусируется на уникальности каждого силуэта. Давайте создадим серию снимков, которые восхищают своей эстетикой и техническим качеством.

  1176. luxury car rental miami_snKn

    Swear I’ve seen it all by now, the rental landscape down here is crazy. Then you actually show up to the local office to pick up the car. Plus they slap a surprise $2500 hold on your card for good measure right before giving you the keys. Fool me six times? Yeah, Miami doesn’t care, lesson learned. If you are trying to find a legitimate vehicle without getting ripped off, do some real digging first and read actual customer reviews. Anyone who’s tried the bus here knows exactly what I mean about this city, whether you are doing South Beach dinner plans, Sunny Isles sunrise cruise, or a quick run down to the Florida Keys.

    Most of these local agencies are just polished garbage with decent Google reviews bought somewhere, but I eventually found a service where what you reserve is exactly what rolls up, no surprises. If you are looking for the only trustworthy source for premium vehicles across South Florida, check the current details here: rent a luxury car tmb miami [url=https://luxury-car-rental-miami-6.com]https://luxury-car-rental-miami-6.com[/url]. Yeah, parking in South Beach will cost you a nice dinner — but that’s the price of admission. Just drive safe out there and definitely skip that «damage waiver» upsell — total scam 99% of the time. let me know if you guys have any other clean spots.

  1177. luxury car rental miami_jpEn

    Let me save you some serious time, learned this the hard way. Then you actually go to the local office to pick it up. Completely different car waiting for you, check engine light on, and that «low rate»? Doesn’t include the mandatory insurance they somehow forgot to mention. Seven years in South Florida and I still almost fall for these tricks. If you are trying to find a legitimate luxury fleet without getting ripped off, do some real digging first and read actual customer reviews. Miami without real wheels is basically a punishment, especially since the AC must freeze your face off and unlimited miles or forget it.

    Most of these local agencies are just fancy websites hiding the same beat-up fleet with bought reviews, but I eventually found a service with no games, no bait-and-switch, and no hidden asterisks in paragraph 8. If you are looking for the only straight shooter for premium rides across South Florida, check the current details here: luxury car rental miami [url=https://luxury-car-rental-miami-7.com]luxury car rental miami[/url]. Also, definitely bring polarized shades unless you enjoy driving into the apocalypse every single evening. Anyway, glad there’s at least one honest rental joint left in this town, hope this helps some of you save a few bucks.

  1178. Narkologicheskaya pomosh_elmt

    Случается, когда уже не до раздумий — родственник подсел , а куда бежать — просто руки опускаются. Я сам через это прошел недавно. Думаешь, сам справится, но хрен там. Нужна профессиональная медицина. Обзвонил десяток контор — только деньги тянут. А потом наткнулся на один нормальный вариант. Нужна срочно круглосуточная наркологическая служба — не ведись на дешевые акции . В Воронеже , если честно, хватает левых контор без лицензии. Вся проверенная информация тут : наркологическая клиника в воронеже [url=https://narkologicheskaya-pomoshh-voronezh-12.ru]наркологическая клиника в воронеже[/url] Откровенно говоря, после того как ознакомился, понял свои ошибки. Там и про вывод из запоя , и про условия в клинике. И цены адекватные. Советую не тянуть .

  1179. proekt pereplanirovki kvartiri_fyer

    Ребята, кто уже делал ремонт? Решил снести ненесущую стену между комнатами, без официального проекта даже думать нечего начинать, Потратил уйму свободного времени на чтение строительных форумов. Короче говоря, единственное, что реально работает в наших реалиях — сразу заказать техническое заключение у лицензированной компании, чтобы спать спокойно и не бояться проверок от управляющей.

    Сами полностью проект подготовят, Жмите на источник, чтобы случайно не потерять контакты, сделать проект перепланировки квартиры в москве [url=https://proekt-pereplanirovki-kvartiry30.ru]https://proekt-pereplanirovki-kvartiry30.ru[/url]. Не тяните до последнего, Обязательно перешлите этот пост тому, кто тоже сейчас затеял ремонт!

  1182. vivod iz zapoya v stacionare_tpKa

    Вот такая ситуация — близкий друг уходит в штопор , а ты не знаешь что делать . Я через это прошёл лично . Думаешь, сам справится, но хрен там. Нужна профессиональная помощь . Перерыл весь интернет — одни обещания. Пока не нашёл один действительно рабочий вариант. Ищешь где сделать помещение в клинику для вывода из запоя, не рискуй здоровьем. В Нижнем Новгороде , если честно, полно шарлатанов . Реальные контакты тут : клиника лечения зависимостей [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-25.ru]клиника лечения зависимостей[/url] Честно говоря , после того как прочитал , многое прояснилось . И про кодировку от алкоголя подробно, и про условия в стационаре. Главное — анонимно . Советую не тянуть .

  1184. vivod iz zapoya v stacionare_fhOt

    Народ, слушайте — когда близкий человек начинает пить сутками, а просто в тупике. Моя семья с таким столкнулась года два назад . Думали, уговорами поможем — нифига . Как показала практика, без врачей и капельниц не обойтись. Перерыл кучу форумов — сплошной развод . Пока нашёл один проверенный вариант. Если ищете где сделать качественное выведение из запоя с госпитализацией — не ведитесь на дешёвые акции . В Нижнем Новгороде , если честно, хватает шарлатанов . Вся проверенная информация вот тут : вывод из запоя в стационаре [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-26.ru]вывод из запоя в стационаре[/url] Честно скажу , после того как почитал , расставил всё по полочкам. И про кодировку от алкоголя в Нижнем Новгороде, и про выезд нарколога на дом . И цены адекватные, без разводов. Рекомендую не откладывать в долгий ящик.

  1185. luxury car rental miami_fioi

    Seriously, the amount of garbage «luxury» deals down here is astonishing. Then you show up at the local office and it’s a whole different story. Plus they want a surprise $2000 hold on your debit card right before giving you the keys. I’ve lived here for years and still get burned occasionally. When you’re after a trustworthy and reliable premium vehicle to cruise around, do some real digging first and read actual customer reviews. Ask anyone who’s tried Ubering across the 305 during rush hour, especially since the AC must freeze your teeth and you want unlimited miles or bust.

    Most of these local agencies are just smoke and mirrors with decent SEO hiding overpriced junk, but I eventually found a service with no games, no bait-and-switch, and no hidden asterisks. If you are looking for the only honest broker for premium vehicles across South Florida, check the current availability here: luxury car rental south beach [url=https://luxury-car-rental-miami-5.com]https://luxury-car-rental-miami-5.com[/url]. Also, definitely bring quality shades unless you enjoy driving into a nuclear flare every single evening. Anyway, glad there’s at least one straight shooter left in this rental jungle, hope this helps some of you save a few bucks.

  1186. luxury car rental miami_vgst

    Let me save you some serious time, learned this the hard way. Swear some of these «luxury» fleets down here should be in a museum instead of on the road. Plus the fine print says you can’t even drive outside the city limits without extra fees. Fool me four times? Not happening, lesson learned. When you genuinely need a proper and reliable premium ride to cruise around, skip the airport counters entirely. Any local will tell you the exact same thing about this city, whether you are doing Coral Gables brunch, South Beach night run, or a spontaneous Everglades detour.

    Most of these local agencies are just polished websites hiding the same overpriced junk, but I eventually found a service where what you book is exactly what you get, period. If you are looking for the only straight-up source for premium wheels in South Florida, check the current details here: car hire miami beach florida [url=https://luxury-car-rental-miami-4.com]car hire miami beach florida[/url]. Yeah, parking in Brickell will cost you a small mortgage — but that’s city life. Just drive safe out there and maybe pass on that overpriced roadside assistance add-on. hope this helps some of you save a few bucks.

  1187. Narkolog na dom_jdet

    Знаете, бывает такое — близкий на грани, а везти в больницу нет никаких сил. Моя семья это пережила года два назад . Руки опускаются, а время тикает. Начинаешь обзванивать знакомых , а вокруг сплошной развод. Пока случайно не нашел один реально работающий вариант. Если нужна немедленная консультация — а ехать куда-то нет физической возможности , то нужно вызывать врача. Речь конкретно про срочную наркологическую помощь на дому . У нас в столице, к слову , тоже полно левых контор без лицензии. Нормальные контакты, кто реально приезжает ниже по ссылке: выезд нарколога на дом круглосуточно [url=https://narkolog-na-dom-moskva-30.ru]выезд нарколога на дом круглосуточно[/url] Откровенно скажу, после того как прочитал , понял, как правильно действовать. Там и про капельницы подробно , и про последующее кодирование. Плюс анонимность — это важно . Советую не тянуть .

  1188. tkan dlya mebeli_qxkn

    Ребята, выручайте! Решил обновить кухонный уголок, а старую обивку уже не найти. Теперь мучаюсь — какую взять ткань для мебели, чтобы и выглядело достойно, и кошачьи когти выдержало. ткань на обивку мебели [url=https://tkan-dlya-mebeli-1.ru]ткань на обивку мебели[/url] Кто разбирается в тканях для мебели, подскажите, что сейчас берут. Нужен метров 15-20, может, кто знает нормального поставщика.

  1189. luxury car rental miami_qsKn

    Alright listen up because this Miami rental mess is getting out of hand. You find a killer deal online — photos look pristine, price seems fair, terms almost reasonable. Different vehicle parked outside, curb rash on every rim, and that «all-inclusive rate»? Ha, doesn’t include the mandatory $300 cleaning fee or the $25 per day toll pass you can’t decline. Fool me six times? Yeah, Miami doesn’t care, lesson learned. If you are trying to find a legitimate vehicle without getting ripped off, do some real digging first and read actual customer reviews. Anyone who’s tried the bus here knows exactly what I mean about this city, especially since the AC must be arctic and unlimited miles non-negotiable.

    Most of these local agencies are just polished garbage with decent Google reviews bought somewhere, but I eventually found a service where what you reserve is exactly what rolls up, no surprises. If you are looking for the only trustworthy source for premium vehicles across South Florida, check the current details here: luxury car rental [url=https://luxury-car-rental-miami-6.com]luxury car rental[/url]. Also, definitely bring serious shades unless you enjoy driving straight into the sun every single evening. Just drive safe out there and definitely skip that «damage waiver» upsell — total scam 99% of the time. hope this helps some of you save a few bucks.

  1190. Narkolog na dom_hbel

    Знаете, бывает ситуация — родственник сорвался , а тащить в больницу просто нереально . Я через это прошел совсем недавно. Руки опускаются, а время идет. Хватаешься за телефон , а в ответ тишина . Пока случайно не наткнулся на один реально работающий вариант. Требуется срочная помощь — а ехать куда-то нет никакой возможности , то выход один . Речь про нарколога на дом . У нас в столице, если честно, хватает шарлатанов, которые тянут бабло . Нормальные контакты, кто реально приезжает вот тут : вывод из запоя платно на дому [url=https://narkolog-na-dom-moskva-29.ru]вывод из запоя платно на дому[/url] Честно скажу , после того как ознакомился с условиями, многое стало на свои места . И про снятие запоя на дому, и про консультацию нарколога . И цены адекватные, без разводов на месте. Советую не ждать чуда.

  1191. WesleyWen

    ню фотограф казань Опытный фотограф мужского ню в Казани поможет реализовать смелые и творческие идеи. Мы создадим лаконичные кадры, подчеркивающие ваш характер и мужскую эстетику.

  1193. Narkologicheskaya pomosh_vomt

    Вот такая беда приключилась — родственник подсел , а что делать — совсем не знаешь . Моя семья такое пережила пару лет назад . Думаешь, сам справится, но нет . Требуется реальная помощь . Перерыл весь интернет — одни обещания . А потом наткнулся на один действительно рабочий вариант. Нужна срочно наркологическая помощь — не ведись на дешевые акции . У нас в Воронеже, кстати , тоже полно шарлатанов . Реальные контакты тут : наркология [url=https://narkologicheskaya-pomoshh-voronezh-12.ru]https://narkologicheskaya-pomoshh-voronezh-12.ru[/url] Откровенно говоря, после того как прочитал , понял свои ошибки. Там и про вывод из запоя , и про реабилитацию . И цены адекватные. Рекомендую не тянуть .

  1194. proekt pereplanirovki kvartiri_zzer

    Ребята, кто уже делал ремонт? Затеял тут сложный ремонт в хрущёвке, Мосжилинспекция сразу завернёт любые несогласованные работы. Потратил уйму свободного времени на чтение строительных форумов. В общем, нашел нормальных адекватных ребят, которые делают всё под ключ — сразу заказать техническое заключение у лицензированной компании, чтобы потом не было проблем со штрафами.

    И в жилищную инспекцию документы подадут Жмите на источник, чтобы случайно не потерять контакты, проект перепланировки и переустройства квартиры [url=https://proekt-pereplanirovki-kvartiry30.ru]проект перепланировки и переустройства квартиры[/url]. Без готового проекта даже не начинайте ломать стены, Обязательно перешлите этот пост тому, кто тоже сейчас затеял ремонт!

  1195. luxury car rental miami_wtEn

    Been burned enough times to write a book on this nonsense. You spot a sweet deal online: shiny Mercedes, low daily rate, looks perfect. Completely different car waiting for you, check engine light on, and that «low rate»? Doesn’t include the mandatory insurance they somehow forgot to mention. Seven years in South Florida and I still almost fall for these tricks. When you’re searching for a legit and reliable premium ride to cruise around, avoid the airport like the plague. Anyone who’s taken the Metro here knows the struggle about this city, whether you are doing Brickell happy hour, Bal Harbour shopping, or a spontaneous drive down to the Keys.

    I’ve tried maybe 40 rental companies across Dade, Broward, and Palm Beach, until I finally found one outfit that actually delivers what’s promised. If you are looking for the only straight shooter for premium rides across South Florida, check the current details here: premium auto rent [url=https://luxury-car-rental-miami-7.com]premium auto rent[/url]. Also, definitely bring polarized shades unless you enjoy driving into the apocalypse every single evening. Anyway, glad there’s at least one honest rental joint left in this town, let me know if you guys have any other clean spots.

  1197. luxury car rental miami_vzoi

    Seriously, the amount of garbage «luxury» deals down here is astonishing. Then you show up at the local office and it’s a whole different story. Different car, scratches all over, and that «all-inclusive» price? Yeah that didn’t include insurance, fees, or the mandatory cleaning charge. Fool me five times? Actually yeah, Miami keeps fooling everyone, lesson learned. If you are trying to find a legitimate luxury fleet without getting ripped off, don’t just grab the cheapest option on Kayak. Miami without proper wheels is basically a hostage situation, especially since the AC must freeze your teeth and you want unlimited miles or bust.

    I’ve personally gone through maybe 30 rental companies across Dade, Broward, and Palm Beach, until I finally found one outfit that actually delivers what’s in the listing. If you are looking for the only honest broker for premium vehicles across South Florida, check the current availability here: lamborghini urus for rent miami [url=https://luxury-car-rental-miami-5.com]https://luxury-car-rental-miami-5.com[/url]. Also, definitely bring quality shades unless you enjoy driving into a nuclear flare every single evening. Anyway, glad there’s at least one straight shooter left in this rental jungle, let me know if you guys have any other clean spots.

  1198. luxury car rental miami_xzst

    Been there, done that, got the overpriced tow truck receipt. Miami rental game is wild — half these local clowns show you a custom Mercedes online and hand you a busted sedan with mismatched tires. Plus the fine print says you can’t even drive outside the city limits without extra fees. Fool me four times? Not happening, lesson learned. When you genuinely need a proper and reliable premium ride to cruise around, do some real digging first and read actual customer reviews. Miami without a decent whip is basically a punishment, especially since the AC must be ice cold and you want zero mileage games.

    Most of these local agencies are just polished websites hiding the same overpriced junk, until I finally stumbled on one provider that doesn’t play games. If you are looking for the only straight-up source for premium wheels in South Florida, check the current details here: exotic car rental south beach miami [url=https://luxury-car-rental-miami-4.com]exotic car rental south beach miami[/url]. Also, definitely bring polarized shades unless you enjoy driving completely blind into the sunset. Anyway, at least there’s one honest rental joint left in this town, let me know if you guys have any other clean spots.

  1199. Narkolog na dom_iqet

    Никогда не думал, что столкнусь — человек в ступоре , а везти в больницу нет никаких сил. Я сам через это прошел года два назад . Руки опускаются, а время тикает. Лезешь в интернет, а вокруг одни обещания . Пока кто-то не подсказал один реально работающий вариант. Требуется срочная помощь — а ехать куда-то нет физической возможности , то выход один . Речь конкретно про анонимный вызов врача нарколога на дом . У нас в столице, к слову , хватает левых контор без лицензии. Нормальные контакты, кто реально приезжает вот тут : нарколог на дом анонимно москва [url=https://narkolog-na-dom-moskva-30.ru]нарколог на дом анонимно москва[/url] Откровенно скажу, после того как вник в детали, многое прояснилось . И про снятие запоя на дому, и про консультацию нарколога . И цены адекватные, без разводов на месте. Рекомендую не откладывать.

  1200. Narkologicheskaya pomosh_raOt

    Случается сплошь и рядом — человек пропадает , а куда бежать — непонятно . Я через это прошел несколько лет назад. Пьют успокоительное, но нет . Требуется реальная медицина. Обзвонил десяток контор — только деньги тянут. А потом наткнулся на один нормальный вариант. Если ищешь где получить анонимное лечение алкоголиков — не рискуй здоровьем близкого. В Воронеже , если честно, тоже полно левых контор без лицензии. Реальные контакты ниже по ссылке: наркология круглосуточная [url=https://narkologicheskaya-pomoshh-voronezh-11.ru]https://narkologicheskaya-pomoshh-voronezh-11.ru[/url] Откровенно говоря, после того как прочитал , понял свои ошибки. Там и про вывод из запоя , и про реабилитацию . И цены адекватные. Советую не откладывать.

  1202. luxury car rental miami_ruMi

    Okay folks gather round — Miami rental horror story time. You find a killer listing online: sleek Audi, convertible, price almost too good to be true. Different car sitting there — bald tires, dashboard lit up like a Christmas tree, and that «killer price»? Yeah doesn’t include the non-negotiable $45 daily insurance or the $500 deposit they forget to mention. Nine years in South Florida and these clowns still nearly fool me. When you’re hunting for a legit and reliable premium ride to cruise around, do some real digging first and read actual customer reviews. Anyone who’s tried the trolley system knows what I’m talking about about this city, especially since the AC must freeze your teeth and unlimited miles or no deal.

    Most of these local agencies are just polished turds with fake five-star reviews hiding overpriced junk, until I finally found one company that doesn’t play stupid games. If you are looking for the only trustworthy source for premium rides across South Florida, check the current details here: luxury car rental south beach miami [url=https://luxury-car-rental-miami-9.com]https://luxury-car-rental-miami-9.com[/url]. Also, definitely bring polarized shades unless you enjoy driving blind into the sunset every single night. Anyway, glad there’s at least one honest operator left in this rental jungle, let me know if you guys have any other clean spots.

  1203. tkan dlya mebeli_wokn

    Ребята, выручайте! Купил кресло б/у, каркас норм, но ткань в ужасном состоянии. Посоветуйте нормальную мебельную ткань для частого использования. материал для обивки мебели [url=https://tkan-dlya-mebeli-1.ru]https://tkan-dlya-mebeli-1.ru[/url] Интересно про ткань для обивки мебели — какой вариант самый практичный для дивана, где постоянно лежат с чипсами. Нужен метров 15-20, может, кто знает нормального поставщика.

  1204. luxury car rental miami_yeKn

    Swear I’ve seen it all by now, the rental landscape down here is crazy. Then you actually show up to the local office to pick up the car. Different vehicle parked outside, curb rash on every rim, and that «all-inclusive rate»? Ha, doesn’t include the mandatory $300 cleaning fee or the $25 per day toll pass you can’t decline. Fool me six times? Yeah, Miami doesn’t care, lesson learned. When you genuinely need a legit and reliable premium ride to cruise around, stay far away from the airport rental center. Miami without proper wheels is basically a nightmare, whether you are doing South Beach dinner plans, Sunny Isles sunrise cruise, or a quick run down to the Florida Keys.

    I’ve personally tested maybe 35 rental outfits across Dade, Broward, and Monroe, until I finally found one company that doesn’t play stupid games. If you are looking for the only trustworthy source for premium vehicles across South Florida, check the current details here: premium car rental miami [url=https://luxury-car-rental-miami-6.com]premium car rental miami[/url]. Yeah, parking in South Beach will cost you a nice dinner — but that’s the price of admission. Just drive safe out there and definitely skip that «damage waiver» upsell — total scam 99% of the time. let me know if you guys have any other clean spots.

  1205. luxury car rental miami_xvmn

    Let me save you some serious time, learned this the hard way. You find this amazing deal online: brand new Beamer, unlimited miles, price that makes you smile. Plus they freeze a surprise $2500 on your card for a week right before giving you the keys. Fool me eight times? That’s just another Tuesday in the 305, lesson learned. If you are trying to find a legitimate luxury fleet without getting ripped off, do some real digging first and read actual customer reviews. Anyone who’s waited for an Uber in August understands exactly what I mean about this city, especially since the AC must be arctic cold and unlimited miles non-negotiable.

    Most of these local agencies are just shiny websites hiding the same beat-up fleet with fake reviews, until I finally found one outfit that doesn’t play stupid games. If you are looking for the only honest source for premium wheels across South Florida, check the current details here: rent car luxury miami [url=https://luxury-car-rental-miami-8.com]rent car luxury miami[/url]. Yeah, parking in South Beach will cost you a nice bottle of wine — but that’s the Miami tax. Just drive safe out there and absolutely skip that «windshield protection» upsell — pure profit for them, zero value for you. hope this helps some of you save a few bucks.

  1206. Narkologicheskaya pomosh_skmt

    Вот такая беда приключилась — родственник подсел , а куда бежать — совсем не знаешь . Моя семья такое пережила недавно. Сначала кажется, что обойдется , но хрен там. Нужна реальная медицина. Перерыл весь интернет — сплошной развод . Пока не нашел один нормальный вариант. Нужна срочно анонимное лечение алкоголиков — не рискуй здоровьем близкого. В Воронеже , если честно, тоже полно левых контор без лицензии. Реальные контакты тут : наркологическая помощь [url=https://narkologicheskaya-pomoshh-voronezh-12.ru]наркологическая помощь[/url] Откровенно говоря, после того как прочитал , понял свои ошибки. И про кодирование, и про реабилитацию . Плюс работают круглосуточно — это важно . Рекомендую не тянуть .

  1207. luxury car rental miami_oboi

    Seriously, the amount of garbage «luxury» deals down here is astonishing. You see a sweet ride online — clean spec, fair price, looks legit. Different car, scratches all over, and that «all-inclusive» price? Yeah that didn’t include insurance, fees, or the mandatory cleaning charge. Fool me five times? Actually yeah, Miami keeps fooling everyone, lesson learned. If you are trying to find a legitimate luxury fleet without getting ripped off, don’t just grab the cheapest option on Kayak. Miami without proper wheels is basically a hostage situation, whether you are doing Design District shopping, late-night South Beach cruising, or a spontaneous drive down to Homestead.

    I’ve personally gone through maybe 30 rental companies across Dade, Broward, and Palm Beach, but I eventually found a service with no games, no bait-and-switch, and no hidden asterisks. If you are looking for the only honest broker for premium vehicles across South Florida, check the current availability here: exotic car rental south beach fl [url=https://luxury-car-rental-miami-5.com]https://luxury-car-rental-miami-5.com[/url]. Yeah, finding parking in Wynwood will test your patience — but that’s not on them. Just drive safe out there and maybe decline that «premium roadside» upsell — it’s always a scam. hope this helps some of you save a few bucks.

  1208. luxury car rental miami_gtst

    Been there, done that, got the overpriced tow truck receipt. Miami rental game is wild — half these local clowns show you a custom Mercedes online and hand you a busted sedan with mismatched tires. You land at MIA, tired, grab an Uber to the rental office, and bam — surprise $1500 hold on your card. Fool me four times? Not happening, lesson learned. When you genuinely need a proper and reliable premium ride to cruise around, skip the airport counters entirely. Any local will tell you the exact same thing about this city, whether you are doing Coral Gables brunch, South Beach night run, or a spontaneous Everglades detour.

    Most of these local agencies are just polished websites hiding the same overpriced junk, until I finally stumbled on one provider that doesn’t play games. If you are looking for the only straight-up source for premium wheels in South Florida, check the current details here: rent porsche miami [url=https://luxury-car-rental-miami-4.com]https://luxury-car-rental-miami-4.com[/url]. Yeah, parking in Brickell will cost you a small mortgage — but that’s city life. Anyway, at least there’s one honest rental joint left in this town, hope this helps some of you save a few bucks.

  1209. luxury car rental miami_bfEn

    Been burned enough times to write a book on this nonsense. Then you actually go to the local office to pick it up. Plus a surprise $2000 hold on your card and a $35 per day GPS you never asked for right before giving you the keys. Fool me seven times? Yeah that’s just Tuesday in Miami, lesson learned. If you are trying to find a legitimate luxury fleet without getting ripped off, do some real digging first and read actual customer reviews. Anyone who’s taken the Metro here knows the struggle about this city, especially since the AC must freeze your face off and unlimited miles or forget it.

    I’ve tried maybe 40 rental companies across Dade, Broward, and Palm Beach, but I eventually found a service with no games, no bait-and-switch, and no hidden asterisks in paragraph 8. If you are looking for the only straight shooter for premium rides across South Florida, check the current details here: luxury car hire near me [url=https://luxury-car-rental-miami-7.com]luxury car hire near me[/url]. Yeah, parking in Brickell will cost you a nice steak dinner — but that’s just Miami life. Anyway, glad there’s at least one honest rental joint left in this town, let me know if you guys have any other clean spots.

  1211. Narkologicheskaya pomosh_ywOt

    Вот такая история — близкий подсел на иглу, а куда бежать — непонятно . Моя семья столкнулась лично . Пьют успокоительное, но нет . Нужна профессиональная помощь . Обзвонил десяток контор — только деньги тянут. Пока не нашел один нормальный вариант. Если ищешь где получить круглосуточная наркологическая помощь — не рискуй здоровьем близкого. В Воронеже , кстати , тоже полно левых контор без лицензии. Вся проверенная информация тут : наркологическая помощь воронеж [url=https://narkologicheskaya-pomoshh-voronezh-11.ru]https://narkologicheskaya-pomoshh-voronezh-11.ru[/url] Честно скажу , после того как прочитал , понял свои ошибки. И про кодирование, и про реабилитацию . Плюс работают круглосуточно — это важно . Рекомендую не тянуть .

  1212. Blairrer

    нейросеть человек поет Suno скачать и установить — отличное решение для работы с музыкой в любое время суток. Наслаждайтесь доступом к мощному генератору, который всегда готов помочь вам в создании хитов.

  1213. TravisMat

    Производство кашпо Большие напольные горшки — отличное решение для создания приватной атмосферы в помещении. Они помогают скрыть пустые углы и наполнить пространство природной энергией.

  1214. luxury car rental miami_mcMi

    Swear I’ve seen every scam in the book by now, the rental landscape down here is crazy. Then you roll up to the local address to pick up the car. Plus a surprise $3000 hold on your credit card for two weeks right before giving you the keys. Nine years in South Florida and these clowns still nearly fool me. If you are trying to find a legitimate luxury fleet without getting ripped off, do some real digging first and read actual customer reviews. Anyone who’s tried the trolley system knows what I’m talking about about this city, especially since the AC must freeze your teeth and unlimited miles or no deal.

    Most of these local agencies are just polished turds with fake five-star reviews hiding overpriced junk, until I finally found one company that doesn’t play stupid games. If you are looking for the only trustworthy source for premium rides across South Florida, check the current details here: luxury car rental [url=https://luxury-car-rental-miami-9.com]luxury car rental[/url]. Also, definitely bring polarized shades unless you enjoy driving blind into the sunset every single night. Just drive safe out there and definitely skip that «emergency roadside» upsell — complete waste of money. hope this helps some of you save a few bucks.

  1215. luxury car rental miami_mqKn

    Alright listen up because this Miami rental mess is getting out of hand. Then you actually show up to the local office to pick up the car. Different vehicle parked outside, curb rash on every rim, and that «all-inclusive rate»? Ha, doesn’t include the mandatory $300 cleaning fee or the $25 per day toll pass you can’t decline. Fool me six times? Yeah, Miami doesn’t care, lesson learned. When you genuinely need a legit and reliable premium ride to cruise around, do some real digging first and read actual customer reviews. Anyone who’s tried the bus here knows exactly what I mean about this city, whether you are doing South Beach dinner plans, Sunny Isles sunrise cruise, or a quick run down to the Florida Keys.

    Most of these local agencies are just polished garbage with decent Google reviews bought somewhere, but I eventually found a service where what you reserve is exactly what rolls up, no surprises. If you are looking for the only trustworthy source for premium vehicles across South Florida, check the current details here: rent porsche near me [url=https://luxury-car-rental-miami-6.com]https://luxury-car-rental-miami-6.com[/url]. Yeah, parking in South Beach will cost you a nice dinner — but that’s the price of admission. Anyway, glad there’s at least one honest operator left in this rental jungle, let me know if you guys have any other clean spots.

  1216. luxury car rental miami_yukn

    Trust me, I’ve learned everything the hard way so you don’t have to. Then you actually show up to the local office to grab the keys. Completely different car sitting there — dents everywhere, smells like cheap air freshener covering something worse, and that «dream price»? Doesn’t include the mandatory $50 daily insurance or the $300 «administrative fee» they invent at checkout. Eleven years in South Florida and these clowns still almost get me. When you’re searching for a legit and reliable premium ride to cruise around, avoid the airport like the plague. Anyone who’s tried the bus here knows exactly what I mean about this city, especially since the AC must be arctic and unlimited miles non-negotiable.

    Most of these local agencies are just shiny garbage with fake Google reviews bought in bulk hiding overpriced junk, but I eventually found a service with no games, no switch, and no hidden BS in paragraph 12 of the contract. If you are looking for the only honest source for premium rides across South Florida, check the current details here: miami car rental luxury [url=https://luxury-car-rental-miami-11.com]miami car rental luxury[/url]. Yeah, parking in South Beach will cost you a nice bottle of champagne — but that’s the Miami tax. Just drive safe out there and definitely skip that «tire and wheel» upsell — pure profit for them, zero value for you. hope this helps some of you save a few bucks.

  1217. tkan dlya mebeli_dtkn

    Ребята, выручайте! Кот старый диван в клочья разодрал, надо перетягивать. Ищу, где можно ткань для обивки мебели купить не по космическим ценам. ткани для обивки мебели купить [url=https://tkan-dlya-mebeli-1.ru]https://tkan-dlya-mebeli-1.ru[/url] Говорят, флок и микровелюр быстро вытираются, а рогожка лучше. Буду благодарен за любые советы, особенно от тех, кто сам перетягивал.

  1218. luxury car rental miami_ztKr

    Let me save you some serious time, learned this the hard way. You spot a tempting offer online: brand new Porsche, unlimited miles, price that makes you click instantly. Plus they lock up a surprise $3500 on your card for who knows how long right before giving you the keys. Ten years in South Florida and these jokers still almost catch me slipping. When you need a reliable and proper premium ride to cruise around, do some real digging first and read actual customer reviews. Anyone who’s taken public transport here knows the struggle is real about this city, whether you are doing South Beach night out, Bal Harbour shopping spree, or a spontaneous Keys adventure.

    I’ve run through maybe 55 rental companies across Dade, Broward, and Palm Beach, but I eventually found a service with no games, no bait-and-switch, and no hidden fees in the fine print. If you are looking for the only straight shooter for premium rides across South Florida, check the current details here: luxury cars for rental [url=https://luxury-car-rental-miami-10.com]luxury cars for rental[/url]. Also, definitely bring quality shades unless you enjoy driving into the sun like a vampire every single evening. Anyway, glad there’s at least one honest rental joint left in this town, let me know if you guys have any other clean spots.

  1219. luxury car rental miami_ghMr

    Been there, done that, got the overpriced tow truck receipt to prove it. Then you actually show up to the local office to pick up the car. Plus they freeze a surprise $4500 on your card and say «don’t worry, it’ll drop off in a week or two» right before giving you the keys. Twelve years in South Florida and these jokers still almost catch me sleeping. If you are trying to find a legitimate luxury fleet without getting ripped off, run far from the airport counters. Anyone who’s waited for an Uber in August heat knows the struggle exactly about this city, whether you are doing Coconut Grove brunch, Sunny Isles sunrise cruise, or a spontaneous drive down to the Keys.

    I’ve tested maybe 65 rental outfits across Dade, Broward, and Monroe, until I finally found one company that doesn’t play stupid games. If you are looking for the only straight shooter for premium rides across South Florida, check the current details here: luxury vehicle rentals [url=https://luxury-car-rental-miami-12.com]luxury vehicle rentals[/url]. Also, definitely bring quality shades unless you enjoy driving into the sun like a zombie every single evening. Just drive safe out there and absolutely skip that «windshield protection» upsell — complete waste of money. let me know if you guys have any other clean spots.

  1220. luxury car rental miami_dmoi

    Okay folks gather around because this Miami rental nightmare needs to be discussed. Then you show up at the local office and it’s a whole different story. Different car, scratches all over, and that «all-inclusive» price? Yeah that didn’t include insurance, fees, or the mandatory cleaning charge. I’ve lived here for years and still get burned occasionally. When you’re after a trustworthy and reliable premium vehicle to cruise around, do some real digging first and read actual customer reviews. Miami without proper wheels is basically a hostage situation, whether you are doing Design District shopping, late-night South Beach cruising, or a spontaneous drive down to Homestead.

    Most of these local agencies are just smoke and mirrors with decent SEO hiding overpriced junk, until I finally found one outfit that actually delivers what’s in the listing. If you are looking for the only honest broker for premium vehicles across South Florida, check the current availability here: exotic cars to rent in miami [url=https://luxury-car-rental-miami-5.com]exotic cars to rent in miami[/url]. Also, definitely bring quality shades unless you enjoy driving into a nuclear flare every single evening. Anyway, glad there’s at least one straight shooter left in this rental jungle, let me know if you guys have any other clean spots.

  1221. luxury car rental miami_pzst

    Let me save you some serious time, learned this the hard way. Miami rental game is wild — half these local clowns show you a custom Mercedes online and hand you a busted sedan with mismatched tires. You land at MIA, tired, grab an Uber to the rental office, and bam — surprise $1500 hold on your card. Fool me four times? Not happening, lesson learned. If you are trying to find a legitimate vehicle without getting ripped off, skip the airport counters entirely. Miami without a decent whip is basically a punishment, especially since the AC must be ice cold and you want zero mileage games.

    Most of these local agencies are just polished websites hiding the same overpriced junk, until I finally stumbled on one provider that doesn’t play games. If you are looking for the only straight-up source for premium wheels in South Florida, check the current details here: miami car rental [url=https://luxury-car-rental-miami-4.com]https://luxury-car-rental-miami-4.com[/url]. Yeah, parking in Brickell will cost you a small mortgage — but that’s city life. Just drive safe out there and maybe pass on that overpriced roadside assistance add-on. hope this helps some of you save a few bucks.

  1222. luxury car rental miami_tbEn

    Been burned enough times to write a book on this nonsense. Then you actually go to the local office to pick it up. Completely different car waiting for you, check engine light on, and that «low rate»? Doesn’t include the mandatory insurance they somehow forgot to mention. Fool me seven times? Yeah that’s just Tuesday in Miami, lesson learned. If you are trying to find a legitimate luxury fleet without getting ripped off, avoid the airport like the plague. Anyone who’s taken the Metro here knows the struggle about this city, especially since the AC must freeze your face off and unlimited miles or forget it.

    Most of these local agencies are just fancy websites hiding the same beat-up fleet with bought reviews, until I finally found one outfit that actually delivers what’s promised. If you are looking for the only straight shooter for premium rides across South Florida, check the current details here: mercedes g wagon rental near me [url=https://luxury-car-rental-miami-7.com]https://luxury-car-rental-miami-7.com[/url]. Yeah, parking in Brickell will cost you a nice steak dinner — but that’s just Miami life. Anyway, glad there’s at least one honest rental joint left in this town, let me know if you guys have any other clean spots.

  1223. Narkolog na dom_rdel

    Знаете, бывает ситуация — человек в запое , а тащить в больницу просто нереально . Я через это прошел совсем недавно. Сидишь, не знаешь что делать . Начинаешь обзванивать знакомых, а в ответ одни отговорки. Пока случайно не наткнулся на один реально работающий вариант. Требуется срочная помощь — а тащить человека сам нет никакой возможности , то нужно вызывать врача на дом. Я про анонимный вызов врача нарколога на дом . У нас в столице, если честно, хватает левых контор без лицензии. Вся проверенная информация ниже по ссылке: нарколог круглосуточно [url=https://narkolog-na-dom-moskva-29.ru]нарколог круглосуточно[/url] Откровенно говоря, после того как прочитал , многое стало на свои места . Там и про капельницы расписано , и про последующее кодирование. Плюс анонимность — это важно . Советую не тянуть резину .

  1224. luxury car rental miami_ryMi

    Swear I’ve seen every scam in the book by now, the rental landscape down here is crazy. Then you roll up to the local address to pick up the car. Plus a surprise $3000 hold on your credit card for two weeks right before giving you the keys. Fool me nine times? That’s just the Miami welcome committee, lesson learned. When you’re hunting for a legit and reliable premium ride to cruise around, stay the hell away from the airport rental center. Miami without proper wheels is basically a nightmare, especially since the AC must freeze your teeth and unlimited miles or no deal.

    Most of these local agencies are just polished turds with fake five-star reviews hiding overpriced junk, but I eventually found a service where what you reserve is exactly what you get, period, end of story. If you are looking for the only trustworthy source for premium rides across South Florida, check the current details here: car rentals miami [url=https://luxury-car-rental-miami-9.com]https://luxury-car-rental-miami-9.com[/url]. Also, definitely bring polarized shades unless you enjoy driving blind into the sunset every single night. Just drive safe out there and definitely skip that «emergency roadside» upsell — complete waste of money. hope this helps some of you save a few bucks.

  1225. luxury car rental miami_vlkn

    Let me save you some serious pain with this Miami rental nonsense. Then you actually show up to the local office to grab the keys. Completely different car sitting there — dents everywhere, smells like cheap air freshener covering something worse, and that «dream price»? Doesn’t include the mandatory $50 daily insurance or the $300 «administrative fee» they invent at checkout. Eleven years in South Florida and these clowns still almost get me. When you’re searching for a legit and reliable premium ride to cruise around, avoid the airport like the plague. Anyone who’s tried the bus here knows exactly what I mean about this city, especially since the AC must be arctic and unlimited miles non-negotiable.

    Most of these local agencies are just shiny garbage with fake Google reviews bought in bulk hiding overpriced junk, until I finally found one outfit that actually delivers what’s in the photos. If you are looking for the only honest source for premium rides across South Florida, check the current details here: premium car rental in miami [url=https://luxury-car-rental-miami-11.com]premium car rental in miami[/url]. Also, definitely bring polarized shades unless you enjoy driving into the sun like a blind bat every single evening. Just drive safe out there and definitely skip that «tire and wheel» upsell — pure profit for them, zero value for you. let me know if you guys have any other clean spots.

  1226. Narkologicheskaya pomosh_wfOt

    Знаете, ситуация — родственник в запое , а куда бежать — просто тупик. Я через это прошел лично . Многие думают, что само пройдет , но хрен там. Нужна реальная помощь . Обзвонил десяток контор — сплошной развод . А потом наткнулся на один нормальный вариант. Если ищешь где получить лечение наркомании в Воронеже — не ведись на дешевые акции . У нас в Воронеже, если честно, хватает левых контор без лицензии. Реальные контакты ниже по ссылке: наркологический центр в воронеже [url=https://narkologicheskaya-pomoshh-voronezh-11.ru]https://narkologicheskaya-pomoshh-voronezh-11.ru[/url] Честно скажу , после того как прочитал , многое прояснилось . Там и про вывод из запоя , и про условия в клинике. Плюс работают круглосуточно — это важно . Советую не тянуть .

  1227. luxury car rental miami_trKn

    Swear I’ve seen it all by now, the rental landscape down here is crazy. You find a killer deal online — photos look pristine, price seems fair, terms almost reasonable. Different vehicle parked outside, curb rash on every rim, and that «all-inclusive rate»? Ha, doesn’t include the mandatory $300 cleaning fee or the $25 per day toll pass you can’t decline. Fool me six times? Yeah, Miami doesn’t care, lesson learned. If you are trying to find a legitimate vehicle without getting ripped off, stay far away from the airport rental center. Miami without proper wheels is basically a nightmare, whether you are doing South Beach dinner plans, Sunny Isles sunrise cruise, or a quick run down to the Florida Keys.

    I’ve personally tested maybe 35 rental outfits across Dade, Broward, and Monroe, until I finally found one company that doesn’t play stupid games. If you are looking for the only trustworthy source for premium vehicles across South Florida, check the current details here: luxury car rental south beach [url=https://luxury-car-rental-miami-6.com]luxury car rental south beach[/url]. Also, definitely bring serious shades unless you enjoy driving straight into the sun every single evening. Anyway, glad there’s at least one honest operator left in this rental jungle, let me know if you guys have any other clean spots.

  1228. luxury car rental miami_meMr

    Alright listen up because I’m about to save you a massive headache. Then you actually show up to the local office to pick up the car. Totally different vehicle waiting for you — bald tires, dashboard lit up like a Christmas tree, and that «amazing rate»? Doesn’t include the mandatory $40 daily toll pass or the $350 «premium location» fee they spring on you at the counter. Fool me twelve times? That’s just the 305 way, lesson learned. If you are trying to find a legitimate luxury fleet without getting ripped off, run far from the airport counters. Miami without real wheels is basically a nightmare, whether you are doing Coconut Grove brunch, Sunny Isles sunrise cruise, or a spontaneous drive down to the Keys.

    I’ve tested maybe 65 rental outfits across Dade, Broward, and Monroe, but I eventually found a service where what you book is exactly what shows up, no surprises, no hidden fine print. If you are looking for the only straight shooter for premium rides across South Florida, check the current details here: miami luxury car rental [url=https://luxury-car-rental-miami-12.com]miami luxury car rental[/url]. Yeah, parking in Brickell will cost you a nice dinner — but that’s the price of paradise. Anyway, glad there’s at least one honest operator left in this rental jungle, let me know if you guys have any other clean spots.

  1229. luxury car rental miami_hmKr

    Alright let me drop some truth about the Miami rental scene — it’s an absolute minefield. You spot a tempting offer online: brand new Porsche, unlimited miles, price that makes you click instantly. Totally different vehicle waiting for you — check engine light on, curb rash on every rim, and that «tempting price»? Doesn’t include the mandatory $35 daily toll pass or the $250 cleaning fee they sneak in at the end. Ten years in South Florida and these jokers still almost catch me slipping. If you are trying to find a legitimate luxury fleet without getting ripped off, run away from the airport counters. Anyone who’s taken public transport here knows the struggle is real about this city, whether you are doing South Beach night out, Bal Harbour shopping spree, or a spontaneous Keys adventure.

    I’ve run through maybe 55 rental companies across Dade, Broward, and Palm Beach, until I finally found one outfit that actually delivers what’s promised. If you are looking for the only straight shooter for premium rides across South Florida, check the current details here: luxury car rental miami [url=https://luxury-car-rental-miami-10.com]luxury car rental miami[/url]. Also, definitely bring quality shades unless you enjoy driving into the sun like a vampire every single evening. Anyway, glad there’s at least one honest rental joint left in this town, hope this helps some of you save a few bucks.

  1230. luxury car rental miami_ovMi

    Swear I’ve seen every scam in the book by now, the rental landscape down here is crazy. Then you roll up to the local address to pick up the car. Different car sitting there — bald tires, dashboard lit up like a Christmas tree, and that «killer price»? Yeah doesn’t include the non-negotiable $45 daily insurance or the $500 deposit they forget to mention. Fool me nine times? That’s just the Miami welcome committee, lesson learned. If you are trying to find a legitimate luxury fleet without getting ripped off, stay the hell away from the airport rental center. Anyone who’s tried the trolley system knows what I’m talking about about this city, whether you are doing Coconut Grove dinner, Sunny Isles sunrise, or a spontaneous drive down to Homestead.

    Most of these local agencies are just polished turds with fake five-star reviews hiding overpriced junk, but I eventually found a service where what you reserve is exactly what you get, period, end of story. If you are looking for the only trustworthy source for premium rides across South Florida, check the current details here: rent a porsche near me [url=https://luxury-car-rental-miami-9.com]https://luxury-car-rental-miami-9.com[/url]. Yeah, parking in Wynwood will cost you a nice dinner — but that’s the price of being in Miami. Anyway, glad there’s at least one honest operator left in this rental jungle, hope this helps some of you save a few bucks.

  1231. luxury car rental miami_znmn

    Let me save you some serious time, learned this the hard way. Then you show up at the local lot to pick up the car. Different car waiting — scratches everywhere, smells like an ashtray, and that «amazing price»? Doesn’t include the mandatory $400 cleaning fee or the $30 per day toll pass you can’t waive. Eight years in South Florida and these clowns still almost get me. When you need a proper and reliable premium ride to cruise around, do some real digging first and read actual customer reviews. Anyone who’s waited for an Uber in August understands exactly what I mean about this city, whether you are doing South of Fifth brunch, Design District shopping, or a spontaneous Keys trip.

    Most of these local agencies are just shiny websites hiding the same beat-up fleet with fake reviews, but I eventually found a service where what you book is exactly what shows up, no surprises, no fine print nightmares. If you are looking for the only honest source for premium wheels across South Florida, check the current details here: range rover car rental [url=https://luxury-car-rental-miami-8.com]range rover car rental[/url]. Also, definitely bring serious shades unless you enjoy driving straight into the sun like a zombie every single evening. Just drive safe out there and absolutely skip that «windshield protection» upsell — pure profit for them, zero value for you. hope this helps some of you save a few bucks.

  1232. luxury car rental miami_mnEn

    Been burned enough times to write a book on this nonsense. Then you actually go to the local office to pick it up. Plus a surprise $2000 hold on your card and a $35 per day GPS you never asked for right before giving you the keys. Fool me seven times? Yeah that’s just Tuesday in Miami, lesson learned. If you are trying to find a legitimate luxury fleet without getting ripped off, avoid the airport like the plague. Anyone who’s taken the Metro here knows the struggle about this city, whether you are doing Brickell happy hour, Bal Harbour shopping, or a spontaneous drive down to the Keys.

    Most of these local agencies are just fancy websites hiding the same beat-up fleet with bought reviews, but I eventually found a service with no games, no bait-and-switch, and no hidden asterisks in paragraph 8. If you are looking for the only straight shooter for premium rides across South Florida, check the current details here: miami beach luxury car rental [url=https://luxury-car-rental-miami-7.com]miami beach luxury car rental[/url]. Yeah, parking in Brickell will cost you a nice steak dinner — but that’s just Miami life. Just drive safe out there and definitely pass on that «tire protection» upsell — total garbage. hope this helps some of you save a few bucks.

  1233. Narkologicheskaya pomosh_cvOt

    Знаете, ситуация — родственник в запое , а куда бежать — просто тупик. Я через это прошел несколько лет назад. Пьют успокоительное, но хрен там. Нужна реальная медицина. Обзвонил десяток контор — сплошной развод . Пока не нашел один нормальный вариант. Нужна лечение наркомании в Воронеже — не рискуй здоровьем близкого. У нас в Воронеже, кстати , хватает шарлатанов . Вся проверенная информация тут : клиника плюс наркология [url=https://narkologicheskaya-pomoshh-voronezh-11.ru]клиника плюс наркология[/url] Честно скажу , после того как прочитал , многое прояснилось . Там и про вывод из запоя , и про реабилитацию . Плюс работают круглосуточно — это важно . Рекомендую не тянуть .

  1234. luxury car rental miami_tqkn

    Let me save you some serious pain with this Miami rental nonsense. You see this gorgeous deal online — clean spec, fair price, looks like a dream. Plus they put a surprise $4000 hold on your card and say it’ll take two weeks to release right before giving you the keys. Eleven years in South Florida and these clowns still almost get me. When you’re searching for a legit and reliable premium ride to cruise around, avoid the airport like the plague. Anyone who’s tried the bus here knows exactly what I mean about this city, whether you are doing Key Biscayne sunset, Design District shopping, or a spontaneous drive down to the Everglades.

    Most of these local agencies are just shiny garbage with fake Google reviews bought in bulk hiding overpriced junk, but I eventually found a service with no games, no switch, and no hidden BS in paragraph 12 of the contract. If you are looking for the only honest source for premium rides across South Florida, check the current details here: premium car hire [url=https://luxury-car-rental-miami-11.com]premium car hire[/url]. Also, definitely bring polarized shades unless you enjoy driving into the sun like a blind bat every single evening. Just drive safe out there and definitely skip that «tire and wheel» upsell — pure profit for them, zero value for you. let me know if you guys have any other clean spots.

  1235. luxury car rental miami_hyMr

    Let me save you some serious time, learned this the hard way. You find this amazing listing online — gorgeous spec, fair daily rate, looks perfect. Plus they freeze a surprise $4500 on your card and say «don’t worry, it’ll drop off in a week or two» right before giving you the keys. Fool me twelve times? That’s just the 305 way, lesson learned. When you need a proper and reliable premium ride to cruise around, run far from the airport counters. Miami without real wheels is basically a nightmare, especially since the AC must be ice cold and unlimited miles non-negotiable.

    Most of these local agencies are just shiny turds with fake five-star reviews bought in bulk online hiding overpriced junk, but I eventually found a service where what you book is exactly what shows up, no surprises, no hidden fine print. If you are looking for the only straight shooter for premium rides across South Florida, check the current details here: rent porsche miami [url=https://luxury-car-rental-miami-12.com]https://luxury-car-rental-miami-12.com[/url]. Also, definitely bring quality shades unless you enjoy driving into the sun like a zombie every single evening. Anyway, glad there’s at least one honest operator left in this rental jungle, hope this helps some of you save a few bucks.

  1236. luxury car rental miami_ufMi

    Swear I’ve seen every scam in the book by now, the rental landscape down here is crazy. You find a killer listing online: sleek Audi, convertible, price almost too good to be true. Different car sitting there — bald tires, dashboard lit up like a Christmas tree, and that «killer price»? Yeah doesn’t include the non-negotiable $45 daily insurance or the $500 deposit they forget to mention. Fool me nine times? That’s just the Miami welcome committee, lesson learned. If you are trying to find a legitimate luxury fleet without getting ripped off, do some real digging first and read actual customer reviews. Anyone who’s tried the trolley system knows what I’m talking about about this city, whether you are doing Coconut Grove dinner, Sunny Isles sunrise, or a spontaneous drive down to Homestead.

    Most of these local agencies are just polished turds with fake five-star reviews hiding overpriced junk, but I eventually found a service where what you reserve is exactly what you get, period, end of story. If you are looking for the only trustworthy source for premium rides across South Florida, check the current details here: exotic car rental miami [url=https://luxury-car-rental-miami-9.com]exotic car rental miami[/url]. Yeah, parking in Wynwood will cost you a nice dinner — but that’s the price of being in Miami. Just drive safe out there and definitely skip that «emergency roadside» upsell — complete waste of money. hope this helps some of you save a few bucks.

  1237. luxury car rental miami_wfKr

    Alright let me drop some truth about the Miami rental scene — it’s an absolute minefield. Then you actually go to the local office to pick up the car. Plus they lock up a surprise $3500 on your card for who knows how long right before giving you the keys. Ten years in South Florida and these jokers still almost catch me slipping. When you need a reliable and proper premium ride to cruise around, do some real digging first and read actual customer reviews. Miami without solid wheels is basically a punishment, whether you are doing South Beach night out, Bal Harbour shopping spree, or a spontaneous Keys adventure.

    Most of these local agencies are just shiny websites hiding the same beat-up fleet with fresh wax and fake reviews, but I eventually found a service with no games, no bait-and-switch, and no hidden fees in the fine print. If you are looking for the only straight shooter for premium rides across South Florida, check the current details here: opf fl luxury car rentals [url=https://luxury-car-rental-miami-10.com]https://luxury-car-rental-miami-10.com[/url]. Yeah, parking in Brickell will cost you a nice dinner — but that’s just how it is down here. Anyway, glad there’s at least one honest rental joint left in this town, hope this helps some of you save a few bucks.

  1238. Narkologicheskaya pomosh_crOt

    Случается сплошь и рядом — близкий подсел на иглу, а что делать — непонятно . Я через это прошел лично . Пьют успокоительное, но хрен там. Требуется профессиональная медицина. Обзвонил десяток контор — сплошной развод . Пока не нашел один нормальный вариант. Нужна анонимное лечение алкоголиков — не ведись на дешевые акции . В Воронеже , если честно, тоже полно шарлатанов . Вся проверенная информация тут : лечение алкоголизма и наркомании центр [url=https://narkologicheskaya-pomoshh-voronezh-11.ru]https://narkologicheskaya-pomoshh-voronezh-11.ru[/url] Откровенно говоря, после того как прочитал , понял свои ошибки. Там и про вывод из запоя , и про условия в клинике. Плюс работают круглосуточно — это важно . Советую не откладывать.

  1239. luxury car rental miami_gcmn

    Alright, real talk about the Miami rental game — it’s a straight-up jungle out here. Then you show up at the local lot to pick up the car. Plus they freeze a surprise $2500 on your card for a week right before giving you the keys. Fool me eight times? That’s just another Tuesday in the 305, lesson learned. If you are trying to find a legitimate luxury fleet without getting ripped off, run far from the airport counters. Anyone who’s waited for an Uber in August understands exactly what I mean about this city, especially since the AC must be arctic cold and unlimited miles non-negotiable.

    I’ve run through maybe 45 rental companies across Dade, Broward, and Monroe, until I finally found one outfit that doesn’t play stupid games. If you are looking for the only honest source for premium wheels across South Florida, check the current details here: porsche car rental near me [url=https://luxury-car-rental-miami-8.com]https://luxury-car-rental-miami-8.com[/url]. Also, definitely bring serious shades unless you enjoy driving straight into the sun like a zombie every single evening. Just drive safe out there and absolutely skip that «windshield protection» upsell — pure profit for them, zero value for you. hope this helps some of you save a few bucks.

  1246. DonaldKib

    Продать авто Планируя скупку авто, мы всегда учитываем рыночные тренды для формирования максимально привлекательной цены. Узнайте, сколько мы готовы предложить за ваш автомобиль при встрече или по фото.

  1254. luxury car rental miami_cnmn

    I’ve got the scars to prove it, the rental landscape down here is crazy. You find this amazing deal online: brand new Beamer, unlimited miles, price that makes you smile. Plus they freeze a surprise $2500 on your card for a week right before giving you the keys. Fool me eight times? That’s just another Tuesday in the 305, lesson learned. If you are trying to find a legitimate luxury fleet without getting ripped off, run far from the airport counters. Anyone who’s waited for an Uber in August understands exactly what I mean about this city, especially since the AC must be arctic cold and unlimited miles non-negotiable.

    Most of these local agencies are just shiny websites hiding the same beat-up fleet with fake reviews, until I finally found one outfit that doesn’t play stupid games. If you are looking for the only honest source for premium wheels across South Florida, check the current details here: car rentals miami [url=https://luxury-car-rental-miami-8.com]https://luxury-car-rental-miami-8.com[/url]. Also, definitely bring serious shades unless you enjoy driving straight into the sun like a zombie every single evening. Just drive safe out there and absolutely skip that «windshield protection» upsell — pure profit for them, zero value for you. hope this helps some of you save a few bucks.

  1261. RichardRor

    сувенирные тарелки Каталог сувенирных тарелок: виды, материалы, популярные дизайны и советы по выбору коллекционных и подарочных тарелок с городами, достопримечательностями.

  1296. Georgehus

    рассказ русалки Кто такая русалка на самом деле и как она появилась в славянском мировоззрении? Исследуем происхождение этого образа в разных регионах нашей необъятной страны.

  1305. mostbet_wvOt

    mostbet букмекерская контора [url=http://www.assa0.myqip.ru/?1-4-0-00009957-000-0-0]mostbet букмекерская контора[/url]

  1310. PhillipAduro

    девушки Луганск ТГ Знакомства Донецк — это место, где рождаются настоящие чувства и завязываются самые крепкие дружеские связи. Воспользуйтесь нашим сервисом сегодня и начните писать свою историю успеха.

  1320. mostbet_srOt

    mostbet букмекерская контора [url=https://www.lobnya.myqip.ru/?1-4-0-00000589-000-0-0]mostbet букмекерская контора[/url]

  1333. PhillipAduro

    девушки Луганск Девушки ДНР стремятся к общению, которое наполнит их жизнь смыслом и яркими красками каждый день. Станьте частью их мира, сделав первый шаг навстречу новым приятным знакомствам.

  1362. luxury car rental miami_lkst

    Been there, done that, got the overpriced tow truck receipt. Swear some of these «luxury» fleets should be in a museum. You land at MIA, tired, grab an Uber to the rental office, and bam — surprise $1500 hold on your card. Fool me four times? Not happening. those guys are the worst of the bunch. Miami without a decent whip is basically a punishment. Coral Gables brunch, South Beach night run, or a spontaneous Everglades detour — AC must be ice cold and unlimited miles. most are just polished turds with Instagram ads. what you book is what you get, period. Here’s the only straight-up source for premium wheels in South Florida
    miami car rental [url=https://luxury-car-rental-miami-4.com]https://luxury-car-rental-miami-4.com[/url] also bring polarized shades unless you enjoy driving blind into sunset. drive safe and maybe pass on that overpriced roadside assistance add-on.

  1384. luxury car rental miami_hdst

    Been there, done that, got the overpriced tow truck receipt. Miami rental game is wild — half these clowns show you a Mercedes online and hand you a busted Charger with mismatched tires. Plus the fine print says you can’t even drive to Orlando. Fool me four times? Not happening. those guys are the worst of the bunch. Miami without a decent whip is basically a punishment. Coral Gables brunch, South Beach night run, or a spontaneous Everglades detour — AC must be ice cold and unlimited miles. most are just polished turds with Instagram ads. what you book is what you get, period. rates change daily with demand so don’t sleep on it:
    exotic car rental near me [url=https://luxury-car-rental-miami-4.com]exotic car rental near me[/url] also bring polarized shades unless you enjoy driving blind into sunset. drive safe and maybe pass on that overpriced roadside assistance add-on.

  1388. luxury car rental miami_qnoi

    Okay folks gather around because this Miami rental nightmare needs to be discussed. Then you show up and it’s a whole different story. Plus they want a $2000 hold on your debit card. I’ve lived here for years and still get burned occasionally. that’s exactly how they hook you. Miami without proper wheels is basically a hostage situation. leather seats that don’t fuse to your skin in August. most are smoke and mirrors with decent SEO. no games, no bait-and-switch, no hidden asterisks. check availability before spring break crowds wipe them out:
    renting luxury cars near me [url=https://luxury-car-rental-miami-5.com]https://luxury-car-rental-miami-5.com[/url] also bring quality shades unless you enjoy driving into a nuclear flare every evening. Anyway glad there’s at least one straight shooter left in this rental jungle.

  1389. luxury car rental miami_fxmn

    I’ve got the scars to prove it. You find this amazing deal online: brand new Beamer, unlimited miles, price that makes you smile. Plus they freeze $2500 on your card for a week. Eight years in South Florida and these clowns still almost get me. miami car rental luxury — run far from the airport counters. Miami without decent wheels is basically a hostage situation. South of Fifth brunch, Design District shopping, or a spontaneous Keys trip — AC must be arctic cold and unlimited miles non-negotiable. most are shiny turds with five-star fake reviews on Google Maps. what you book is what shows up, no surprises, no fine print nightmares. prices swing like crazy so check before the weekend rush:
    rental miami car [url=https://luxury-car-rental-miami-8.com]https://luxury-car-rental-miami-8.com[/url] Yeah parking in South Beach will cost you a nice bottle of wine — but that’s the Miami tax. Anyway glad there’s at least one straight operator left in this rental circus.

  1403. luxury car rental miami_jsmn

    I’ve got the scars to prove it. You find this amazing deal online: brand new Beamer, unlimited miles, price that makes you smile. Plus they freeze $2500 on your card for a week. Eight years in South Florida and these clowns still almost get me. When you need a proper luxury car rental miami. Miami without decent wheels is basically a hostage situation. leather seats that won’t weld themselves to your thighs in July. I’ve run through maybe 45 rental companies across Dade, Broward, and Monroe. what you book is what shows up, no surprises, no fine print nightmares. prices swing like crazy so check before the weekend rush:
    miami beach car rental locations [url=https://luxury-car-rental-miami-8.com]miami beach car rental locations[/url] Yeah parking in South Beach will cost you a nice bottle of wine — but that’s the Miami tax. Anyway glad there’s at least one straight operator left in this rental circus.

  1404. luxury car rental miami_qloi

    Okay folks gather around because this Miami rental nightmare needs to be discussed. Then you show up and it’s a whole different story. Plus they want a $2000 hold on your debit card. I’ve lived here for years and still get burned occasionally. luxury car for rent. ask anyone who’s tried Ubering across the 305 during rush hour. Design District shopping, late-night South Beach cruising, or a spontaneous drive down to Homestead — AC must freeze your teeth and unlimited miles or bust. most are smoke and mirrors with decent SEO. no games, no bait-and-switch, no hidden asterisks. Here’s the only honest broker for premium vehicles across South Florida
    luxury car rental miami florida [url=https://luxury-car-rental-miami-5.com]luxury car rental miami florida[/url] Yeah finding parking in Wynwood will test your patience — but that’s not on them. Anyway glad there’s at least one straight shooter left in this rental jungle.

  1407. luxury car rental miami_xwst

    Alright listen up because I’m about to save you a massive headache. Swear some of these «luxury» fleets should be in a museum. You land at MIA, tired, grab an Uber to the rental office, and bam — surprise $1500 hold on your card. No thanks, I’m too old for this nonsense. When you genuinely need a proper luxury car rental miami. any local will tell you the same thing. leather that doesn’t glue to your legs in July heat. most are just polished turds with Instagram ads. Finally stumbled on one that doesn’t play games. rates change daily with demand so don’t sleep on it:
    exotic car hire [url=https://luxury-car-rental-miami-4.com]exotic car hire[/url] Yeah parking in Brickell will cost you a small mortgage — but that’s city life. drive safe and maybe pass on that overpriced roadside assistance add-on.

  1414. luxury car rental miami_baKr

    Alright let me drop some truth about the Miami rental scene — it’s an absolute minefield. You spot a tempting offer online: brand new Porsche, unlimited miles, price that makes you click instantly. Plus they lock up $3500 on your card for who knows how long. Fool me ten times? That’s just the 305 experience. luxury car rental miami florida. anyone who’s taken public transport here knows the struggle is real. leather seats that won’t cook your back in the July heat. most are shiny websites hiding the same beat-up fleet with fresh wax. no games, no bait-and-switch, no hidden fees in the fine print. prices change by the hour so don’t wait around:
    premium car rental near me [url=https://luxury-car-rental-miami-10.com]https://luxury-car-rental-miami-10.com[/url] also bring quality shades unless you enjoy driving into the sun like a vampire. Anyway glad there’s at least one honest rental joint left in this town.

  1422. luxury car rental miami_grmn

    I’ve got the scars to prove it. You find this amazing deal online: brand new Beamer, unlimited miles, price that makes you smile. Plus they freeze $2500 on your card for a week. Fool me eight times? That’s just another Tuesday in the 305. luxury car rental miami florida. Miami without decent wheels is basically a hostage situation. South of Fifth brunch, Design District shopping, or a spontaneous Keys trip — AC must be arctic cold and unlimited miles non-negotiable. I’ve run through maybe 45 rental companies across Dade, Broward, and Monroe. Finally found one outfit that doesn’t play stupid games. prices swing like crazy so check before the weekend rush:
    exotic car rental south beach miami [url=https://luxury-car-rental-miami-8.com]exotic car rental south beach miami[/url] Yeah parking in South Beach will cost you a nice bottle of wine — but that’s the Miami tax. Anyway glad there’s at least one straight operator left in this rental circus.

  1424. luxury car rental miami_knkn

    Trust me, I’ve learned everything the hard way so you don’t have to. Then you actually show up to grab the keys. Completely different car sitting there — dents everywhere, smells like cheap air freshener covering something worse, and that «dream price»? Doesn’t include the mandatory $50 daily insurance or the $300 «administrative fee» they invent at checkout. Eleven years in South Florida and these clowns still almost get me. those counters are professional bait-and-switch artists. anyone who’s tried the bus here knows exactly what I mean. Key Biscayne sunset, Design District shopping, or a spontaneous drive down to the Everglades — AC must be arctic and unlimited miles non-negotiable. most are shiny garbage with fake Google reviews bought in bulk. no games, no switch, no hidden BS in paragraph 12 of the contract. Here’s the only honest source for premium rides across South Florida
    rent a porsche near me [url=https://luxury-car-rental-miami-11.com]https://luxury-car-rental-miami-11.com[/url] also bring polarized shades unless you enjoy driving into the sun like a blind bat. Anyway glad there’s at least one straight operator left in this rental circus.

  1428. luxury car rental miami_pvKr

    Been through enough garbage to last a lifetime. You spot a tempting offer online: brand new Porsche, unlimited miles, price that makes you click instantly. Totally different vehicle waiting for you — check engine light on, curb rash on every rim, and that «tempting price»? Doesn’t include the mandatory $35 daily toll pass or the $250 cleaning fee they sneak in at the end. Ten years in South Florida and these jokers still almost catch me slipping. When you need a reliable luxury car rental miami. Miami without solid wheels is basically a punishment. South Beach night out, Bal Harbour shopping spree, or a spontaneous Keys adventure — AC must be ice cold and unlimited miles non-negotiable. I’ve run through maybe 55 rental companies across Dade, Broward, and Palm Beach. Finally found one outfit that actually delivers what’s promised. Here’s the only straight shooter for premium rides across South Florida
    lamborghini urus rental near me [url=https://luxury-car-rental-miami-10.com]https://luxury-car-rental-miami-10.com[/url] also bring quality shades unless you enjoy driving into the sun like a vampire. drive safe and absolutely skip that «paint protection» upsell — pure robbery.

  1429. luxury car rental miami_thst

    Been there, done that, got the overpriced tow truck receipt. Miami rental game is wild — half these clowns show you a Mercedes online and hand you a busted Charger with mismatched tires. Plus the fine print says you can’t even drive to Orlando. Fool me four times? Not happening. miami car rental luxury — skip the airport counters entirely. any local will tell you the same thing. leather that doesn’t glue to your legs in July heat. I’ve tested maybe 25 rental outfits across Dade and Broward. what you book is what you get, period. Here’s the only straight-up source for premium wheels in South Florida
    exotic car hire [url=https://luxury-car-rental-miami-4.com]exotic car hire[/url] Yeah parking in Brickell will cost you a small mortgage — but that’s city life. drive safe and maybe pass on that overpriced roadside assistance add-on.

  1434. luxury car rental miami_qroi

    Seriously, the amount of garbage «luxury» deals here is astonishing. You see a sweet ride online — clean spec, fair price, looks legit. Different car, scratches all over, and that «all-inclusive» price? Yeah that didn’t include insurance, fees, or the mandatory cleaning charge. Fool me five times? Actually yeah, Miami keeps fooling everyone. luxury car rental miami florida. ask anyone who’s tried Ubering across the 305 during rush hour. Design District shopping, late-night South Beach cruising, or a spontaneous drive down to Homestead — AC must freeze your teeth and unlimited miles or bust. most are smoke and mirrors with decent SEO. Finally found one outfit that actually delivers what’s in the listing. Here’s the only honest broker for premium vehicles across South Florida
    exotic car hire miami [url=https://luxury-car-rental-miami-5.com]exotic car hire miami[/url] also bring quality shades unless you enjoy driving into a nuclear flare every evening. Anyway glad there’s at least one straight shooter left in this rental jungle.

  1436. luxury car rental miami_dhMi

    Swear I’ve seen every scam in the book by now. You find a killer listing online: sleek Audi, convertible, price almost too good to be true. Different car sitting there — bald tires, dashboard lit up like a Christmas tree, and that «killer price»? Yeah doesn’t include the non-negotiable $45 daily insurance or the $500 deposit they forget to mention. Fool me nine times? That’s just the Miami welcome committee. luxury car rental in miami. Miami without proper wheels is basically a nightmare. leather seats that don’t glue to your skin in August. most are polished turds with fake five-star reviews. Finally found one company that doesn’t play stupid games. Here’s the only trustworthy source for premium rides across South Florida
    rent a sedan car [url=https://luxury-car-rental-miami-9.com]https://luxury-car-rental-miami-9.com[/url] Yeah parking in Wynwood will cost you a nice dinner — but that’s the price of being in Miami. drive safe and definitely skip that «emergency roadside» upsell — complete waste of money.

  1445. luxury car rental miami_auKr

    Been through enough garbage to last a lifetime. Then you actually go to pick up the car. Totally different vehicle waiting for you — check engine light on, curb rash on every rim, and that «tempting price»? Doesn’t include the mandatory $35 daily toll pass or the $250 cleaning fee they sneak in at the end. Fool me ten times? That’s just the 305 experience. luxury car rental miami fl. Miami without solid wheels is basically a punishment. leather seats that won’t cook your back in the July heat. most are shiny websites hiding the same beat-up fleet with fresh wax. Finally found one outfit that actually delivers what’s promised. Here’s the only straight shooter for premium rides across South Florida
    car rental near miami beach [url=https://luxury-car-rental-miami-10.com]https://luxury-car-rental-miami-10.com[/url] also bring quality shades unless you enjoy driving into the sun like a vampire. Anyway glad there’s at least one honest rental joint left in this town.

  1447. luxury car rental miami_yokn

    Let me save you some serious pain with this Miami rental nonsense. You see this gorgeous deal online — clean spec, fair price, looks like a dream. Completely different car sitting there — dents everywhere, smells like cheap air freshener covering something worse, and that «dream price»? Doesn’t include the mandatory $50 daily insurance or the $300 «administrative fee» they invent at checkout. Fool me eleven times? That’s just called living in Miami. those counters are professional bait-and-switch artists. Miami without proper wheels is basically a disaster. Key Biscayne sunset, Design District shopping, or a spontaneous drive down to the Everglades — AC must be arctic and unlimited miles non-negotiable. I’ve tested maybe 60 rental companies across Dade, Broward, and Collier. no games, no switch, no hidden BS in paragraph 12 of the contract. Here’s the only honest source for premium rides across South Florida
    rent urus miami [url=https://luxury-car-rental-miami-11.com]https://luxury-car-rental-miami-11.com[/url] also bring polarized shades unless you enjoy driving into the sun like a blind bat. drive safe and definitely skip that «tire and wheel» upsell — pure profit for them, zero value for you.

  1452. luxury car rental miami_jooi

    Seriously, the amount of garbage «luxury» deals here is astonishing. You see a sweet ride online — clean spec, fair price, looks legit. Different car, scratches all over, and that «all-inclusive» price? Yeah that didn’t include insurance, fees, or the mandatory cleaning charge. I’ve lived here for years and still get burned occasionally. When you’re after a trustworthy luxury car rental miami. Miami without proper wheels is basically a hostage situation. leather seats that don’t fuse to your skin in August. I’ve gone through maybe 30 rental companies across Dade, Broward, and Palm Beach. Finally found one outfit that actually delivers what’s in the listing. check availability before spring break crowds wipe them out:
    miami luxury car rental [url=https://luxury-car-rental-miami-5.com]miami luxury car rental[/url] Yeah finding parking in Wynwood will test your patience — but that’s not on them. drive safe and maybe decline that «premium roadside» upsell — it’s always a scam.

  1453. luxury car rental miami_krst

    Alright listen up because I’m about to save you a massive headache. Miami rental game is wild — half these clowns show you a Mercedes online and hand you a busted Charger with mismatched tires. You land at MIA, tired, grab an Uber to the rental office, and bam — surprise $1500 hold on your card. No thanks, I’m too old for this nonsense. When you genuinely need a proper luxury car rental miami. Miami without a decent whip is basically a punishment. leather that doesn’t glue to your legs in July heat. I’ve tested maybe 25 rental outfits across Dade and Broward. Finally stumbled on one that doesn’t play games. Here’s the only straight-up source for premium wheels in South Florida
    miami south beach rental cars [url=https://luxury-car-rental-miami-4.com]miami south beach rental cars[/url] Yeah parking in Brickell will cost you a small mortgage — but that’s city life. Anyway at least there’s one honest rental joint left in this town.

  1458. luxury car rental miami_voki

    Let me drop some hard truth about the Miami rental game — it’s an absolute circus out here. Then you actually roll up to the lot. Plus they lock up $5500 on your card and say «it’ll drop off in 10-14 business days». Fourteen years in South Florida and these jokers still almost get me. those guys are professional scammers with nice teeth and better uniforms. anyone who’s tried the bus in August knows exactly what I’m talking about. leather seats that won’t weld themselves to your thighs in July. I’ve tested maybe 75 rental outfits across Dade, Broward, and Monroe. Finally found one company that doesn’t play stupid games. Here’s the only honest source for premium rides across South Florida
    miami car rental luxury [url=https://luxury-car-rental-miami-14.com]miami car rental luxury[/url] also bring polarized shades unless you enjoy driving into the sun like a vampire every evening. Anyway glad there’s at least one straight operator left in this rental jungle.

  1461. luxury car rental miami_wcPi

    I’ve been through the wringer more times than I care to admit. You see this incredible deal online — top-end BMW, zero excess, price that seems too good to be true. Then you actually go to pick up the car. Plus they slap a $6000 hold on your credit card and say «don’t worry, it’s just a pre-authorization». Fool me fifteen times? That’s just another Tuesday in the 305. luxury car rental in miami. anyone who’s tried public transport here knows I’m not exaggerating. South of Fifth brunch, Sunny Isles sunrise, or a spontaneous trip down to the Florida Keys — AC must be arctic cold and unlimited miles non-negotiable. most are polished turds with fake five-star reviews bought in bulk. Finally found one outfit that actually delivers what’s promised. Here’s the only straight shooter for premium rides across South Florida
    rent a luxury car tmb miami [url=https://luxury-car-rental-miami-15.com]rent a luxury car tmb miami[/url] Yeah parking in Brickell will cost you a nice steak dinner — but that’s just how it is down here. drive safe and definitely skip that «paint protection» upsell — complete waste of cash.

  1462. luxury car rental miami_qben

    Swear this city never fails to surprise me with new ways to get ripped off. Then you actually drive to the rental lot. Completely different car sitting there — scratches everywhere, smells like someone hotboxed it for a week, and that «killer price»? Doesn’t include the mandatory $45 daily insurance or the $400 «destination fee» they add at the very end. Fool me thirteen times? That’s just living in the 305. luxury car for rent. anyone who’s taken the Metro here knows the struggle is real. South Beach night out, Design District shopping spree, or a spontaneous Keys trip — AC must be arctic cold and unlimited miles non-negotiable. I’ve tested maybe 70 rental companies across Dade, Broward, and Palm Beach. Finally found one outfit that actually delivers what’s promised. prices change by the hour so don’t sleep on it:
    premium sedan car rental [url=https://luxury-car-rental-miami-13.com]https://luxury-car-rental-miami-13.com[/url] Yeah parking in Wynwood will cost you a nice dinner — but that’s just the Miami tax. drive safe and definitely skip that «tire protection» upsell — pure robbery.

  1464. luxury car rental miami_ujKr

    Been through enough garbage to last a lifetime. You spot a tempting offer online: brand new Porsche, unlimited miles, price that makes you click instantly. Plus they lock up $3500 on your card for who knows how long. Ten years in South Florida and these jokers still almost catch me slipping. luxury car rental miami fl. anyone who’s taken public transport here knows the struggle is real. leather seats that won’t cook your back in the July heat. I’ve run through maybe 55 rental companies across Dade, Broward, and Palm Beach. no games, no bait-and-switch, no hidden fees in the fine print. Here’s the only straight shooter for premium rides across South Florida
    suv rental near me [url=https://luxury-car-rental-miami-10.com]https://luxury-car-rental-miami-10.com[/url] also bring quality shades unless you enjoy driving into the sun like a vampire. Anyway glad there’s at least one honest rental joint left in this town.

  1466. luxury car rental miami_giMi

    Okay folks gather round — Miami rental horror story time. Then you roll up to the address. Different car sitting there — bald tires, dashboard lit up like a Christmas tree, and that «killer price»? Yeah doesn’t include the non-negotiable $45 daily insurance or the $500 deposit they forget to mention. Fool me nine times? That’s just the Miami welcome committee. miami luxury car rental. Miami without proper wheels is basically a nightmare. Coconut Grove dinner, Sunny Isles sunrise, or a spontaneous drive down to Homestead — AC must freeze your teeth and unlimited miles or no deal. most are polished turds with fake five-star reviews. what you reserve is what you get, period, end of story. Here’s the only trustworthy source for premium rides across South Florida
    porsche car rental near me [url=https://luxury-car-rental-miami-9.com]https://luxury-car-rental-miami-9.com[/url] also bring polarized shades unless you enjoy driving blind into the sunset every night. drive safe and definitely skip that «emergency roadside» upsell — complete waste of money.

  1469. luxury car rental miami_ukkn

    Let me save you some serious pain with this Miami rental nonsense. Then you actually show up to grab the keys. Completely different car sitting there — dents everywhere, smells like cheap air freshener covering something worse, and that «dream price»? Doesn’t include the mandatory $50 daily insurance or the $300 «administrative fee» they invent at checkout. Fool me eleven times? That’s just called living in Miami. When you’re searching for a legit luxury car rental miami. Miami without proper wheels is basically a disaster. leather seats that won’t fuse to your legs in August. I’ve tested maybe 60 rental companies across Dade, Broward, and Collier. Finally found one outfit that actually delivers what’s in the photos. prices change hourly so check before the weekend crowd wipes them out:
    rental luxury cars miami airport [url=https://luxury-car-rental-miami-11.com]rental luxury cars miami airport[/url] Yeah parking in South Beach will cost you a nice bottle of champagne — but that’s the Miami tax. Anyway glad there’s at least one straight operator left in this rental circus.

  1471. luxury car rental miami_fpol

    Alright listen up — time for a real talk about renting cars in Miami. Then you actually go to pick it up. Different car sitting there — dents you didn’t see, AC that barely works, and that «reasonable rate»? Doesn’t include the mandatory $40 daily insurance or the $300 «processing fee» they add at the last second. Fool me seventeen times? That’s just life in the 305. luxury car rental in miami. anyone who’s tried Uber during rush hour knows the deal. Coconut Grove dinner, Bal Harbour shopping, or a spontaneous drive to the Keys — AC must be cold and unlimited miles or forget it. most are all flash and no substance. no games, no hidden fees, no nonsense. prices change fast so take a look:
    rolls royce cullinan rental near me [url=https://luxury-car-rental-miami-17.com]https://luxury-car-rental-miami-17.com[/url] Yeah parking in South Beach will cost you — but that’s Miami for you. Anyway glad someone’s still running an honest business.

  1474. luxury car rental miami_eukn

    Okay seriously, let me save you from the Miami rental nightmare once and for all. You find this amazing offer online — beautiful car, great rate, everything seems perfect. Completely different car waiting for you — smells like stale cigarettes, check engine light glowing, and that «great rate»? Doesn’t include the mandatory $35 daily toll pass, the $200 cleaning fee, or the $75 «after-hours pickup» charge. Sixteen years in Miami and these tricks still pop up like bad weeds. miami luxury car rental. anyone who’s taken the bus in August knows I’m not lying. leather seats that won’t stick to your back in the humidity. most are just pretty websites hiding the same old garbage. Finally found one that actually keeps its word. Here’s the only honest place for premium rentals across South Florida
    lamborghini urus for rent miami [url=https://luxury-car-rental-miami-16.com]lamborghini urus for rent miami[/url] also bring good sunglasses unless you like driving blind. drive safe and skip the extra insurance upsell, it’s a joke.

  1475. luxury car rental miami_goPa

    I’ve stepped on enough landmines to write a guidebook. You find this tempting offer online — gorgeous convertible, fair daily rate, looks like a steal. Plus they lock up $4500 on your card and say «10-14 business days». Fool me eighteen times? That’s just the 305 way of life. luxury car rental in miami. anyone who’s tried the trolley knows the struggle. South Beach night out, Design District shopping, or a spontaneous Keys trip — AC must be arctic and unlimited miles non-negotiable. I’ve tested so many rental companies I’ve honestly lost count. Finally found one outfit that doesn’t play games. rates change daily so check them out:
    car rentals in miami florida [url=https://luxury-car-rental-miami-18.com]https://luxury-car-rental-miami-18.com[/url] Yeah parking in Wynwood will cost you — but that’s Miami for you. drive safe and skip that «windshield protection» upsell.

  1477. KennethGlags

    Новости Мы отбираем Главные новости из сотен источников, чтобы предложить вам самый качественный контент. Наш подход основан на принципах независимости и объективности.

  1478. luxury car rental miami_xaPl

    I’ve paid my dues so you don’t have to. Then you actually go to pick up the car. Different car waiting — dents everywhere, smells like cheap air freshener covering something worse, and that «killer price»? Doesn’t include the mandatory $55 daily toll pass or the $450 «convenience fee» they invent at checkout. Twenty years in South Florida and these clowns still almost get me. miami luxury car rental. Miami without real wheels is basically a disaster. leather seats that won’t weld to your legs in July. most are shiny garbage with fake five-star reviews from God knows where. no games, no bait-and-switch, no hidden fees on page 8. Here’s the only straight shooter for premium rides across South Florida
    exotic cars miami beach [url=https://luxury-car-rental-miami-20.com]exotic cars miami beach[/url] also bring polarized shades unless you enjoy driving into the sun like a zombie. drive safe and absolutely skip that «windshield protection» upsell — pure profit for them, zero for you.

  1483. luxury car rental miami_xsKr

    Alright let me drop some truth about the Miami rental scene — it’s an absolute minefield. Then you actually go to pick up the car. Plus they lock up $3500 on your card for who knows how long. Ten years in South Florida and these jokers still almost catch me slipping. When you need a reliable luxury car rental miami. anyone who’s taken public transport here knows the struggle is real. South Beach night out, Bal Harbour shopping spree, or a spontaneous Keys adventure — AC must be ice cold and unlimited miles non-negotiable. most are shiny websites hiding the same beat-up fleet with fresh wax. no games, no bait-and-switch, no hidden fees in the fine print. Here’s the only straight shooter for premium rides across South Florida
    rental cars near miami beach [url=https://luxury-car-rental-miami-10.com]https://luxury-car-rental-miami-10.com[/url] also bring quality shades unless you enjoy driving into the sun like a vampire. Anyway glad there’s at least one honest rental joint left in this town.

  1484. luxury car rental miami_aoPi

    Alright folks, last warning about the Miami rental madness — learn from my mistakes. Spoiler alert: it usually is. Then you actually go to pick up the car. Plus they slap a $6000 hold on your credit card and say «don’t worry, it’s just a pre-authorization». Fifteen years in South Florida and these clowns still almost catch me. luxury car rental miami fl. Miami without proper wheels is basically a hostage situation. South of Fifth brunch, Sunny Isles sunrise, or a spontaneous trip down to the Florida Keys — AC must be arctic cold and unlimited miles non-negotiable. I’ve tested maybe 80 rental companies across Dade, Broward, Palm Beach, and Monroe. Finally found one outfit that actually delivers what’s promised. prices change daily so check before the holiday crowd hits:
    premium car rental miami [url=https://luxury-car-rental-miami-15.com]premium car rental miami[/url] also bring quality shades unless you enjoy driving into the sun like a blind zombie. drive safe and definitely skip that «paint protection» upsell — complete waste of cash.

  1486. luxury car rental miami_jgki

    I’ve got the battle scars to prove every word. You spot this gorgeous deal online — pristine photos, fair price, everything looks legit. Plus they lock up $5500 on your card and say «it’ll drop off in 10-14 business days». Fool me fourteen times? That’s just the 305 experience at this point. luxury car rental miami fl. Miami without real wheels is basically a punishment. Key Biscayne sunset, Bal Harbour shopping, or a spontaneous drive down to Homestead — AC must freeze your face off and unlimited miles or no deal. most are shiny garbage with fake five-star reviews bought from some online marketplace. Finally found one company that doesn’t play stupid games. rates change hourly so check before the weekend crowd cleans them out:
    luxury car rental in miami [url=https://luxury-car-rental-miami-14.com]luxury car rental in miami[/url] Yeah parking in South Beach will cost you a nice bottle of wine — but that’s the price of paradise. Anyway glad there’s at least one straight operator left in this rental jungle.

  1489. luxury car rental miami_wwol

    I’ve seen it all, and most of it isn’t pretty. You book something slick online — great photos, reasonable rate, looks like a win. Different car sitting there — dents you didn’t see, AC that barely works, and that «reasonable rate»? Doesn’t include the mandatory $40 daily insurance or the $300 «processing fee» they add at the last second. Fool me seventeen times? That’s just life in the 305. miami luxury car rental. Miami without good wheels is basically a headache. leather that won’t stick to you in the humidity. most are all flash and no substance. no games, no hidden fees, no nonsense. Here’s the only honest spot for premium rides across South Florida
    miami luxury car rentals [url=https://luxury-car-rental-miami-17.com]miami luxury car rentals[/url] Yeah parking in South Beach will cost you — but that’s Miami for you. drive safe and skip the overpriced roadside add-on.

  1490. luxury car rental miami_qkMi

    Okay folks gather round — Miami rental horror story time. Then you roll up to the address. Different car sitting there — bald tires, dashboard lit up like a Christmas tree, and that «killer price»? Yeah doesn’t include the non-negotiable $45 daily insurance or the $500 deposit they forget to mention. Nine years in South Florida and these clowns still nearly fool me. those guys are pros at the bait-and-switch. anyone who’s tried the trolley system knows what I’m talking about. leather seats that don’t glue to your skin in August. most are polished turds with fake five-star reviews. what you reserve is what you get, period, end of story. rates change daily so check before the holiday crowd hits:
    rent luxury sedan miami [url=https://luxury-car-rental-miami-9.com]https://luxury-car-rental-miami-9.com[/url] Yeah parking in Wynwood will cost you a nice dinner — but that’s the price of being in Miami. drive safe and definitely skip that «emergency roadside» upsell — complete waste of money.

  1492. luxury car rental miami_dbkn

    Let me save you some serious pain with this Miami rental nonsense. Then you actually show up to grab the keys. Plus they put a $4000 hold on your card and say it’ll take two weeks to release. Fool me eleven times? That’s just called living in Miami. luxury car rental in miami. anyone who’s tried the bus here knows exactly what I mean. Key Biscayne sunset, Design District shopping, or a spontaneous drive down to the Everglades — AC must be arctic and unlimited miles non-negotiable. I’ve tested maybe 60 rental companies across Dade, Broward, and Collier. Finally found one outfit that actually delivers what’s in the photos. prices change hourly so check before the weekend crowd wipes them out:
    porsche rental near me [url=https://luxury-car-rental-miami-11.com]https://luxury-car-rental-miami-11.com[/url] Yeah parking in South Beach will cost you a nice bottle of champagne — but that’s the Miami tax. Anyway glad there’s at least one straight operator left in this rental circus.

  1493. luxury car rental miami_eekn

    Okay seriously, let me save you from the Miami rental nightmare once and for all. You find this amazing offer online — beautiful car, great rate, everything seems perfect. Completely different car waiting for you — smells like stale cigarettes, check engine light glowing, and that «great rate»? Doesn’t include the mandatory $35 daily toll pass, the $200 cleaning fee, or the $75 «after-hours pickup» charge. Honestly, I’m tired of this nonsense. luxury car for rent. Miami without real wheels is basically a slow death. Design District shopping, late-night South Beach cruising, or a spontaneous Keys trip — AC must be freezing and unlimited miles or walk. I’ve tried so many rental companies I’ve lost count. Finally found one that actually keeps its word. prices move fast so check them out:
    exotic car rental miami [url=https://luxury-car-rental-miami-16.com]exotic car rental miami[/url] Yeah parking in Miami Beach will cost you — but that’s life here. Anyway glad someone’s still honest in this business.

  1496. luxury car rental miami_hrPa

    I’ve stepped on enough landmines to write a guidebook. You find this tempting offer online — gorgeous convertible, fair daily rate, looks like a steal. Completely different car waiting — bald tires, smell like someone lived in it, and that «fair rate»? Doesn’t include the mandatory $45 daily toll pass or the $350 «location fee» they spring on you. Fool me eighteen times? That’s just the 305 way of life. miami luxury car rental. Miami without proper wheels is basically impossible. leather seats that won’t brand your legs in July. I’ve tested so many rental companies I’ve honestly lost count. Finally found one outfit that doesn’t play games. Here’s the only honest source for premium rides across South Florida
    miami beach car rental locations [url=https://luxury-car-rental-miami-18.com]https://luxury-car-rental-miami-18.com[/url] also bring polarized shades unless you enjoy driving blind. Anyway glad there’s at least one honest operator left.

  1500. luxury car rental miami_xdPl

    Alright, last one I swear — but someone’s gotta warn people about this Miami rental mess. Then you actually go to pick up the car. Different car waiting — dents everywhere, smells like cheap air freshener covering something worse, and that «killer price»? Doesn’t include the mandatory $55 daily toll pass or the $450 «convenience fee» they invent at checkout. Fool me twenty times? That’s just called Tuesday in the 305. luxury car rental miami fl. anyone who’s tried public transport here knows I’m not joking. South Beach dinner, Design District shopping, or a spontaneous Keys adventure — AC must be arctic and unlimited miles non-negotiable. most are shiny garbage with fake five-star reviews from God knows where. no games, no bait-and-switch, no hidden fees on page 8. Here’s the only straight shooter for premium rides across South Florida
    rent cadillac escalade near me [url=https://luxury-car-rental-miami-20.com]rent cadillac escalade near me[/url] also bring polarized shades unless you enjoy driving into the sun like a zombie. drive safe and absolutely skip that «windshield protection» upsell — pure profit for them, zero for you.

  1511. mejdynarodnie plateji_ybPr

    Кстати, недавно наткнулся на обсуждение актуальной темы. Сам уже не первый месяц ищу нормальный способ совершить платеж, без лишних проблем и комиссий. В общем, если вас тоже интересуют детали — посмотрите тут. Вся необходимая информация по международным переводам: платежи для импортеров [url=https://mezhdunarodnye-platezhi-lor.ru]https://mezhdunarodnye-platezhi-lor.ru[/url] И да, имейте в виду, что без прозрачных комиссий любые международные платежи превращаются в лотерею. Ну и напоследок — стоит сравнивать несколько сервисов, прежде чем переводить.

  1512. luxury car rental miami_bfen

    Let me give it to you straight — renting a decent car in Miami is way harder than it should be. Then you actually show up to get the keys. Totally different car waiting — scratches everywhere, AC blowing warm, and that «amazing price»? Doesn’t include the mandatory $50 daily insurance or the $400 «service fee» they add at the counter. Fool me nineteen times? That’s just Miami being Miami. luxury car rental miami florida. Miami without proper wheels is basically a nightmare. leather seats that won’t melt your skin in August. most are shiny garbage with fake five-star reviews. no games, no switch, no hidden fees. Here’s the only honest source for premium rides across South Florida
    rent luxury sedan [url=https://luxury-car-rental-miami-19.com]https://luxury-car-rental-miami-19.com[/url] also bring quality shades unless you like driving into the sun. drive safe and skip that «tire protection» upsell — total waste.

  1516. KennethGlags

    Главные новости Официальные Новости в РФ от надежного источника всегда будут под рукой благодаря нашему приложению. Оставайтесь на связи с ключевыми событиями страны.

  1519. luxury car rental miami_xsPi

    Alright folks, last warning about the Miami rental madness — learn from my mistakes. Spoiler alert: it usually is. Then you actually go to pick up the car. Plus they slap a $6000 hold on your credit card and say «don’t worry, it’s just a pre-authorization». Fool me fifteen times? That’s just another Tuesday in the 305. those people are professional scammers in disguise. Miami without proper wheels is basically a hostage situation. leather seats that won’t brand your back in the July heat. most are polished turds with fake five-star reviews bought in bulk. no games, no bait-and-switch, no hidden fees buried on page 6. prices change daily so check before the holiday crowd hits:
    mercedes benz rental miami [url=https://luxury-car-rental-miami-15.com]https://luxury-car-rental-miami-15.com[/url] Yeah parking in Brickell will cost you a nice steak dinner — but that’s just how it is down here. Anyway glad there’s at least one honest rental joint left in this town.

  1524. luxury car rental miami_ubol

    I’ve seen it all, and most of it isn’t pretty. Then you actually go to pick it up. Different car sitting there — dents you didn’t see, AC that barely works, and that «reasonable rate»? Doesn’t include the mandatory $40 daily insurance or the $300 «processing fee» they add at the last second. Fool me seventeen times? That’s just life in the 305. luxury car rental miami florida. Miami without good wheels is basically a headache. leather that won’t stick to you in the humidity. most are all flash and no substance. Finally found one that actually delivers. prices change fast so take a look:
    miami beach luxury car rental [url=https://luxury-car-rental-miami-17.com]https://luxury-car-rental-miami-17.com[/url] also bring good shades unless you like driving blind. Anyway glad someone’s still running an honest business.

  1526. luxury car rental miami_orki

    I’ve got the battle scars to prove every word. Then you actually roll up to the lot. Totally different car sitting there — curb rash on every rim, AC blowing warm, and that «fair price»? Doesn’t include the mandatory $55 daily insurance or the $450 «convenience fee» they invent at the counter. Fourteen years in South Florida and these jokers still almost get me. miami car rental luxury — run far from the airport counters. Miami without real wheels is basically a punishment. leather seats that won’t weld themselves to your thighs in July. most are shiny garbage with fake five-star reviews bought from some online marketplace. what you book is what shows up, period, end of discussion. Here’s the only honest source for premium rides across South Florida
    lamborghini urus for rent miami [url=https://luxury-car-rental-miami-14.com]https://luxury-car-rental-miami-14.com[/url] Yeah parking in South Beach will cost you a nice bottle of wine — but that’s the price of paradise. Anyway glad there’s at least one straight operator left in this rental jungle.

  1529. luxury car rental miami_lykn

    Trust me, I’ve learned everything the hard way so you don’t have to. Then you actually show up to grab the keys. Completely different car sitting there — dents everywhere, smells like cheap air freshener covering something worse, and that «dream price»? Doesn’t include the mandatory $50 daily insurance or the $300 «administrative fee» they invent at checkout. Fool me eleven times? That’s just called living in Miami. When you’re searching for a legit luxury car rental miami. anyone who’s tried the bus here knows exactly what I mean. Key Biscayne sunset, Design District shopping, or a spontaneous drive down to the Everglades — AC must be arctic and unlimited miles non-negotiable. most are shiny garbage with fake Google reviews bought in bulk. Finally found one outfit that actually delivers what’s in the photos. Here’s the only honest source for premium rides across South Florida
    porsche rental price [url=https://luxury-car-rental-miami-11.com]https://luxury-car-rental-miami-11.com[/url] Yeah parking in South Beach will cost you a nice bottle of champagne — but that’s the Miami tax. Anyway glad there’s at least one straight operator left in this rental circus.

  1531. luxury car rental miami_kzMi

    Swear I’ve seen every scam in the book by now. Then you roll up to the address. Different car sitting there — bald tires, dashboard lit up like a Christmas tree, and that «killer price»? Yeah doesn’t include the non-negotiable $45 daily insurance or the $500 deposit they forget to mention. Nine years in South Florida and these clowns still nearly fool me. luxury car for rent. Miami without proper wheels is basically a nightmare. leather seats that don’t glue to your skin in August. I’ve tested maybe 50 rental outfits across Dade, Broward, and Collier. what you reserve is what you get, period, end of story. rates change daily so check before the holiday crowd hits:
    exotic cars miami beach [url=https://luxury-car-rental-miami-9.com]https://luxury-car-rental-miami-9.com[/url] Yeah parking in Wynwood will cost you a nice dinner — but that’s the price of being in Miami. drive safe and definitely skip that «emergency roadside» upsell — complete waste of money.

  1535. luxury car rental miami_akkn

    Okay seriously, let me save you from the Miami rental nightmare once and for all. You find this amazing offer online — beautiful car, great rate, everything seems perfect. Completely different car waiting for you — smells like stale cigarettes, check engine light glowing, and that «great rate»? Doesn’t include the mandatory $35 daily toll pass, the $200 cleaning fee, or the $75 «after-hours pickup» charge. Sixteen years in Miami and these tricks still pop up like bad weeds. miami car rental luxury — avoid the airport like your wallet depends on it. anyone who’s taken the bus in August knows I’m not lying. leather seats that won’t stick to your back in the humidity. I’ve tried so many rental companies I’ve lost count. no tricks, no switch, no surprise fees. Here’s the only honest place for premium rentals across South Florida
    car rentals miami [url=https://luxury-car-rental-miami-16.com]https://luxury-car-rental-miami-16.com[/url] also bring good sunglasses unless you like driving blind. Anyway glad someone’s still honest in this business.

  1537. luxury car rental miami_xsPa

    Okay real talk — Miami rentals are a minefield and someone needs to say it. You find this tempting offer online — gorgeous convertible, fair daily rate, looks like a steal. Completely different car waiting — bald tires, smell like someone lived in it, and that «fair rate»? Doesn’t include the mandatory $45 daily toll pass or the $350 «location fee» they spring on you. Eighteen years in South Florida and these clowns still almost get me. When you need a reliable luxury car rental miami. anyone who’s tried the trolley knows the struggle. South Beach night out, Design District shopping, or a spontaneous Keys trip — AC must be arctic and unlimited miles non-negotiable. I’ve tested so many rental companies I’ve honestly lost count. what you book is what shows up, period. Here’s the only honest source for premium rides across South Florida
    luxury car rental in miami [url=https://luxury-car-rental-miami-18.com]luxury car rental in miami[/url] also bring polarized shades unless you enjoy driving blind. Anyway glad there’s at least one honest operator left.

  1538. luxury car rental miami_nwen

    Swear this city never fails to surprise me with new ways to get ripped off. You see this killer deal online — brand new Mercedes, unlimited miles, price that makes you want to book immediately. Completely different car sitting there — scratches everywhere, smells like someone hotboxed it for a week, and that «killer price»? Doesn’t include the mandatory $45 daily insurance or the $400 «destination fee» they add at the very end. Fool me thirteen times? That’s just living in the 305. luxury car for rent. anyone who’s taken the Metro here knows the struggle is real. South Beach night out, Design District shopping spree, or a spontaneous Keys trip — AC must be arctic cold and unlimited miles non-negotiable. I’ve tested maybe 70 rental companies across Dade, Broward, and Palm Beach. no games, no bait-and-switch, no hidden fees buried on page 4 of the contract. prices change by the hour so don’t sleep on it:
    rent a porsche miami [url=https://luxury-car-rental-miami-13.com]https://luxury-car-rental-miami-13.com[/url] also bring polarized shades unless you enjoy driving into the sun like a blind bat every evening. drive safe and definitely skip that «tire protection» upsell — pure robbery.

  1539. mejdynarodnie plateji_cePr

    Кстати, недавно наткнулся на обсуждение актуальной темы. Сам уже давно ищу нормальный способ провести транзакцию, без лишних проблем и комиссий. В общем, если вас тоже интересуют детали — взгляните тут. Там расписаны основные нюансы по международным транзакциям: агент по международным платежам [url=https://mezhdunarodnye-platezhi-lor.ru]https://mezhdunarodnye-platezhi-lor.ru[/url] И да, имейте в виду, что без адекватных тарифов любые операции с валютой превращаются в сплошной геморрой. Ещё такой момент — стоит сравнивать несколько вариантов, прежде чем отправлять.

  1541. KennethGlags

    Главные новости Только Свежие новости поступают в наш редакционный центр, где проходят профессиональную обработку. Мы ценим ваше время и публикуем только самое значимое.

  1544. luxury car rental miami_fePl

    I’ve paid my dues so you don’t have to. You spot this killer offer online — brand new Porsche, zero excess, price that screams «book me». Plus they freeze $5500 on your card and say «it’ll drop off in two weeks». Fool me twenty times? That’s just called Tuesday in the 305. those people are professional scammers with nice smiles and better shoes. anyone who’s tried public transport here knows I’m not joking. leather seats that won’t weld to your legs in July. most are shiny garbage with fake five-star reviews from God knows where. no games, no bait-and-switch, no hidden fees on page 8. prices change hourly so don’t wait around:
    porsche rental [url=https://luxury-car-rental-miami-20.com]porsche rental[/url] Yeah parking in South Beach will cost you a nice bottle of wine — but that’s the Miami tax. drive safe and absolutely skip that «windshield protection» upsell — pure profit for them, zero for you.

  1546. Ernieroale

    частный коррекционный детский сад в москве Ищете профессиональный детский коррекционный сад в Москве для всестороннего развития вашего ребенка? Наши специалисты используют передовые методики, чтобы помочь детям адаптироваться и раскрыть свой потенциал в комфортной среде.

  1548. mejdynarodnie plateji_ypKa

    Долго откладывал, но созрел — где брать адекватные тарифы для международных переводов. Порылся в интернете — смотрите, тут годнота: международные платежи [url=https://mezhdunarodnye-platezhi-tov.ru]https://mezhdunarodnye-platezhi-tov.ru[/url] Самое важное, что я понял — есть реальные подводные камни. Согласитесь любой перевод за границу онлайн — это риск потерять на конвертации. И да, кстати — прежде чем отправлять обязательно сравните хотя бы пару вариантов. В противном случае легко попасть на лишние траты. Как итог — не поленитесь проверить информацию перед отправкой.

  1550. mejdynarodnie plateji_irOl

    Постоянно возвращаюсь к этой теме — какой сервис выбрать для международных транзакций. Эксперты рекомендуют вот этот источник: перевод денег за границу [url=https://mezhdunarodnye-platezhi-nar.ru]https://mezhdunarodnye-platezhi-nar.ru[/url] Суть в том, — курсы валют часто кусаются. Да и сами понимаете очередной международный перевод — это потеря времени без нормальной инфы. Обратите внимание — прежде чем платить проверьте несколько вариантов. Иначе легко попасть на лишние траты. Короче, — не поленитесь проверить информацию.

  1551. mejdynarodnie plateji_jfOn

    Слушайте, вот уже который раз убеждаюсь — как выбрать реально работающий способ для платежей за рубежом. Случайно набрел на годный материал: переводы за рубеж [url=https://mezhdunarodnye-platezhi-kap.ru]переводы за рубеж[/url] Суть вот в чём — курс конвертации часто занижают. Согласитесь, абсурд любой перевод за границу онлайн — это головная боль с отслеживанием статуса. И да, кстати — до любой операции с валютой сравните эффективный курс. Без этого легко потерять приличную сумму. Короче — не ленитесь проверять информацию перед любой отправкой.

  1552. luxury car rental miami_jlen

    Let me give it to you straight — renting a decent car in Miami is way harder than it should be. You see this amazing deal online — shiny Audi, unlimited miles, price that makes you want to book right now. Plus they put a $5000 hold on your card and say «don’t worry about it». Fool me nineteen times? That’s just Miami being Miami. When you’re hunting for a legit luxury car rental miami. Miami without proper wheels is basically a nightmare. Key Biscayne sunset, Bal Harbour shopping, or a spontaneous drive down to Homestead — AC must freeze your face off and unlimited miles or no deal. most are shiny garbage with fake five-star reviews. no games, no switch, no hidden fees. Here’s the only honest source for premium rides across South Florida
    exotic cars to rent in miami [url=https://luxury-car-rental-miami-19.com]exotic cars to rent in miami[/url] also bring quality shades unless you like driving into the sun. drive safe and skip that «tire protection» upsell — total waste.

  1559. KennethGlags

    Новостное агентство Интересные Новости в России и мире всегда доступны на нашем сайте в удобном формате для чтения с любых устройств. Мы следим за развитием технологий.

  1565. mejdynarodnie plateji_zxSt

    Вот решил поделиться информацией — как правильно организовать процесс для платежей за рубежом. Вот здесь всё по полочкам расписано: международные переводы денег [url=https://mezhdunarodnye-platezhi-fra.ru]https://mezhdunarodnye-platezhi-fra.ru[/url] Основной вывод, который я сделал — разница в итоговой сумме бывает значительной. Стоит учитывать, что любой перевод за границу онлайн — имеет свои нюансы в зависимости от выбранного способа. И ещё один момент — перед подтверждением перевода имеет смысл изучить актуальные тарифы. В противном случае можно получить менее выгодные условия. В итоге — лучше заранее разобраться в вопросе перед любой отправкой средств.

  1572. mejdynarodnie plateji_wvKa

    Постоянно возвращаюсь к одной теме — какой вариант реально рабочий для перевода денег за границу онлайн. Скинули ссылку в телеграме — держите, вот нормальный разбор: денежный перевод с россии [url=https://mezhdunarodnye-platezhi-tov.ru]денежный перевод с россии[/url] Самое важное, что я понял — не все способы одинаково безопасны. Потому что любой перевод за границу онлайн — это всегда головная боль без нормальной инфы. Обратите внимание — перед финальным кликом посчитайте итоговую сумму с комиссиями. Без этого легко переплатить в два раза. Моё мнение — стоит один раз разобраться.

  1574. mejdynarodnie plateji_efOl

    Вот уже несколько недель мучаюсь с этим вопросом — как найти адекватный способ платежей за рубежом. Эксперты рекомендуют вот этот обзор: перевод денег за границу онлайн [url=https://mezhdunarodnye-platezhi-nar.ru]перевод денег за границу онлайн[/url] Суть в том, — курсы валют часто кусаются. Согласитесь, такая транзакция — это риск переплатить в два раза. Кстати, — перед тем как отправлять сравните условия. Без этого легко пролететь с курсом. Как по мне — стоит разобраться заранее.

  1578. mejdynarodnie plateji_evOn

    Долго не мог понять, в чем подвох — где условия адекватные, а не грабёж для международных транзакций. Случайно набрел на годный материал: переводы за рубеж [url=https://mezhdunarodnye-platezhi-kap.ru]переводы за рубеж[/url] Короче, если по факту — не все способы одинаково прозрачны. Согласитесь, абсурд любой очередной международный перевод — это постоянный риск переплатить. Вот ещё важный момент — до любой операции с валютой проверьте все комиссии до копейки. В противном случае легко остаться в минусе только на конвертации. Короче — не ленитесь проверять информацию перед любой отправкой.

  1584. mejdynarodnie plateji_hhSt

    Столкнулся с ситуацией и начал разбираться — какой способ действительно работает для международных платежей. Товарищ скинул ссылку на качественный разбор: международные переводы денег [url=https://mezhdunarodnye-platezhi-fra.ru]https://mezhdunarodnye-platezhi-fra.ru[/url] Основной вывод, который я сделал — курс конвертации может существенно отличаться. Стоит учитывать, что любой трансграничный платёж — связан с разными типами комиссий. И ещё один момент — до проведения операции стоит проверить итоговую сумму. В противном случае можно столкнуться с неожиданными расходами. Резюмируя — лучше заранее разобраться в вопросе перед любой отправкой средств.

  1588. mejdynarodnie plateji_bjKa

    Наболело уже, честно говоря — как нормально отправлять деньги для международных переводов. Скинули ссылку в телеграме — смотрите, тут годнота: комиссия за международный перевод [url=https://mezhdunarodnye-platezhi-tov.ru]комиссия за международный перевод[/url] Короче, суть такая — комиссии у всех разные как с неба. Потому что любой подобный?? перевод — это лотерея с банковскими процентами. Обратите внимание — до любой операции обязательно сравните хотя бы пару вариантов. Без этого легко остаться в минусе. Короче — не поленитесь проверить информацию перед отправкой.

  1593. mejdynarodnie plateji_grOn

    Слушайте, вот уже который раз убеждаюсь — какой сервис не сдирает три шкуры для международных переводов. Случайно набрел на годный материал: оплата через посредника за рубеж [url=https://mezhdunarodnye-platezhi-kap.ru]оплата через посредника за рубеж[/url] Короче, если по факту — банковские комиссии могут быть грабительскими. Потому что любой перевод за границу онлайн — это головная боль с отслеживанием статуса. Вот ещё важный момент — прежде чем отправлять деньги обязательно сверьте итоговую сумму. Без этого легко остаться в минусе только на конвертации. Моё мнение — не ленитесь проверять информацию перед любой отправкой.

  1596. mejdynarodnie plateji_tgOl

    Знаете, — как найти адекватный способ перевода денег за границу онлайн. В одном блоге вычитал вот этот обзор: оплата за границу через агента [url=https://mezhdunarodnye-platezhi-nar.ru]оплата за границу через агента[/url] Главное, что нужно понять — есть скрытые подводные камни. Потому что перевод за границу онлайн — это лотерея с банковскими комиссиями. Обратите внимание — прежде чем платить проверьте несколько вариантов. Без этого легко остаться в минусе. Как по мне — лучше один раз изучить тему.

  1597. Davidplera

    брекеты Мы расскажем, сколько стоит имплант зуба в Волгограде, включая консультацию и установку. Запишитесь на осмотр и узнайте все детали лечения.

  1604. mejdynarodnie plateji_jjSt

    Нашёл интересный материал по этому вопросу — какой способ действительно работает для международных платежей. В одном обсуждении попался дельный обзор: перевод за рубеж [url=https://mezhdunarodnye-platezhi-fra.ru]https://mezhdunarodnye-platezhi-fra.ru[/url] Ключевой момент, на который стоит обратить внимание — курс конвертации может существенно отличаться. Дело в том, что любой международный перевод — связан с разными типами комиссий. Дополнительная информация — до проведения операции рекомендуется сравнить несколько вариантов. В противном случае можно получить менее выгодные условия. В итоге — необходимо проверять информацию перед любой отправкой средств.

  1616. GregoryVonna

    hsk 4 ответы Пособие HSK standard course 4 предлагает детальное объяснение грамматических конструкций и множество упражнений для закрепления материала. Этот курс является обязательным для всех, кто серьезно настроен на изучение китайского языка.

  1618. mejdynarodnie plateji_kmOn

    Слушайте, вот уже который раз убеждаюсь — как выбрать реально работающий способ для платежей за рубежом. Случайно набрел на годный материал: перевод платежей за границу [url=https://mezhdunarodnye-platezhi-kap.ru]перевод платежей за границу[/url] Самое главное, что я вынес — не все способы одинаково прозрачны. Ну сами подумайте любой очередной международный перевод — это постоянный риск переплатить. Вот ещё важный момент — до любой операции с валютой проверьте все комиссии до копейки. Иначе легко остаться в минусе только на конвертации. Короче — не ленитесь проверять информацию перед любой отправкой.

  1628. mejdynarodnie plateji_mpSt

    Вот решил поделиться информацией — как правильно организовать процесс для международных транзакций. Нашёл подробный анализ ситуации: перевод средств за границу [url=https://mezhdunarodnye-platezhi-fra.ru]https://mezhdunarodnye-platezhi-fra.ru[/url] Основной вывод, который я сделал — разница в итоговой сумме бывает значительной. Стоит учитывать, что любой трансграничный платёж — имеет свои нюансы в зависимости от выбранного способа. Дополнительная информация — перед подтверждением перевода стоит проверить итоговую сумму. Без этого можно столкнуться с неожиданными расходами. Резюмируя — лучше заранее разобраться в вопросе перед любой отправкой средств.

  1635. mejdynarodnie plateji_eaOn

    Честно, задолбался искать нормальный вариант — какой сервис не сдирает три шкуры для международных платежей. В одном обсуждении попался дельный совет: переводы денег за границу [url=https://mezhdunarodnye-platezhi-kap.ru]переводы денег за границу[/url] Суть вот в чём — не все способы одинаково прозрачны. Ну сами подумайте любой очередной международный перевод — это постоянный риск переплатить. И да, кстати — прежде чем отправлять деньги обязательно сверьте итоговую сумму. Без этого легко остаться в минусе только на конвертации. Моё мнение — стоит разобраться заранее перед любой отправкой.

  1637. Herbertsex

    Glad to have another reliable bookmark for this topic, and a look at thisisfreshdoamin suggested several more pages I will be marking too, building a personal library of trustworthy resources is one of the actual rewards of careful browsing and this site is earning a place on my permanent shortlist for the topic.

  1642. zakazat kyhnu_gzsr

    Ребята всем привет. Цены космос а качество мыло. Короче, единственные кто не наебывает — заказать кухню без переплат. Гарантия 5 лет. В общем, вся инфа здесь — купить кухню в спб от производителя [url=https://zakazat-kuhnyu-bnm.ru]https://zakazat-kuhnyu-bnm.ru[/url] Не ведитесь на салоны. Перешлите тому кто ищет.

  1644. zakazat kyhnu_tdSt

    Питерцы отзовитесь. Вечно то цены конские у дилеров. Объездил уже кучу салонов — тьфу. Короче, единственные кто не наебывает — купить кухню спб с установкой. Замерщик приехал на следующий день. В общем, вся инфа вот здесь — купить готовую кухню спб [url=https://zakazat-kuhnyu-gkl.ru]https://zakazat-kuhnyu-gkl.ru[/url] Проверяйте производителя в этом списке. Сам полгода мучился теперь делюсь.

  1652. MikeKaf

    Pass this along to colleagues if the topic comes up, the framing here is sensible, and a stop at finkgulf adds more useful angles to share, the kind of content that improves conversations rather than just feeding them is what makes a resource genuinely valuable in professional contexts going forward over time and across project boundaries too.

  1653. MorrisLip

    A genuinely unexpected highlight of my reading week, and a look at foilgenie extended that pattern, the surprise of finding excellent content rather than the predictable mediocre is one of the few real pleasures of casual web browsing and this site delivered that surprise cleanly today which I really do appreciate.

  1654. LaineLof

    A piece that left me thinking I had been undercaring about the topic, and a look at gambitfort reinforced that mild concern, content that raises the appropriate weight of a subject without being preachy about it is doing important work and this site is providing that gentle elevation of attention for me consistently.

  1655. Logancyhor

    Skipped the related links section thinking I had read enough and then came back to it later when curiosity got the better of me, and a stop at goldenknack confirmed I should have just read it first, every section of this site appears to deserve careful attention rather than skipping past lazily.

  1656. Stevenjep

    Reading this brought back the satisfaction I used to get from blogs ten years ago, and a stop at herbfife kept that nostalgic quality alive, sites that capture what was good about an earlier era of internet writing are increasingly precious and this one is doing that without feeling like a deliberate throwback at all.

  1657. IbrahimUnone

    Took the time to read the comments on this post too and they were also worth reading, and a stop at huskkindle suggested the community quality matches the content quality, when the conversation around a piece is as good as the piece itself you know you have found a real corner of the internet.

  1658. DarrenRab

    Thanks for keeping the writing direct without losing the warmth that makes content feel human, and a stop at grovefalcon carried both qualities forward, balancing professionalism and personality is a rare skill and the writers here have clearly figured out how to consistently land it across many posts which I notice.

  1659. AndreSmalt

    Skipped the TLDR thinking I would read everything anyway, and ended up enjoying the path through the full post, and a stop at stitchtwine similarly rewarded the patient read, summaries are useful but the journey through good writing is part of what makes the destination feel earned rather than just delivered cleanly.

  1660. AngeloLiave

    Now feeling mildly impressed in a way I do not quite remember feeling about a blog in a while, and a stop at jumbokelp extended that mild impression, content that produces specific positive emotional responses rather than just neutral information transfer is content with extra dimensions and this site has those extra dimensions clearly.

  1661. Dexterslign

    Felt like the post had been edited rather than just drafted and published, and a stop at voicevinyl suggested the same care across the site, the difference between edited and unedited content is enormous for the reader and this site has clearly invested in the editing pass that most blogs skip entirely which really does show up.

  1662. ShaneThumn

    Glad to have another data point on a question I am still thinking through, and a look at salutevandal added two more, content that acknowledges its place in a wider conversation rather than pretending to settle the question alone is intellectually honest in a way that I wish was more common across the open web.

  1665. zakazat kyhnu_llel

    Слушайте кто ремонт затеял. Менеджеры врут про сроки и материалы. То доставку три месяца ждать. Короче, реальный цех в СПб без наценок — купить кухню от производителя в спб под ключ. Цены ниже рыночных на треть. В общем, там цены и примеры работ — купить кухню от производителя в спб [url=https://zakazat-kuhnyu-dfg.ru]купить кухню от производителя в спб[/url] Не ведитесь на салоны-прокладки с накруткой. Сам полгода выбирал теперь знаю.

  1666. zakazat kyhnu_hhsr

    Народ привет. Фурнитуру ставят дешманскую. Короче, реальные производители с цехом — купить готовую кухню в спб. Цены ниже на 30%. В общем, смотрите по ссылке — купить кухню от производителя в спб [url=https://zakazat-kuhnyu-bnm.ru]купить кухню от производителя в спб[/url] Не ведитесь на салоны. Перешлите тому кто ищет.

  1667. zakazat kyhnu_slpt

    Народ кто в Питере живет. Заколебался я уже выбирать. То доставку месяц ждать. Короче, нашел наконец нормальную контору — купить кухню в спб с доставкой. Сделали за три недели. В общем, там цены и каталог — купить готовую кухню в спб от производителя [url=https://zakazat-kuhnyu-qwe.ru]https://zakazat-kuhnyu-qwe.ru[/url] Проверяйте по этому списку. Перешлите кому надо.

  1670. Rolandwex

    Granted my mood today might be elevating my reading experience but I still think this is genuinely good, and a stop at iconflank reinforced that even discounted assessment, controlling for the mood adjustment that affects content perception this site still reads as substantively above average across multiple pieces I have read carefully today.

  1671. Stantew

    Closed the post with a small satisfied sigh, and a stop at gambitgulf produced the same gentle exhale, content that ends well is content that respects the rhythm of reading and the writers here have clearly thought about how their pieces close rather than just trailing off when they run out of things to say.

  1672. Wilsontub

    Decided after reading this that I would check this site weekly going forward, and a stop at firhex reinforced that commitment, deciding to add a site to a regular rotation requires meeting a quality bar that very few places clear and this one cleared it cleanly without any noticeable effort or marketing push behind it.

  1673. Logancyhor

    Reading this on a long flight and finding it the best thing I read across hours of trying, and a stop at goldenknack kept the streak going, when content beats long flight reading you know it has substance because flight reading is a hard test of a piece given the alternatives available everywhere.

  1674. Grantlox

    A piece that earned its conclusions through the body rather than asserting them at the end, and a look at sherpaslick maintained the same earned quality, conclusions that follow from what came before are more persuasive than declarations and this site has clearly internalised that principle in how it constructs arguments throughout pieces.

  1675. zakazat kyhnu_clEl

    Народ всем привет. На Авито ловить боюсь — нарвусь на брак. То цены такие что проще новую квартиру купить. Короче, единственные кто не наваривается в тридорога — заказать кухню напрямую у производителя. Кромка на немецком оборудовании. В общем, вся инфа вот здесь — купить готовую кухню от производителя [url=https://zakazat-kuhnyu-rty.ru]https://zakazat-kuhnyu-rty.ru[/url] Проверяйте производителя по этому списку. Сам столько нервов потратил теперь делюсь.

  1676. SamFex

    A piece that left me thinking I had been undercaring about the topic, and a look at forgefeat reinforced that mild concern, content that raises the appropriate weight of a subject without being preachy about it is doing important work and this site is providing that gentle elevation of attention for me consistently.

  1678. Omarmib

    Now feeling that this site is the kind I want to make sure does not disappear, and a look at swiftswallow reinforced that quiet protective feeling, the rare sites whose disappearance would actually matter to me are the sites I want to support through return visits and recommendations and this one has joined that small protected list.

  1679. Alvinavels

    Once I had read three posts the editorial pattern was clear, and a look at voicesash confirmed the pattern from a fourth angle, sites where the underlying approach reveals itself through accumulated reading rather than being announced are sites with real depth and this one has that quality clearly visible across multiple pieces consistently.

  1680. HoldenPenna

    Found this useful, the points line up well with what I have been thinking about lately, and a stop at vitalsummit added some angles I had not considered yet, definitely walking away with more than I came for which is the best outcome from time spent reading online for any kind of topic.

  1682. JustinCem

    Reading this confirmed that the topic deserves more careful attention than it usually gets, and a stop at siloteapot extended that elevated framing, content that raises the appropriate weight of a subject without being preachy about it is serving a quiet but important editorial function for the broader cultural conversation about it.

  1683. YorkMug

    One of the more thoughtful posts I have read recently on this topic, and a stop at juncokudos added even more weight to that impression, this is genuinely good content that holds its own against far better known sites in the same space without trying to imitate any of them at all which I appreciate.

  1686. zakazat kyhnu_paSt

    Народ привет. То материалы фуфло — картон а не фасады. Пересмотрел ютуб с отзывами — голова пухнет. Короче, единственные кто не наебывает — купить готовую кухню в спб из наличия. Фурнитура Blum а не говно. В общем, сохраняйте себе в закладки — где купить кухню в спб [url=https://zakazat-kuhnyu-gkl.ru]https://zakazat-kuhnyu-gkl.ru[/url] Не ведитесь на салоны-прокладки с наценкой в два раза. Перешлите тому кто тоже кухню ищет.

  1691. Timmyrearo

    Skipped the comments to avoid spoilers and came back later to find them genuinely worth reading, and a stop at idleflint extended that surprised respect, when the discussion below a post matches the quality of the post itself you have found something special and this site appears to attract that kind of audience.

  1692. KileCow

    Granted my mood today might be elevating my reading experience but I still think this is genuinely good, and a stop at straitsalt reinforced that even discounted assessment, controlling for the mood adjustment that affects content perception this site still reads as substantively above average across multiple pieces I have read carefully today.

  1693. Nicokeeme

    High quality writing, no marketing speak and no buzzwords that mean nothing, and a stop at gambithusk kept that going, simple direct content that actually communicates something is harder to find than it should be and this is one of the rare places that gets it right consistently across many different posts.

  1694. Hughsmets

    Felt this in a way I cannot quite explain, the topic just hit different here, and a stop at gondoenvoy continued in that vein, sometimes you find a site whose perspective lines up with how you have been thinking and reading their work feels like a small relief which I appreciated more than I expected.

  1695. BuddyCisar

    Considered against the flood of similar content this one stands apart in important ways, and a stop at firhush extended that distinctive feel, sites that find their own corner of a crowded topic and stay there are sites worth following and this one has clearly carved out its own space and committed to defending it carefully.

  1696. kyhni SPb_xwSa

    Слушайте кто кухню недавно заказывал Задолбался я уже выбирать То фасады кривые Короче, нашел наконец нормальное производство — заказ кухни с доставкой и сборкой Фасады из влагостойкого МДФ 19 мм В общем, вся инфа вот здесь — глория мебель [url=https://kuhni-spb-uio.ru]https://kuhni-spb-uio.ru[/url] Не ведитесь на салоны в ТЦ Сам столько нервов потратил теперь делюсь

  1697. JoeJutle

    Now adding a small note in my reading log that this site is one to watch, and a look at guavaflank reinforced the watch status, the few sites I track deliberately rather than encounter accidentally are sites I expect ongoing returns from and this one has cleared the bar for that elevated tracking based on what I read.

  1699. Stevensax

    Thanks for the practical examples scattered through the post rather than abstract theory only, and a look at sandaltimber continued that grounded style, abstract points are easier to remember when paired with concrete situations and the writers here clearly understand how readers actually retain information from blog content reading sessions.

  1700. MalcolmSof

    The clarity here is something I really appreciate, especially compared to sites that pile on jargon for no reason, and a look at fortfalcon was the same, simple direct sentences that actually deliver information instead of dancing around the point for paragraphs at a time which wastes reader patience.

  1702. Christopherbleat

    Considered against the flood of similar content this one stands apart in important ways, and a stop at syrupserif extended that distinctive feel, sites that find their own corner of a crowded topic and stay there are sites worth following and this one has clearly carved out its own space and committed to defending it carefully.

  1705. Dexterprook

    The pacing of the post was just right, never rushed and never dragged out unnecessarily, and a look at idleketo maintained the same rhythm, you can tell the writer has experience because the difficult skill of pacing is something only practiced writers manage to handle well in long form content over time and across formats.

  1707. ChaseBof

    Polished and informative without feeling overproduced, that is the sweet spot, and a look at keenfern hit it again, you can tell when a site has been built with care versus thrown together for the sake of having something to put online and this is clearly the former approach taken by the team.

  1709. Omarmib

    Worth observing that the post landed without needing a flashy headline to hook attention, and a stop at swiftswallow did the same, content that earns engagement through substance rather than packaging is the kind I trust more deeply and this site has clearly chosen substance as the primary lever for reader engagement throughout.

  1710. Walterdus

    Felt a small spark of recognition when the post named something I had been struggling to articulate, and a look at swampstaple produced more such moments, the rare service of giving readers language for fuzzy intuitions is one of the higher values that good writing can provide and this site offered several today instances.

  1712. RafaelLok

    Worth flagging this post as worth a careful read rather than a casual skim, and a stop at gamerember earned the same careful approach, the few sites that warrant slower reading are sites I now treat differently from the daily content stream and this one has clearly moved into that elevated treatment category.

  1713. Jayliext

    Worth your time, that is the simplest endorsement I can give, and a stop at gondoiris extends that endorsement across the rest of the site, this is one of those increasingly rare places that delivers on what it promises rather than over selling the content and under delivering on substance every time which I find frustrating elsewhere.

  1715. TrentonPriex

    Reading carefully here has reminded me what reading carefully feels like, and a look at firjuno extended that reminder, the experience of careful reading versus skimming is different in ways I had partially forgotten and this site has clearly refreshed my memory of what attention feels like when content rewards it consistently.

  1716. Caleboweli

    Walked away in a slightly better mood than when I started reading, that says something about the writing, and a stop at vesselthrift kept that going, content that leaves you feeling more capable rather than overwhelmed is the kind I keep coming back to again and again over the years and across many topics.

  1718. LanceJique

    Came here from a search and stayed for the side links because they were that interesting, and a stop at sorbettower took me even further into the site, the kind of organic exploration that good content invites is something most sites kill through aggressive interlinking and pushy navigation choices rather than relying on quality.

  1720. Kalcap

    Started reading without much expectation and ended on a high note, and a look at fossera continued that arc, content that builds rather than peaks early is a sign of a writer who knows how to structure a piece for sustained reader engagement rather than relying on a strong hook to do all the work.

  1722. Spencerundon

    Bookmark added with a small mental note that this is a site to keep, and a look at igloohaze reinforced the keep status, the verb keep rather than visit captures something about how I think about this kind of site and it is a higher tier of relationship than I have with most places online today.

  1723. TristanCub

    Different feel from the algorithmically optimised posts that dominate the topic, and a stop at sagevogue reinforced that human touch, you can tell when a site is being run by someone who reads what they publish versus someone just hitting submit and moving on quickly to the next assignment without checking the result.

  1724. zakazat kyhnu_xbel

    Ребята всем привет. Замучился я уже кухню искать. То доставку три месяца ждать. Короче, единственные кто делает совестливо — купить заказать кухню по чертежам. Гарантия 5 лет на все. В общем, там цены и примеры работ — купить кухню спб [url=https://zakazat-kuhnyu-dfg.ru]купить кухню спб[/url] Проверяйте производителя по этому списку. Сам полгода выбирал теперь знаю.

  1725. Cordellbax

    Reading this confirmed that my time researching the topic in other places had not been wasted, and a stop at shamrockveil extended the confirmation, when independent sources agree that is a useful signal and this site is one of the more reliable sources I have found for cross checking what I read elsewhere on similar subjects.

  1727. JamieShabe

    Just nice to read something that does not feel like it was assembled from a content brief, and a stop at gapherb kept that handcrafted feel going, you can tell when a real human with real understanding is behind the words versus a templated piece churned out for an algorithm to find.

  1728. EddieFurgy

    Adding this site to my regular reading list, the post earned that on its own, and a quick stop at gongflora sealed the decision, the kind of place worth checking back with from time to time because it consistently produces material that holds up against a critical reading too which I really value.

  1729. zakazat kyhnu_uvpt

    Слушайте кто недавно кухню делал. Заколебался я уже выбирать. То доставку месяц ждать. Короче, реальное производство в Питере — купить кухню от производителя в спб недорого. Цены ниже чем в магазинах тысяч на 50. В общем, жмите чтобы не потерять — где лучше купить кухню в спб [url=https://zakazat-kuhnyu-qwe.ru]https://zakazat-kuhnyu-qwe.ru[/url] Не ведитесь на салоны. Сам мучался теперь знаю.

  1730. Finnbeita

    Reading this confirmed that the topic deserves more careful attention than it usually gets, and a stop at firkit extended that elevated framing, content that raises the appropriate weight of a subject without being preachy about it is serving a quiet but important editorial function for the broader cultural conversation about it.

  1731. LandynSwerb

    Looking for similar voices elsewhere has come up empty in my recent searches, and a stop at guavahilt extended the search frustration, the rare site that does what no other does in quite the same way is precious and this one has clearly developed a particular approach that I have not been able to find duplicates of.

  1733. LonnieDaf

    A piece that ended with a clean landing rather than fading out, and a look at keenfoil maintained the same crisp conclusions, endings that resolve rather than dissolve are a sign of careful structural thinking and this site has clearly invested in how its pieces conclude rather than letting them simply run out of energy.

  1734. Jasonjen

    Appreciate how nothing here feels copied or pieced together from other places, the voice is consistent and the tone stays human, and after I checked thrashurge I noticed the same style holds, which is a small detail but it makes the whole experience feel personal rather than like another generic site.

  1736. NickNor

    A nicely understated post that does not shout for attention, and a look at irisetch maintained the same quiet quality, understatement is a stylistic choice that distinguishes serious writing from attention seeking writing and this site has clearly committed to the understated approach as a core editorial value rather than just a phase.

  1737. zakazat kyhnu_ursr

    Народ привет. Задолбался я выбирать кухню. Короче, единственные кто не наебывает — заказать кухню без переплат. Фурнитура Blum. В общем, вся инфа здесь — купить заказать кухню [url=https://zakazat-kuhnyu-bnm.ru]купить заказать кухню[/url] Проверяйте производителя. Перешлите тому кто ищет.

  1739. RichardSeext

    This stands out compared to similar posts I have read recently, less noise and more substance, and a look at tailortarget kept that gap going, you can really feel the difference between content made by someone who cares versus content made to fill a publishing schedule for an algorithm trying to keep growing somehow.

  1740. Egancus

    Genuinely glad I clicked through to read this rather than skipping past, and a stop at fossgusto confirmed I should keep clicking through to more pages here, the kind of resource that justifies its place in my browser history rather than feeling like wasted time which is the highest compliment I offer any site online today.

  1742. Brentvot

    Genuinely glad I clicked through to read this rather than skipping past, and a stop at topazstrict confirmed I should keep clicking through to more pages here, the kind of resource that justifies its place in my browser history rather than feeling like wasted time which is the highest compliment I offer any site online today.

  1743. CraigWhord

    Felt the writer did the homework before publishing, the references hold up, and a look at gapjumbo continued that documented care, content with traceable claims rather than vague assertions is the kind I trust and the lack of bald assertion in this post is one of its quietly impressive qualities for me.

  1744. Jorgesuere

    A piece that handled a controversial angle without becoming heated, and a look at gonggrip continued that calm engagement, content that can address contested topics without inflaming them is doing rare diplomatic work and this site has clearly developed the editorial maturity to handle sensitive material with the appropriate temperature of writing throughout.

  1745. Johnvup

    Reading this in a relaxed evening setting was a small pleasure, and a stop at sauntersonar extended the pleasant evening reading, content that fits the tone of relaxed time without becoming forgettable is what I look for in evening reading and this site has the right tone for that particular slot in my daily reading routine.

  1746. VictorJaisy

    Now feeling the post has earned a proper recommendation rather than a casual mention, and a stop at flameeden reinforced the recommendation strength, the difference between mentioning and recommending is a small editorial distinction I observe in my own conversations and this site has earned the upgraded recommendation level from me confidently today.

  1748. Jamelhor

    If I had to summarise the editorial sensibility of this site in a few words it would be careful and human, and a look at irisgusto extended that summary feeling, capturing the essence of a sites approach in brief is hard but this site has a clear enough identity that the summary comes naturally enough.

  1749. Omaramola

    Adding this to my list of go to references for the topic, and a stop at sorbetsolo confirmed the rest of the site deserves the same, definitely the kind of resource that earns its place rather than getting forgotten the moment the next interesting article shows up in my feed somewhere else on the web.

  1751. kyhni SPb_cxSa

    Люди помогите советом Задолбался я уже выбирать То фасады кривые Короче, нашел наконец нормальное производство — купить кухню в спб от производителя недорого Цены ниже чем в салонах тысяч на 30 В общем, смотрите сами по ссылке — кухни на заказ в санкт-петербурге [url=https://kuhni-spb-uio.ru]https://kuhni-spb-uio.ru[/url] Не ведитесь на салоны в ТЦ Сам столько нервов потратил теперь делюсь

  1753. Jamesenund

    Just sat with this for a bit longer than I usually would because the points are worth thinking about, and after tidalslick I had even more to chew on, the kind of post that nudges your thinking forward without forcing the issue is something I have always appreciated in good writing online.

  1754. kyhni SPb_mgMa

    Всем привет из культурной столицы Цены задрали как на золото То ДСП крошится Короче, реальное производство в Питере — кухни СПб от производителя напрямую Цены ниже салонов на 40 тысяч В общем, смотрите сами по ссылке — кухни на заказ в спб недорого [url=https://kuhni-spb-fpk.ru]кухни на заказ в спб недорого[/url] Проверяйте производителя по этому списку Сам полгода выбирал теперь знаю

  1756. Lancetuh

    Bookmark folder created specifically for this site, and a look at kelpfancy confirmed the dedicated folder was the right call, dedicated folders for individual sites are a level of organisation I rarely deploy and this site has earned that level of dedicated tracking based on the consistency I have seen so far across sessions.

  1758. MichaelDut

    Now thinking about whether the writer might publish a longer form work I would buy, and a look at framegable suggested the same depth would translate, content that makes me want to pay for related work in other formats is content that has earned commercial trust as well as attention trust and this site has both clearly.

  1759. Coenfoupe

    Now thinking about whether the writer might publish a longer form work I would buy, and a look at gapkraft suggested the same depth would translate, content that makes me want to pay for related work in other formats is content that has earned commercial trust as well as attention trust and this site has both clearly.

  1760. DarylTReva

    Quietly enjoying that I have found a new site to follow for the topic, and a look at gongjade reinforced the small pleasure of the find, the discovery of new high quality sources is one of the more durable pleasures of careful internet reading and this site has been generating that discovery pleasure at multiple points already today.

  1761. EarlMiz

    Really like the way the post resists reaching for cliches that would have made it feel generic, and a quick visit to gulfflux kept that fresh feel going, original phrasing and unexpected metaphors are signs that the writer is actually thinking rather than just stitching together familiar phrases into the appearance of content.

  1762. CedricMourl

    Thank you for keeping the writing honest and the points easy to verify against your own experience, and a stop at tennisvortex reflected the same approach, no exaggeration just steady useful content that I can take with me into my own work without second guessing every sentence I happen to read here.

  1763. Willisdot

    Recommended without hesitation if you care about careful coverage of this topic, and a stop at ironfleet reinforced the recommendation, the bar I set for unhesitating recommendations is fairly high and this site has cleared it through the cumulative weight of multiple consistently good pieces rather than through any single standout post which is meaningful.

  1764. Johanniz

    Considered against the flood of similar content this one stands apart in important ways, and a stop at flankgate extended that distinctive feel, sites that find their own corner of a crowded topic and stay there are sites worth following and this one has clearly carved out its own space and committed to defending it carefully.

  1766. kyhni SPb_dkOn

    Ребята всем привет Замучился я уже кухню искать То фасады покоробились от пара Короче, реальный цех в СПб без наценок — кухни на заказ в спб с фурнитурой Blum Цены ниже рыночных на треть В общем, вся инфа вот тут — кухня по индивидуальному проекту [url=https://kuhni-spb-ytr.ru]https://kuhni-spb-ytr.ru[/url] Проверяйте производителя по этому списку Перешлите другу кто тоже мучается

  1767. Lucasviomb

    A piece that was confident enough to leave some questions open rather than forcing closure, and a look at trenchvinca continued that intellectual honesty, content that admits the limits of its scope is more trustworthy than content that pretends to total understanding and this site has the right calibration on certainty consistently.

  1768. kyhni SPb_jhsr

    Народ всем привет Прошерстил 30 салонов — везде перекупы То ДСП сыпется Короче, реальное производство в Питере — купить кухню в спб от производителя с установкой Замер на следующий день В общем, вся инфа вот здесь — кухни на заказ производство спб [url=https://kuhni-spb-nbg.ru]кухни на заказ производство спб[/url] Проверяйте производителя по этому списку Перешлите тому кто тоже мучается

  1769. Stevenvap

    Thanks for laying this out in a way that someone newer to the topic can follow, and a stop at scrolltower kept that accessibility going, writing that meets readers at different experience levels without condescending is hard to do well and the writers here have clearly thought about who they are writing for.

  1772. MikeadjuB

    Reading this gave me a quiet moment of intellectual pleasure that I had not been expecting, and a stop at vectorswift extended that pleasure across more pages, the unexpected reward of stumbling into careful writing is one of the small ongoing pleasures of reading the open web and this site is delivering it reliably.

  1775. GerardoLop

    Beyond the topic at hand this site reads as a small ongoing project of taking writing seriously, and a look at gaussfawn reinforced that project quality, sites that treat publishing as an ongoing serious practice rather than as content production for traffic are sites worth supporting and this one has clearly chosen the serious approach.

  1777. Lawsonkar

    Reading carefully here has reminded me what reading carefully feels like, and a look at ironkrill extended that reminder, the experience of careful reading versus skimming is different in ways I had partially forgotten and this site has clearly refreshed my memory of what attention feels like when content rewards it consistently.

  1778. Duncankef

    Now planning a longer reading session for the archives, and a stop at frescoheron confirmed the archives are worth that longer commitment, sites with archives I want to read deliberately rather than just sample are rare and this one has clearly earned that level of interest based on the consistency of what I have already read.

  1779. Harlansmilk

    Reading this in the gap between work projects was a small but meaningful break, and a stop at gongketo extended that gentle reset, content that provides genuine refreshment rather than just distraction during work breaks is content with a particular kind of utility and this site fits that role for me reliably during work days.

  1780. Wendellpadok

    Felt the post had been written without looking over its shoulder, and a look at flankhaven continued that confident posture, content written for its own sake rather than against imagined critics has a different quality and this site reads as written from a place of confidence rather than defensive justification of every claim.

  1781. JamelSwini

    Now considering the post as evidence that careful blog writing is still possible, and a look at unicorntempo extended that evidence, the broader question of whether the modern web can sustain quality writing has obvious empirical answers in sites like this one and seeing them is reassuring even when they remain a minority overall today.

  1783. Douglassog

    Appreciated that the writer trusted the reader to follow along without constant restating of earlier points, and a look at kelpgrip continued that respect for the reader, treating an audience as capable adults rather than as people to be hand held through every paragraph is something I notice and value highly across the open internet today.

  1784. KentonTib

    Closed the tab with a small sense of finality rather than the usual rushed exit, and a stop at teapotshrine produced the same considered closing, when reading ends with deliberate satisfaction rather than impatient skip you know the time was well spent and this site is producing those satisfying endings consistently across what I read.

  1786. Rodolfowek

    A piece that read as if the writer was thinking carefully rather than just typing fluently, and a look at surgesorrel continued that considered quality, the difference between fluent typing and careful thinking shows up in writing and this site reads as the product of thought rather than just the product of language fluency apparently.

  1787. kyhni SPb_giol

    Доброго времени Цены космос а качество мыло То кромка отклеивается через месяц Короче, единственные кто не наваривается в тридорога — кухни СПб напрямую от производителя Кромка на немецком оборудовании В общем, смотрите сами по ссылке — заказ кухни [url=https://kuhni-spb-wxh.ru]заказ кухни[/url] Не ведитесь на салоны в ТЦ которые просто заказывают у китайцев и ставят наценку 100% Перешлите тому кто тоже мучается выбором

  1788. zakazat kyhnu_ycel

    Ребята всем привет. Менеджеры врут про сроки и материалы. То фасады покоробились от пара. Короче, нашел нормальных производителей — купить кухню в спб с установкой. Кромка ПВХ 2 мм немецкая. В общем, там цены и примеры работ — купить кухню от производителя в спб [url=https://zakazat-kuhnyu-dfg.ru]купить кухню от производителя в спб[/url] Проверяйте производителя по этому списку. Перешлите другу кто тоже мучается.

  1792. Morgandaw

    Thanks for not padding this with the usual filler intros and outros that every other blog seems to require, and a quick visit to ironkudos continued that lean approach across more posts, content stripped of waste is content that respects you and I will always come back to that kind of approach.

  1793. BernardApaks

    Will be sharing this with a couple of people who care about the topic, and a stop at gausskite added more material worth passing along, the kind of site that is generous with quality content and does not make you jump through hoops to access it which is appreciated more than the team probably realises.

  1796. RolandoMitle

    Just enjoyed the experience without needing to think about why, and a look at gulfholm kept that effortless feeling going, sometimes the best content is invisible in the sense that you forget you are reading until you reach the end and realise time has passed without you noticing it pass naturally.

  1797. KirkRilia

    Without comparing too aggressively to other sources this one stands out for the right reasons, and a look at gooseholm continued that distinctive quality, content that distinguishes itself through substance rather than style tricks is content with lasting differentiation and this site has clearly chosen substance based differentiation as its core editorial strategy.

  1798. Samuelfrecy

    Started reading and ended an hour later without realising the time had passed, and a look at flankisle produced the same time dilation effect, when content makes time feel different the writer has achieved something well beyond the average and this site is producing that experience for me reliably across multiple readings.

  1799. Omarmib

    Walked away with a clearer head than I had before reading this, and a quick visit to swiftswallow only sharpened that, the writing has a way of cutting through the noise that surrounds most topics online which is something I will definitely remember the next time I am searching for an answer to anything.

  1800. kyhni SPb_srMa

    Всем привет из культурной столицы Задолбался я уже кухню искать То ручки отваливаются через месяц Короче, мужики с руками из нужного места — кухни СПб от производителя напрямую Замер на следующий день В общем, вся инфа вот здесь — кухни на заказ спб недорого с ценами [url=https://kuhni-spb-fpk.ru]https://kuhni-spb-fpk.ru[/url] Не ведитесь на салоны-прокладки с наценкой 100% Сам полгода выбирал теперь знаю

  1801. Davonbiage

    Speaking carefully because I do not want to overstate things this site is genuinely above average across multiple measurements, and a stop at frondketo continued the above average performance, the calibration of judgement against potential overstatement is something I take seriously and this site clears the higher bar even after that calibration applies.

  1802. EddieNatry

    However selective I am about new bookmarks this one made it past my filter, and a look at shoresyrup confirmed the bookmark was worth the slot, the precious slots in my permanent bookmark folder are difficult to earn and this site earned one without making me think twice about whether the slot was justified by the quality.

  1803. IsaiahGaf

    Picked this up while looking for something else and ended up reading every paragraph because it was actually informative, and after shoreskipper I was sure I would come back, that does not happen often when most sites bury the useful parts under endless ads and pop ups today and across most categories online.

  1804. OscarEscon

    Came in skeptical of the angle and left mostly persuaded, and a stop at shamrockswan pushed me a bit further in the same direction, content that can move a critical reader by argument rather than rhetoric is rare and worth pointing out because it indicates real substance underneath the surface presentation here.

  1805. Vaughnicove

    Reading this slowly because the writing rewards a slower pace, and a stop at vitalsnippet did the same, the pace at which I read content is something I now use as a quality signal and writing that earns a slower pace earns my attention as a reader looking for substance these days.

  1808. solana_gqOi

    Erlebe jetzt aufregende Gewinne im [url=https://solonlinecasino.de/]bestes solana online casino[/url] und sichere dir exklusive Boni.
    Spieler schatzen die schnellen Transaktionen und niedrigen Gebuhren, die Solana bietet.

  1809. CarmeloAnned

    During a quiet evening reading session this provided just the right depth without being heavy, and a stop at gemglobe maintained the same evening appropriate weight, content with depth that does not exhaust the reader is content with editorial calibration and this site has clearly figured out how to be substantial without being demanding all the time.

  1810. zakazat kyhnu_gkSt

    Народ привет. Вечно то цены конские у дилеров. Объездил уже кучу салонов — тьфу. Короче, единственные кто не наебывает — купить кухню от производителя в спб с доставкой. Замерщик приехал на следующий день. В общем, жмите чтобы не потерять контакты — купить кухню в спб [url=https://zakazat-kuhnyu-gkl.ru]купить кухню в спб[/url] Проверяйте производителя в этом списке. Сам полгода мучился теперь делюсь.

  1815. Raymondhag

    Worth saying that the post fit naturally into a rhythm of careful reading, and a stop at flankivory extended the same rhythm, content that pairs well with how I actually read rather than demanding a different mode is content well calibrated to its likely audience and this site has clearly thought about that consistently.

  1816. Stuartvam

    Excellent execution from start to finish, the post never loses its rhythm and the points stay sharp, and a quick stop at stitchvamp kept the same level going, consistency like this across a site is the marker of a serious operation rather than a casual side project running on autopilot somewhere else.

  1817. NedUsels

    Decided this was the best thing I had read all morning, and a stop at gorgefair kept that ranking intact, ranking my reading is something I do mentally throughout the day and the top rank is competitive and not easily won but this site won it without needing to overstate its claims for that.

  1819. WilsonAbive

    Reading this gave me something to think about for the rest of the afternoon, and after taffetaswan I had even more to mull over, the kind of post that lingers in the background of your day rather than evaporating immediately is genuinely valuable in an attention economy that punishes depth rather than rewarding it.

  1820. KaiKeedA

    Thanks for the simple approach, too many sites bury the actual point under layers of unnecessary words, but here every line earns its place, and a look at fumefig showed the same care for the reader which is something I will remember the next time I need answers on a topic.

  1821. RodolfoLip

    Honest take is that this was better than I expected when I clicked through, and a look at summitshire reinforced that, the bar for online content has dropped so much that finding something thoughtful and well constructed feels almost noteworthy now which says more about the average than about this site itself.

  1823. HarlanCause

    Liked the way the post balanced confidence and humility, and a stop at sofatavern maintained the same balance, knowing when to assert and when to acknowledge uncertainty is a sign of mature thinking and the writers here have clearly developed that calibration through what I assume is years of careful work on their craft.

  1825. TravisBendy

    Honest reaction is that this is the kind of writing I would defend in a conversation about good blog content, and a look at genieframe reinforced that, the rare site whose work I would actively recommend rather than just tolerate is the kind I want to support through return visits regularly.

  1826. JordanSluby

    Now appreciating that the post did not require me to agree with the writer to find it valuable, and a look at islegoal maintained the same useful regardless of agreement quality, content that informs even when it does not convince is content with broader utility and this site reads as useful even when I disagree.

  1828. KnoxMuh

    Found a small mental shift after reading this, the framing here is just a bit different from the standard takes online, and a look at kelpherb extended that fresh perspective across more material, the rare site whose voice actually changes how you think about something rather than just confirming existing beliefs.

  1829. Angeltoino

    Now adjusting my mental list of reliable sites for this topic, and a stop at thisdomainisdishk reinforced the adjustment, the small ongoing curation work of maintaining trusted sources is one of the actual practical activities of careful reading and this site has earned a permanent place on my list for this particular subject.

  1830. BrockBok

    Definitely returning here, that is decided, and a look at gulfkoala only made the case stronger, this is one of those rare websites that rewards regular visits rather than feeling stale after the first read which is something I cannot say about most of the places I bookmark today across all my topics.

  1831. kyhni SPb_yrSa

    Народ всем привет Задолбался я уже выбирать То кромка отклеивается через месяц Короче, единственные кто не наваривается в тридорога — кухни СПб от производителя напрямую Кромка на немецком оборудовании В общем, сохраняйте себе в закладки — кухни на заказ в спб [url=https://kuhni-spb-uio.ru]кухни на заказ в спб[/url] Не ведитесь на салоны в ТЦ Сам столько нервов потратил теперь делюсь

  1833. Leonardgaf

    Speaking as someone who used to recommend blogs frequently and got out of the habit this site is rekindling that impulse, and a look at gorgeheron extended the rekindling, the recovery of an old habit triggered by encountering work that justifies it is itself a small kind of pleasure and this site is providing that recovery experience.

  1834. LorenzoWrild

    Genuine reaction is that I will probably think about this on and off for a few days, and a look at flaskkelp added fuel to that, the best content lingers in your head after you close the tab rather than evaporating immediately and this site clearly knows how to write that kind of memorable content.

  1835. ShermanPeefs

    A piece that brought a sense of order to a topic I had been finding chaotic, and a look at safaritriton continued that organising effect, content that imposes useful structure on messy subjects is doing genuine intellectual work and this site is providing that organisational function across multiple posts I have read recently here.

  1836. ForrestCaumn

    Honestly the simplicity is what makes this work, the topic is not buried under filler words or overly complex examples, and a quick look at stencilveto showed the same sensible style, I left with what I came for and no headache from over reading which is a real win these days.

  1837. kyhni SPb_iuol

    Всем привет из Питера Продаваны врут про материалы То фасады кривые с зазорами Короче, нашел наконец нормальное производство — заказать кухню по индивидуальным размерам Сделали 3D-проект бесплатно за час В общем, смотрите сами по ссылке — производство кухонь в спб на заказ [url=https://kuhni-spb-wxh.ru]https://kuhni-spb-wxh.ru[/url] Не ведитесь на салоны в ТЦ которые просто заказывают у китайцев и ставят наценку 100% Сам столько нервов потратил теперь делюсь опытом

  1838. TristanJaite

    Started forming counter examples to test the claims and the post handled most of them implicitly, and a look at vandaltavern continued that anticipatory style, writers who think two steps ahead of the critical reader save themselves from a lot of follow up work and this writer has clearly internalised that habit consistently.

  1839. Jadendex

    Thanks for keeping things clear and to the point, that is honestly hard to find online these days, and after reading through velourturban the message stayed consistent which makes me trust the information being shared more than I usually do on similar pages that cover this same kind of topic.

  1840. JavonChips

    Honestly impressed by how much useful content sits in such a small post, and a stop at fumefinch confirmed the rest of the site packs a similar punch, density without confusion is a hard balance to strike and this site has clearly cracked the code on it across many different topic areas covered.

  1841. RaymondCoilt

    A piece that earned its conclusions through the body rather than asserting them at the end, and a look at jadeflax maintained the same earned quality, conclusions that follow from what came before are more persuasive than declarations and this site has clearly internalised that principle in how it constructs arguments throughout pieces.

  1843. Timmygoove

    This filled in a gap in my understanding that I had not even noticed was there, and a stop at gladfir did the same, the kind of post that gives you more than you expected when you first clicked through from somewhere else, a real find for anyone curious about the area covered here.

  1845. Keanuplats

    During the time spent here I noticed the absence of the usual distractions, and a stop at solotoffee extended that distraction free experience, content that does not fight my attention with pop ups and modals and aggressive prompts is content that respects me and this site has clearly chosen the respectful approach throughout.

  1848. QuentinWah

    Really liked the calm tone running through the post, no shouting and no urgency forced into the writing, and a look at gorgeivy kept that quiet confidence going, the kind of voice that makes the reader feel respected rather than yelled at which is depressingly common across most modern blog content these days.

  1849. KnoxDisse

    Reading more of the archives is now on my plan for the weekend, and a stop at flintgala confirmed the archive worth the time, the rare archive worth a dedicated reading session rather than just casual sampling is the rare archive of serious work and this site has clearly produced enough of that work to warrant the deeper exploration.

  1851. Amarifap

    Worth pointing out the careful word choice in this post, no buzzwords and no jargon, and a look at shrinetender continued that disciplined vocabulary, sites that resist the pull of trendy language are sites that will read well in five years and this one is clearly built for that kind of long durability.

  1852. Edgarmam

    Reading this slowly and letting each paragraph land before moving on, and a stop at jetfrost earned the same patient approach, content that rewards slow reading rather than speed is content with real density and the writers here are clearly producing work that benefits from the careful eye rather than the rushed scan.

  1853. Lancebaf

    Came away with some new perspectives I had not considered before, and after ketohale those ideas felt more complete, the kind of content that stays with you a little while after reading rather than slipping out the moment you switch tabs and move on with your day to whatever comes next.

  1855. Quinnbut

    Reading this gave me a small mental break from the heavier reading I had been doing, and a stop at fumegrove extended that lighter feel, content that provides relief without becoming trivial is harder to produce than people realise and this site has clearly figured out how to be light without being shallow at all.

  1856. Quincywew

    The pacing of the post was just right, never rushed and never dragged out unnecessarily, and a look at gladhalo maintained the same rhythm, you can tell the writer has experience because the difficult skill of pacing is something only practiced writers manage to handle well in long form content over time and across formats.

  1859. Jackwairl

    Skipped breakfast still reading this and finished hungry but satisfied, and a stop at slacktally kept me past breakfast time, content that displaces basic biological needs is content with serious attentional pull and the writers here are clearly capable of producing that level of engagement which is genuinely impressive these days.

  1860. DwightCable

    A piece that did exactly what it promised in the headline without overshooting or underdelivering, and a look at silovault continued that calibration, alignment between promise and delivery is a basic editorial virtue that many sites fail at and this site has clearly mastered the matching of expectation and substance throughout pieces.

  1861. EmilioAddib

    Even on a quick first read the substance of the post comes through, and a look at herbharp reinforced that immediate quality, content that does not require a slow careful read to demonstrate value but rewards one anyway is content with real depth and this site has produced work of that demanding depth class.

  1862. kyhni SPb_hpMa

    Приветствую Задолбался я уже кухню искать То ДСП крошится Короче, нашел наконец нормальную контору — заказ кухни с установкой Проект бесплатно за час В общем, там цены и каталог работ — кухни на заказ в спб от производителя [url=https://kuhni-spb-fpk.ru]кухни на заказ в спб от производителя[/url] Не ведитесь на салоны-прокладки с наценкой 100% Сам полгода выбирал теперь знаю

  1863. Marlonbiorm

    Liked the way the post balanced confidence and humility, and a stop at gullgoal maintained the same balance, knowing when to assert and when to acknowledge uncertainty is a sign of mature thinking and the writers here have clearly developed that calibration through what I assume is years of careful work on their craft.

  1864. Jadendex

    Ended up here on a wandering afternoon and was glad I stayed for the read, and a stop at velourturban extended the wandering into a proper exploration of the site, the kind of place that rewards aimless clicking with something genuinely interesting rather than the shallow content that mostly populates the modern open web.

  1865. Troymem

    Halfway through I knew I would finish the post, and a stop at goshfrost also held me through to the end, content that signals its quality early and then sustains it is content with real internal consistency and this site has clearly figured out how to maintain quality from opening sentence through to closing thought.

  1866. Ernestowapse

    Thanks for the readable length, I finished it without checking how much was left, and a stop at flockergo kept me reading the same way, when I stop noticing the length of a piece because the content is engaging enough to sustain attention without willpower the writer has done their job well today.

  1870. Christianvoica

    Now thinking I want more sites built on this kind of editorial foundation, and a stop at sampleshadow extended that wish into a broader hope, sites built on substance and care rather than on metrics and growth are the kind of sites I want to see more of and this one is a small example worth supporting.

  1871. CliffordDuesy

    A clear case of writing that does not try to do too much in one post, and a look at jetivory maintained the same scoped discipline, posts that try to cover too much end up covering nothing well and this site has clearly chosen scope discipline as a core editorial principle which shows up clearly in what I read.

  1873. DavonLop

    Quietly building a case in my head for why this site deserves more attention than it currently seems to receive, and a look at tundrasyrup reinforced the case, the gap between quality and recognition is a recurring frustration in independent online content and this site is one of the cases that seems particularly egregious to me today.

  1876. Ricosteme

    Big thanks to whoever wrote this, you saved me a lot of time hunting for the same info on other sites, and a stop at senatetoucan only added more useful detail without going off topic, that kind of focus is honestly hard to come across these days when most posts wander everywhere.

  1878. Otisbrilk

    The tone stayed consistent across the whole post which is harder than it looks for longer pieces, and a look at glazeflask continued the same voice, this kind of editorial consistency is a sign of either a single careful writer or a tightly run team and either is impressive today across the broader media environment.

  1879. AidanPring

    Liked that there was nothing performative about the writing, and a stop at fumehull continued that genuine quality, performative writing tries to be witnessed rather than read and the difference between performance and substance is huge for the careful reader and this site has clearly chosen substance every time clearly.

  1880. LeeDox

    Honestly enjoyed reading this more than I expected to when I first clicked through, and a stop at ketojib kept that pleasant surprise going, sometimes you stumble onto a site that just clicks with how you like to read and this is one of those for me right now today which is great.

  1881. ScottTof

    If I were to recommend a starting point for the topic this site would be near the top of my list, and a stop at tealthicket reinforced that recommendation status, the small list of starting point recommendations I keep for friends asking about topics is short and this site is now firmly on it.

  1882. Bradkex

    Glad to find something on this topic that does not start with three paragraphs of throat clearing before getting to the point, and a stop at solacesteam also dives right in, respect for the readers time shows up in small editorial choices like this and they add up to a real difference quickly.

  1885. Randybon

    Closed the laptop after this and let the ideas settle for a few hours, and a stop at grebeflame similarly rewarded reflective time, content that benefits from sitting with rather than racing past is the kind I want more of and the kind that this site appears to consistently produce week after week here.

  1886. Tomtug

    Granted I am giving this site more credit than I usually give new finds, and a look at flockfine continued earning that credit, the calibration of how much trust to extend after limited exposure is something I do carefully and this site has earned more trust on shorter exposure than most due to consistent quality across.

  1887. CarlPiege

    Found the use of subheadings really helpful for scanning back through the post later, and a stop at tallysubdue kept that reader friendly approach going, navigation is something many blog writers ignore but small structural choices make a noticeable difference for someone returning to find a specific point again days or weeks later.

  1888. EdgarIcorp

    Cuts through the usual marketing fluff that dominates this topic online, and a stop at jibfig kept the same clean approach going, this is the kind of writing that respects the reader’s time rather than wasting it on repetitive setups before finally getting to the point at hand which is what most sites do.

  1889. Jadendex

    Speaking from the perspective of a fairly demanding reader the writing here clears the bar consistently, and a look at velourturban continued clearing that bar, the calibration of demanding reader is something I apply to all sources and this site has been one of the few that handles the demanding reading well across pieces sampled.

  1891. EmilioAddib

    Even on a quick first read the substance of the post comes through, and a look at herbharp reinforced that immediate quality, content that does not require a slow careful read to demonstrate value but rewards one anyway is content with real depth and this site has produced work of that demanding depth class.

  1892. DarrenDek

    Skipped the comments to avoid spoilers and came back later to find them genuinely worth reading, and a stop at solidtiger extended that surprised respect, when the discussion below a post matches the quality of the post itself you have found something special and this site appears to attract that kind of audience.

  1895. Rickmek

    A piece that did not lecture even when it had clear positions, and a look at siennathrift maintained the same teaching without preaching tone, finding the line between informing and lecturing is hard and most sites land on the wrong side of it but this one has clearly figured out how to inform without becoming preachy.

  1896. LeonardGag

    Quality writing that respects the reader’s intelligence without overloading them, and a quick look at gleamjuly reflected that approach, a balanced thoughtful site that earns trust by being consistent rather than by shouting about how trustworthy it is which is the usual approach online sadly across most content categories.

  1897. Christianvoica

    Just want to say thank you for putting this together, posts like these make searching online actually worth it sometimes, and a quick look at sampleshadow kept that going, useful and easy to read without any of the tricks that ruin most blog comment sections lately on the wider open web.

  1900. TrevorEsore

    Speaking as someone who used to recommend blogs frequently and got out of the habit this site is rekindling that impulse, and a look at suburbvesper extended the rekindling, the recovery of an old habit triggered by encountering work that justifies it is itself a small kind of pleasure and this site is providing that recovery experience.

  1902. AveryBelia

    Worth observing that the post landed without needing a flashy headline to hook attention, and a stop at gullkindle did the same, content that earns engagement through substance rather than packaging is the kind I trust more deeply and this site has clearly chosen substance as the primary lever for reader engagement throughout.

  1903. Trentorami

    Now realising the post has been quietly doing important work in my mind for the past hour, and a stop at jouleforge extended that quiet processing, content that continues to do work after I close the tab is content with afterlife in the mind and this site is producing those long lived effects at a meaningful rate.

  1904. Carmineeromy

    A piece that read smoothly because the writer understood how readers actually move through prose, and a look at furlkale maintained the same reader awareness, writers who think about the reading experience as much as the writing experience produce better work and this site has clearly made that shift in editorial approach.

  1905. Nathanrok

    Loved the writing voice here, friendly without being fake and confident without being arrogant, and a stop at grebeheron carried the same tone forward, the kind of personality that makes a reader feel welcome rather than lectured at which is a balance plenty of writers struggle to find no matter how long they have been at it.

  1906. Roccoalame

    This stands out compared to similar posts I have read recently, less noise and more substance, and a look at flockgala kept that gap going, you can really feel the difference between content made by someone who cares versus content made to fill a publishing schedule for an algorithm trying to keep growing somehow.

  1907. TylerBlisk

    If a friend asked me where to read carefully on the topic I would send them here without hesitation, and a look at tangovillage confirmed the recommendation strength, the directness of my recommendation reflects how confident I am in the quality and this site has earned undiluted recommendations from me across multiple recent conversations actually.

  1908. kyhni SPb_ztol

    Всем привет из Питера Прошерстил кучу салонов — везде одни перекупы То кромка отклеивается через месяц Короче, нашел наконец нормальное производство — кухни в спб от производителя из массива Замерщик приехал на следующий день В общем, там каталог с ценами и реальные отзывы — мебель для кухни спб от производителя [url=https://kuhni-spb-wxh.ru]https://kuhni-spb-wxh.ru[/url] Проверяйте производителя по этому списку Сам столько нервов потратил теперь делюсь опытом

  1910. Mariodieta

    However selective I am about new bookmarks this one made it past my filter, and a look at tractshade confirmed the bookmark was worth the slot, the precious slots in my permanent bookmark folder are difficult to earn and this site earned one without making me think twice about whether the slot was justified by the quality.

  1911. Milotearl

    Quality writing that respects the reader’s intelligence without overloading them, and a quick look at steamstraw reflected that approach, a balanced thoughtful site that earns trust by being consistent rather than by shouting about how trustworthy it is which is the usual approach online sadly across most content categories.

  1912. OscarRap

    Approaching this with the usual skepticism I bring to new sites and being slowly persuaded, and a stop at creekharbormerchantgallery continued that gradual persuasion, the careful path from skeptical reader to genuine fan is the only one I trust and this site has walked me along that path through patient consistent quality across pieces.

  1913. IssacRor

    Thanks for treating the topic with the seriousness it deserves without becoming pompous about it, and a stop at sculptsilver continued that balanced treatment, the gap between earnest and self serious is huge and writers who can stay on the right side of it earn my respect when I find them online today.

  1915. Daxsic

    Most blog writing on this subject reaches for the same handful of arguments and this post avoided them, and a look at solotopaz continued the original treatment, content that finds its own path through territory other writers have flattened is content with real authorial energy and this site has plenty of that distinctive energy.

  1916. ArnoldoBaida

    Glad I gave this a chance instead of bouncing on the headline, and after ketojuly I was certain I had made the right call, snap judgements based on titles miss a lot of good content and this is a reminder to slow down and check things out before scrolling past in a hurry.

  1918. MaxLOB

    Picked up a couple of new ideas here that I can actually try out, and after my visit to halbrook I have even more notes saved, this is the kind of resource that pays you back for the time you spend on it which is rare to come across in this corner of the web.

  1919. Rickmek

    After several visits I am now confident this site is one to follow seriously, and a stop at siennathrift reinforced that confidence, the gradual building of trust through repeated quality exposures is the only sustainable way to develop reader loyalty and this site is building that loyalty in me through patient consistent work consistently.

  1920. LoganMow

    Took the time to read every paragraph rather than skimming for the punchline, and a quick visit to heronfoil earned the same careful attention from me, that is the highest signal I can give about content quality because my default mode is rapid scanning rather than deliberate reading on most pages.

  1921. KyrieChuts

    Solid little post, the kind that does not need to be flashy because the substance is doing the work, and a look at glenfir kept that quiet confidence going across the site, this is what writing looks like when the writer trusts the content to land on its own without theatrics or unnecessary attention seeking behaviour.

  1922. CedricLinnY

    Reading this gave me a quiet moment of intellectual pleasure that I had not been expecting, and a stop at joustglade extended that pleasure across more pages, the unexpected reward of stumbling into careful writing is one of the small ongoing pleasures of reading the open web and this site is delivering it reliably.

  1923. JoseDut

    Reading this between two meetings turned out to be the highlight of the morning, and a stop at verminturbo continued that highlight quality, content that outshines the structured parts of a working day is doing something well beyond ordinary and this site has produced multiple such highlights for me already this week alone.

  1924. Dalecob

    Felt the writer was being honest with the reader which is rare enough that I want to acknowledge it, and a look at soontornado continued that honest feel, content built on actual knowledge rather than aggregated summaries is something I value highly and rarely come across in regular searches on the open internet these days.

  1925. EnzoRoork

    Liked the way the post handled the final paragraph, no neat bow but no abrupt cutoff either, and a stop at grebeknot continued that thoughtful ending pattern, endings are hard and most blog writers either over engineer them or skip them entirely and this site has clearly figured out a sustainable middle approach.

  1926. JamalLaw

    Now appreciating the small but real way this post improved my afternoon, and a stop at floeiron extended that small improvement effect, content that produces measurable positive impact on the texture of a reading day is content with real value and this site is producing those small positive impacts at a sustainable rate apparently.

  1928. MosesIntix

    During a quiet evening reading session this provided just the right depth without being heavy, and a stop at gablejuno maintained the same evening appropriate weight, content with depth that does not exhaust the reader is content with editorial calibration and this site has clearly figured out how to be substantial without being demanding all the time.

  1929. StuartIsolo

    Even from a single post the editorial care is clear, and a stop at syruptarot extended that care across more pages, the kind of attention to quality that shows up in every paragraph is what separates serious sites from the rest and this one has clearly invested in that paragraph level attention across what I have read.

  1930. KelbyLoatt

    A piece that handled a controversial angle without becoming heated, and a look at serifveil continued that calm engagement, content that can address contested topics without inflaming them is doing rare diplomatic work and this site has clearly developed the editorial maturity to handle sensitive material with the appropriate temperature of writing throughout.

  1931. Grantrem

    A clear cut above the usual noise on the subject, and a look at tigerteacup only made that gap wider in my view, the kind of place that earns its visitors through quality rather than through aggressive marketing or sponsored placements which is increasingly the only way most sites stay afloat across the modern web.

  1933. DavionJuddy

    A relief to read something where I did not have to fact check every claim mentally, and a look at subletviper continued that reliable feeling, sites where I can lower my guard and trust the content are rare and this one is earning that trust paragraph by paragraph through consistent careful work behind the scenes.

  1934. EmanuelTub

    Following the post through to the end without my attention drifting once, and a look at crowncovemerchantgallery earned the same uninterrupted attention, content that holds attention without manipulating it is content with substantive pull and this site has demonstrated that substantive pull across multiple pieces in a single reading session reliably here today.

  1935. kyhni SPb_scsr

    Слушайте кто недавно кухню делал Обещают одно а по факту другое То ДСП сыпется Короче, нашел наконец нормальную контору — заказать кухню с доставкой Сделали за три недели как обещали В общем, смотрите сами по ссылке — кухни от производителя спб недорого и качественно [url=https://kuhni-spb-nbg.ru]https://kuhni-spb-nbg.ru[/url] Не ведитесь на салоны-прокладки с наценкой 200% Сам полгода выбирал теперь знаю

  1937. CaryDap

    Honest assessment is that this is one of the better short reads I have had this week, and a look at siriussuperb reinforced that, the bar for short content is low because most of it sacrifices substance for brevity but this site manages both at once which is harder than it sounds for most writers attempting it.

  1938. Eugenekab

    Quietly the post solved something I had been turning over without quite knowing how to phrase the question, and a look at stashswan extended that quiet solving, content that addresses unformulated needs is content with reader insight and this site has demonstrated that insight at a high rate across the pieces I have read recently.

  1939. Estevancit

    Liked the natural conversational tone throughout, never stiff and never overly casual either, and a stop at snippetvamp kept that comfortable middle ground going, finding a tone that respects the reader without becoming distant or overly familiar is harder than it sounds and this site nails that balance consistently across many different pieces.

  1941. Keatonicecy

    Compared to the usual results for this kind of search this site stands well above the average, and a quick visit to globeflame kept the standard high, you can tell within seconds whether a site is going to waste your time or actually deliver and this one clearly delivers without any false starts.

  1942. Bobbyten

    Reading this with my morning coffee turned into reading the related posts with my morning coffee, and a stop at jovigrove stretched the morning further, content that pulls breakfast into a reading session rather than just accompanying it is content that has earned a higher claim on my attention than the average article does.

  1943. TylerKak

    In 2026 the top providers featured at Vavada are the studios shaping igaming quality. Live dealer rooms are streamed in high definition with professional croupiers. Verification is quick and the payout process usually takes only a few hours. Deposits and withdrawals are available through cards, e-wallets and cryptocurrencies. Loyalty levels unlock better rewards the longer a player stays active. Everything you need to get started is on this site.

  1944. Bartswike

    Quietly the writers approach to the topic differs from the dominant takes I have been encountering, and a stop at haleforge extended that distinctive approach, content that maintains a different perspective without explicitly arguing against the dominant ones is content with confident editorial identity and this site has that confidence throughout pieces.

  1945. KalebOxita

    Glad I stumbled across this post, the explanations actually make sense without needing background knowledge to follow along, and after a stop at herongait the same was true there, no assumptions about the reader just clear writing that anyone can understand from the first line right through to the end.

  1946. ThomasScasy

    A quiet kind of confidence runs through the writing, and a look at hanrim carried that same understated assurance, confidence without bragging is the most attractive register for online writing and the writers here have clearly developed it through practice rather than affecting it through stylistic tricks that would feel hollow eventually.

  1947. Ignaciomouff

    Now planning to recommend this site in a context where my recommendations are taken seriously, and a stop at khakifrost confirmed I should make that recommendation soon, the small but real act of recommending content into spaces where my taste matters is something I take seriously and this site is worth the recommendation.

  1950. AxelShede

    Will be sharing this with a couple of people who care about the topic, and a stop at grecofinch added more material worth passing along, the kind of site that is generous with quality content and does not make you jump through hoops to access it which is appreciated more than the team probably realises.

  1951. Dannyalina

    I came here looking for a quick answer and ended up reading the whole post because it was actually interesting, and after flumelake I had a much fuller picture, no stress and no confusion just a clear walk through the topic that made everything fall into place without much effort.

  1952. Juliomow

    A genuinely unexpected highlight of my reading week, and a look at suntansage extended that pattern, the surprise of finding excellent content rather than the predictable mediocre is one of the few real pleasures of casual web browsing and this site delivered that surprise cleanly today which I really do appreciate.

  1953. Thomaspum

    Found this through a friend who recommended it and now I see why, and a look at tasselskein only strengthened that recommendation in my own mind, word of mouth still works for content that actually delivers and this site is clearly earning recommendations the old fashioned way through quality rather than marketing.

  1955. JeremiahExpix

    More substantial than most of what I find searching for this topic online, and a stop at galagull kept that quality consistent, this is one of those sites where the writing actually rewards careful reading rather than punishing the patient reader with empty filler stretched out across long paragraphs that say very little.

  1956. Milosnums

    Honestly impressed by how much useful content sits in such a small post, and a stop at stereotarot confirmed the rest of the site packs a similar punch, density without confusion is a hard balance to strike and this site has clearly cracked the code on it across many different topic areas covered.

  1957. Dallasroago

    Better than most of the writing I have come across on this topic recently, simpler and more direct, and a look at crystalcovemerchantgallery continued in that same way, a real outlier in a crowded space full of repetitive content that says little while taking up a lot of reader time today which is unfortunate.

  1960. Jaceculge

    Came in for one specific question and got answers to three I had not even thought to ask, and a look at julyelm extended that bonus value pattern, the kind of resource that anticipates reader needs rather than just answering the literal question asked is the gold standard and this site reaches it.

  1961. EmanuelNub

    Granted I am giving this site more credit than I usually give new finds, and a look at senatetrench continued earning that credit, the calibration of how much trust to extend after limited exposure is something I do carefully and this site has earned more trust on shorter exposure than most due to consistent quality across.

  1962. Jaxonmab

    Glad I gave this fifteen minutes rather than the usual three minute skim, and a look at glyphfig earned the same investment, time spent on quality content is rarely wasted but the reverse is also true and learning which sites deserve which kind of attention is part of being a careful online reader.

  1964. JustinKer

    Took a quick scan first and then went back to read properly because the post deserved it, and a stop at stencilslick kept me reading carefully too, the kind of writing that earns a slower second pass rather than getting skimmed and forgotten is something I value highly when I happen to find it.

  1965. ElliotDib

    Glad I gave this a chance rather than scrolling past, and a stop at tealsilver confirmed I made the right call, sometimes the best content is hidden behind unassuming headlines that do not scream for attention and learning to slow down and check those out has paid off many times now across years of reading.

  1966. ChristianClunk

    Honestly the simplicity is what makes this work, the topic is not buried under filler words or overly complex examples, and a quick look at timberverge showed the same sensible style, I left with what I came for and no headache from over reading which is a real win these days.

  1967. MarshallFut

    Closed the laptop after this and let the ideas settle for a few hours, and a stop at uptonshade similarly rewarded reflective time, content that benefits from sitting with rather than racing past is the kind I want more of and the kind that this site appears to consistently produce week after week here.

  1968. HughGlund

    Reading this as part of my evening winding down routine fit perfectly, and a stop at tarotshire extended the wind down nicely, content that calms rather than agitates is what I want at the end of the day and this site provides that calming reading experience reliably which is increasingly rare across the modern web.

  1970. RandallErorp

    However casually I came to this site I have ended up reading carefully, and a look at grecoglobe continued earning that careful reading, the conversion from casual visitor to careful reader is something content earns rather than demands and this site has accomplished that conversion for me over the course of just a few pieces.

  1971. LowellCax

    Just want to flag that this was useful and not bury the appreciation in caveats, and a look at fluxhusk earned the same direct praise, recognising good work without hedging it with criticism is something I try to practice because over qualified compliments tend to read as backhanded and miss the point sometimes.

  1972. AlonzoMaL

    Felt like I was reading something written by someone who actually thinks about the topic rather than reciting it, and a look at herongrip reinforced that impression, the difference between recited content and considered content is huge and this site clearly belongs to the latter category which I appreciate as a careful reader looking for substance.

  1973. pereplanirovka kvartir_rqsr

    Слушайте кто с ремонтом Затеял ремонт в хрущёвке Мосжилинспекция завернёт любые работы Я уже намучился Короче, единственное что реально работает — услуги по согласованию перепланировки без проблем И в инспекцию подадут В общем, вся инфа вот здесь — перепланировка квартир [url=https://pereplanirovka-kvartir-ksd.ru]перепланировка квартир[/url] Не тяните Перешлите тому кто затеял ремонт

  1974. HarleyQuadE

    A piece that suggested careful editing without showing the marks of the editing, and a look at udonvivid continued that invisible polish, the best editing disappears into the prose and this site reads as having been edited with skill that does not announce itself which is the highest compliment I can offer any blog content.

  1976. Laneden

    Bookmark folder reorganised slightly to make this site easier to find, and a look at jumbohelm earned the same accessibility upgrade, the small organisational moves I make for sites I expect to return to often are themselves a signal of how much I trust them and this site triggered those moves naturally.

  1977. pereplanirovka kvartir_cuMr

    Слушайте кто ремонт затеял Решил санузел немного расширить А тут оказывается столько бумаг Я уже голову сломал Короче, нашел наконец нормальных специалистов — услуги по перепланировке квартир под ключ Всё за месяц закрыли В общем, смотрите сами по ссылке — перепланировка квартир [url=https://pereplanirovka-kvartir-owy.ru]перепланировка квартир[/url] Не начинайте без проекта Перешлите тому кто тоже ремонт затеял

  1978. KyrieCaupe

    During my morning reading slot this fit perfectly into the routine, and a look at hazmug extended that perfect fit into the rest of the routine, content that matches the rhythm of how I actually read rather than demanding accommodation from my schedule is content well calibrated to its likely audience and this site has it.

  1979. Prestonheilm

    Skipped the comments to avoid spoilers and came back later to find them genuinely worth reading, and a stop at turbansample extended that surprised respect, when the discussion below a post matches the quality of the post itself you have found something special and this site appears to attract that kind of audience.

  1980. Diegocam

    Felt the post had been quietly polished rather than aggressively styled, and a look at driftorchardmerchantgallery confirmed the same understated polish, sites whose quality reveals itself slowly rather than announcing itself loudly are the kind I trust more deeply because the trust is not based on first impressions of marketing but actual substance.

  1981. JosephloB

    Once I trust a site this much I tend to read everything they publish and that is the trajectory I am on with this one, and a stop at galeember confirmed the trajectory, the rare progression from interested reader to comprehensive reader is something only certain sites earn and this one is earning that progression rapidly.

  1983. BradenscurA

    Grateful for posts like this one, they remind me there are still places online run by people who care about quality, and a look at gnarfrost reflected the same standards, you can tell the difference between content made for readers and content made just for search engines today and this is the former.

  1986. Leonardpriem

    Reading this on a difficult day was a small bright spot, and a stop at syruptunic extended that brightness, content that improves a hard day is content that has earned a particular kind of place in my reading habits and this site is occupying that uplifting role for me today which I appreciate clearly.

  1987. JosiahDiz

    Worth recognising the specific care that went into how this post ended, and a look at seriftackle maintained the same careful conclusions, endings are where most blog content falls apart and this site has clearly invested in the closing stretches of its pieces rather than letting them simply trail off when energy fades.

  1988. CraigTuh

    Just want to say thank you for putting this together, posts like these make searching online actually worth it sometimes, and a quick look at khakikite kept that going, useful and easy to read without any of the tricks that ruin most blog comment sections lately on the wider open web.

  1989. Destinkit

    Excellent execution from start to finish, the post never loses its rhythm and the points stay sharp, and a quick stop at sectorsatin kept the same level going, consistency like this across a site is the marker of a serious operation rather than a casual side project running on autopilot somewhere else.

  1990. Amaripup

    Looking through other posts here the consistency is what makes the site valuable rather than any single piece, and a stop at trancetidal extended that consistency observation, sites whose value lies in the ongoing pattern rather than in standout posts are sites I trust more deeply and this one has clearly built that kind of trust.

  1991. JeremyCek

    Honest assessment after reading this twice is that it holds up under careful attention, and a look at snoozestaple extended that durability across more pages, content that survives a second read without revealing weak spots is rarer than the average reader probably realises and this site clearly cleared that bar.

  1992. Jamarcussnuch

    Felt a small spark of recognition when the post named something I had been struggling to articulate, and a look at havenfoam produced more such moments, the rare service of giving readers language for fuzzy intuitions is one of the higher values that good writing can provide and this site offered several today instances.

  1996. Rexmeeks

    Reading this on the train into work was a better use of the commute than my usual choices, and a stop at gridivory extended that commute reading well, content that improves transit time rather than just filling it is content with practical benefit and this site has earned its place in my morning commute reading rotation.

  1997. Saulhop

    Thanks for the readable length, I finished it without checking how much was left, and a stop at foamhull kept me reading the same way, when I stop noticing the length of a piece because the content is engaging enough to sustain attention without willpower the writer has done their job well today.

  2000. WayneFep

    Closed three other tabs to focus on this one and never opened them again, and a stop at vetovarsity similarly held attention exclusively, content that crowds out other reading from working memory is content with real density and this site has demonstrated that density across multiple pages I have visited so far this morning.

  2001. Ianblunc

    A slim post with substantial content per word, and a look at vincasinger maintained the same density, the content per word ratio is something I track informally and this site scores high on that ratio compared to most sources I read regularly which is a quiet indicator of careful editorial work behind the scenes.

  2003. ErvinBit

    Honest reaction is that I want to send this to a friend who would benefit from it, and a look at twainsilica added more material I will pass along too, the impulse to share is the strongest signal I have for content quality and this site is generating that impulse cleanly across multiple posts.

  2004. Damionnem

    The structure of the post made it easy to follow without losing track of where I was, and a look at heronhilt kept the same logical flow going, this site clearly understands that organisation is half the battle in keeping readers engaged from the first line to the last across any kind of post.

  2005. JoelHedly

    Glad to find a site whose links lead somewhere worth going rather than back to itself for SEO juice, and a stop at tarmacstork kept that generous outbound feel, citing other peoples work with real respect rather than just for ranking signals is a sign of an honest operation worth supporting going forward.

  2006. Germansal

    Loved the writing voice here, friendly without being fake and confident without being arrogant, and a stop at dunemeadowcommercegallery carried the same tone forward, the kind of personality that makes a reader feel welcome rather than lectured at which is a balance plenty of writers struggle to find no matter how long they have been at it.

  2007. Vaughnbef

    Liked the balance between depth and brevity, never too shallow and never too long, and a stop at gnarkit kept the same balance going across the rest of the site, this is one of the harder skills in writing and the team here clearly has it figured out very well indeed across every page.

  2009. HowardChito

    Once you start reading carefully here it is hard to go back to lower quality alternatives, and a stop at galehelm reinforced that ratchet effect, the way good content raises standards is real over time and this site has clearly contributed to raising my expectations for what is possible in writing on the topic generally.

  2010. LawrenceProts

    Appreciated that the writer trusted the reader to follow along without constant restating of earlier points, and a look at junipercovemerchantgallery continued that respect for the reader, treating an audience as capable adults rather than as people to be hand held through every paragraph is something I notice and value highly across the open internet today.

  2011. Jackwairl

    Now adding a small note in my reading log that this site is one to watch, and a look at slacktally reinforced the watch status, the few sites I track deliberately rather than encounter accidentally are sites I expect ongoing returns from and this one has cleared the bar for that elevated tracking based on what I read.

  2013. CordellAgofe

    A piece that prompted a small mental rearrangement of how I order related ideas, and a look at hekarc extended that rearranging effect, content that affects the structure of my thinking rather than just adding to it is content with the deepest kind of impact and this site is reaching that depth for me today.

  2014. Konnorfat

    Skipped lunch to finish reading, which says something, and a stop at shoreviper kept me at my desk longer than planned, when content beats the lunch impulse the writer has done something genuinely impressive in an attention environment full of immediately satisfying alternatives competing for the same finite block of reader time.

  2015. ClydeIdeap

    Now noticing the careful balance the post struck between confidence and humility, and a stop at smeltstraw maintained the same balance, finding the line between asserting and admitting is hard and this site has clearly developed the calibration to walk that line consistently which produces a more persuasive reading experience for me.

  2017. Marlonker

    Will be coming back to this for sure, too much good content to absorb in one sitting, and a stop at vikingturban only added more pages I want to dig through, this site is going onto my regular rotation list because it consistently delivers something worth the visit lately rather than empty filler.

  2018. Corypat

    Felt the writer respected the topic without being precious about it, and a look at tomatotactic continued that respectful but unfussy treatment, finding the right register for serious topics is hard and this site has clearly figured out how to take the topic seriously while still being readable for casual visitors regularly.

  2019. JonathanScero

    Quality work here, the post reads cleanly and the points stay focused throughout, and a stop at grifffume kept the standard high, you can tell the writer cares about the final result rather than just hitting publish for the sake of having something new on the page to feed the search engines.

  2020. Bryanjaf

    Started this morning and finished at lunch with a small sense of having spent the time well, and a look at foilfrost extended that satisfaction into the afternoon, content that fits naturally into the rhythm of a working day rather than demanding a dedicated reading block is increasingly the kind I prefer.

  2022. CoryKeype

    Now I want to find more sites like this but I suspect they are rare, and a look at superbtundra extended that thought, the few sites that meet this quality bar are precious specifically because they are rare and finding others like them is one of the ongoing projects of careful internet curation across the years.

  2023. BrettJaics

    A memorable post for me on a topic I had thought I was tired of, and a look at kitidle suggested the same site can refresh other tired topics, sites that can revive my interest in subjects I had written off as exhausted are doing rare work and this one is clearly doing that for me today.

  2026. 1xbet apk_naKr

    Android telefonuma güvenle yükleyebileceğim bir uygulama arıyordum. Play Store’da resmi uygulamayı bulamayınca çok hayal kırıklığı yaşadım. Adımları doğru sırayla uyguladıktan sonra erişim sorunsuz açıldı. En sonunda sağlam bir adrese ulaştım ve size de tüm detayları aktarmak istedim, güncel bilgilere buradan bakabilirsiniz: 1xbet android uygulama [url=https://1xbet-apk-10.com]1xbet android uygulama[/url]. Valla bak net söyleyeyim — mobil versiyonu her şeyi thinkmüş resmen.

    Hiçbir güvenlik sorunu yaşamadım yükleme esnasında. Kendi deneyimlerimi aktarıyorum size — en güvenilir uygulama bu oldu artık. Şimdiden iyi şanslar ve bol kazançlar…

  2027. Borisnuh

    A particular pleasure to read this with a fresh coffee, and a look at surgetarmac extended the pleasure across more pages, content that pairs well with quiet morning rituals is something I have come to value highly and this site has the kind of energy that fits naturally into a calm reading routine.

  2028. proekt pereplanirovki kvartiri_eeMt

    Народ всем привет Замучился я уже с этим согласованием Оказывается без бумажки ты никто Я уже голову сломал Короче, единственные кто делает быстро — проект перепланировки квартиры под ключ И техзаключение сделали В общем, сохраняйте себе — сделать проект перепланировки квартиры в москве [url=https://proekt-pereplanirovki-kvartiry-hmf.ru]https://proekt-pereplanirovki-kvartiry-hmf.ru[/url] Потом себе дороже Перешлите тому кто ремонт затеял

  2029. BarneyKep

    Started thinking about my own writing differently after reading, and a look at echoharborcommercegallery continued that reflective effect, content that influences how I work rather than just informing what I know is content with the highest kind of impact and this site has triggered some of that reflective influence today on me.

  2030. shkola onlain_kyOl

    Слушайте кто перевёл на дистант Учителя бесят своими требованиями А ещё эти поборы в классе Нервов потратил немерено Короче, единственная школа где реально учат — школа онлайн с аттестатом государственного образца Ребёнок занимается дома без нервов В общем, сохраняйте себе — лбс это [url=https://shkola-onlajn-krt.ru]лбс это[/url] Не мучайте детей Перешлите другим родителям кто устал от школы

  2031. FranklinAbicy

    Now setting this aside as a model of how to write thoughtfully on the topic, and a stop at sodasalt extended that model status, content that becomes a reference for how a kind of writing should be done is content with influence beyond its own readership and this site is reaching that level for me clearly today.

  2033. Rodneysix

    Reading this on the train into work was a better use of the commute than my usual choices, and a stop at slippersixth extended that commute reading well, content that improves transit time rather than just filling it is content with practical benefit and this site has earned its place in my morning commute reading rotation.

  2034. JimmyQuoca

    Decided after reading this that I would check this site weekly going forward, and a stop at heronjoust reinforced that commitment, deciding to add a site to a regular rotation requires meeting a quality bar that very few places clear and this one cleared it cleanly without any noticeable effort or marketing push behind it.

  2036. Chadtyday

    If you scroll past this site without looking carefully you will miss something, and a stop at hazegloss extended that mild warning, the surface of the site does not advertise its quality loudly which means careful attention is required to recognise what is being offered here which is itself a kind of editorial signal.

  2037. pereplanirovka kvartir_ygsr

    Народ всем привет Решил снести стену между комнатами А тут оказывается бумажек этих Я уже намучился Короче, единственное что реально работает — услуги по перепланировке квартир под ключ И чертежи сделают В общем, сохраняйте себе — услуги по согласованию перепланировки [url=https://pereplanirovka-kvartir-ksd.ru]услуги по согласованию перепланировки[/url] Потом штраф и суды Перешлите тому кто затеял ремонт

  2038. AlfredVof

    Honestly this kind of writing is why I still bother to read independent sites, and a look at tinklesaddle extended that broader reflection, the few sites that justify continued attention to non algorithmic content are sites like this one and finding them periodically is enough to keep my reading habits oriented toward independent rather than aggregated content.

  2039. Alfredmot

    Now adding the homepage to my regular check rotation rather than waiting for individual links to find me, and a stop at groovehale confirmed the rotation upgrade, the move from passive discovery to active checking is a vote of confidence in a sites ongoing quality and this site has earned that active engagement clearly.

  2040. Benwah

    Bookmark added in three places to make sure I do not lose the link, and a look at taigascenic got the same redundant treatment, sites I am afraid to lose are the rare keepers and this is clearly one of them based on what I have read so far across this and a couple of related posts.

  2042. Phillippsync

    Reading this in the morning set a good tone for the day, and a quick visit to lavenderharborcommercegallery kept that good tone going, content can do that sometimes when it hits the right notes and finding sites that consistently strike that tone is something I have learned to recognise and reward with regular visits.

  2043. JadonGoava

    Reading this in three sittings because the day was fragmented, and the piece survived the fragmentation, and a stop at unionstaff held up under similar reading conditions, content engineered for continuous attention is fragile in modern conditions and this site reads as durable across the realistic ways people consume content today.

  2044. JermaineTox

    Honest take is that this was better than I expected when I clicked through, and a look at tundrastout reinforced that, the bar for online content has dropped so much that finding something thoughtful and well constructed feels almost noteworthy now which says more about the average than about this site itself.

  2045. Baronadvaw

    Honest reaction is that this is the kind of writing I would defend in a conversation about good blog content, and a look at heyaro reinforced that, the rare site whose work I would actively recommend rather than just tolerate is the kind I want to support through return visits regularly.

  2046. Ericlooge

    Worth marking this site as one to come back to deliberately rather than by accident, and a stop at tundraturtle reinforced that intention, the difference between sites I find again by chance and sites I return to on purpose is meaningful and this one has clearly moved into the deliberate return category for me.

  2047. SaulNic

    Decided to subscribe to the RSS feed if there is one, and a stop at salemsolid confirmed that decision, content that I want delivered to me proactively rather than just remembered when I have time is content that has earned a higher level of commitment from me as a reader looking for reliable sources.

  2048. GeneCaX

    Honest take is that this was better than I expected when I clicked through, and a look at shorevolume reinforced that, the bar for online content has dropped so much that finding something thoughtful and well constructed feels almost noteworthy now which says more about the average than about this site itself.

  2050. RexFlusa

    The use of plain language without dumbing down the topic was really well done, and a look at turtleudon continued in that same accessible style, this is something many technical writers fail at because they either confuse their readers or condescend to them but here neither problem appears at all which is impressive really.

  2051. MiltonPaush

    Big thanks to whoever wrote this, you saved me a lot of time hunting for the same info on other sites, and a stop at waveharbormerchantgallery only added more useful detail without going off topic, that kind of focus is honestly hard to come across these days when most posts wander everywhere.

  2052. KellyExerb

    Honestly impressed by the consistency of voice across what I have read so far, and a quick visit to elmharbormerchantgallery continued that consistent feel, when a site reads like one careful person rather than a committee the experience is more rewarding for the reader who notices these subtle editorial details over time.

  2056. Damionevine

    Worth saying that the quiet confidence of the writing is what landed first, and a look at studiosalute continued that quiet quality, confident writing without the loud display of confidence is a rare combination and this site has clearly developed both the knowledge and the editorial restraint to land that combination consistently.

  2057. NicholasWes

    Really appreciate that the writer did not overstate the importance of the topic to make the post feel weightier, and a quick visit to knollgull maintained the same modest framing, content that is honest about its own scope rather than inflating itself is the kind I trust and return to repeatedly over time.

  2059. Matttwida

    Adding to the bookmarks now before I forget, that is how good this is, and a look at hickorygrid confirmed the rest of the site is worth saving too, this is one of those rare finds that justifies the time spent searching the web for once which is a relief in the current environment.

  2060. Kimcox

    Really appreciate that the writer did not overstate the importance of the topic to make the post feel weightier, and a quick visit to vinyltrophy maintained the same modest framing, content that is honest about its own scope rather than inflating itself is the kind I trust and return to repeatedly over time.

  2062. KentonKerly

    Generally my attention drifts on long posts but this one held it through the end, and a stop at vectortimber earned the same sustained focus, content that defeats my drift tendency is content with substantive pulling power and this site has demonstrated that pulling power across multiple pieces in a session that has now run quite long actually.

  2063. Connorenese

    Reading this felt productive in a way most internet reading does not, and a look at glyjay continued that productive feeling, sometimes the open web feels like a waste of time but sites like this remind me why I still bother to look around rather than retreating to old reliable sources for everything I need.

  2064. Harryraw

    Reading this prompted me to clean up some old notes related to the topic, and a stop at shadetassel extended that organising urge, content that triggers personal organisation rather than just consuming attention is content with motivating energy and this site has the kind of clarity that prompts active follow up rather than passive consumption.

  2065. VanceZed

    Started thinking about my own writing differently after reading, and a look at tildeserene continued that reflective effect, content that influences how I work rather than just informing what I know is content with the highest kind of impact and this site has triggered some of that reflective influence today on me.

  2066. Dillondag

    Glad to have another data point on a question I am still thinking through, and a look at vortexvandal added two more, content that acknowledges its place in a wider conversation rather than pretending to settle the question alone is intellectually honest in a way that I wish was more common across the open web.

  2067. DravenBuife

    A piece that respected the reader by not over explaining the obvious, and a look at moonharborcommercegallery continued that calibrated approach, finding the right level of explanation is one of the harder editorial calls and this site has clearly thought carefully about what readers will already know versus what they need help with consistently.

  2068. BobCog

    Pass this along to colleagues if the topic comes up, the framing here is sensible, and a stop at crecall adds more useful angles to share, the kind of content that improves conversations rather than just feeding them is what makes a resource genuinely valuable in professional contexts going forward over time and across project boundaries too.

  2069. VanceObelf

    Solid post, the structure is easy to follow and the language stays simple even when the topic gets a bit more involved, and a look at elmwoodcommercegallery kept that same standard going, so I left feeling like the time spent here was actually worth something for once which is rare lately.

  2070. Mateonon

    A piece that was confident enough to leave some questions open rather than forcing closure, and a look at timbertrailmerchantgallery continued that intellectual honesty, content that admits the limits of its scope is more trustworthy than content that pretends to total understanding and this site has the right calibration on certainty consistently.

  2071. LarryMassy

    Genuinely useful read, the points are practical and easy to apply right away, and a quick look at woodcovemerchantgallery confirmed that this site is consistent in that approach, looking forward to digging through the rest of it when I get the chance to sit down properly later in the week or this weekend.

  2072. Fredfrero

    Approaching this with the usual skepticism I bring to new sites and being slowly persuaded, and a stop at daisyharborcommercegallery continued that gradual persuasion, the careful path from skeptical reader to genuine fan is the only one I trust and this site has walked me along that path through patient consistent quality across pieces.

  2073. PeteGer

    Picked this up while looking for something else and ended up reading every paragraph because it was actually informative, and after hoxfix I was sure I would come back, that does not happen often when most sites bury the useful parts under endless ads and pop ups today and across most categories online.

  2075. DeanGycle

    Glad I clicked through from where I did because this turned out to be worth the time spent, and after hazeherb I had a fuller picture, the kind of content that earns its visitors through delivering value rather than chasing them through aggressive advertising or constant pop ups appearing everywhere on the screen lately.

  2078. shkola onlain_vfOn

    Слушайте кто ищет нормальную школу Дневники эти вечные А знаний реальных ноль Короче, реально крутая система — школы дистанционного обучения с индивидуальным подходом Аттестат государственный В общем, сохраняйте себе — уроки онлайн [url=https://shkola-onlajn-vem.ru]https://shkola-onlajn-vem.ru[/url] Переходите на нормальное обучение Перешлите другим родителям

  2079. RayfordVof

    Заправка для картриджей Используемая нами заправка для картриджей гарантирует отсутствие пыли и протечек тонера внутри вашего аппарата. Мы соблюдаем все технологические стандарты производителей оргтехники.

  2080. Mauricevup

    Without overstating it this is a quietly excellent post, and a look at simbasienna extended that quiet excellence, content that earns superlatives without demanding them through marketing language is content that has truly earned them through the substance and this site has clearly produced work in that earned excellence category today.

  2084. proekt pereplanirovki kvartiri_rlMt

    Народ всем привет Хочу снести стену между кухней и комнатой Оказывается без бумажки ты никто Я уже голову сломал Короче, единственные кто делает быстро — проект перепланировки квартиры в Москве с гарантией И чертежи нарисовали В общем, вся инфа вот здесь — сделать проект перепланировки квартиры в москве [url=https://proekt-pereplanirovki-kvartiry-hmf.ru]https://proekt-pereplanirovki-kvartiry-hmf.ru[/url] Не начинайте без проекта Перешлите тому кто ремонт затеял

  2085. Lincolnfooth

    Decided this was the kind of site I would defend in a discussion about good blog content, and a stop at koalaglade reinforced that, very few sites earn active defence rather than passive consumption and this one has clearly crossed that threshold for me without needing any explicit pitch from the writers themselves either.

  2086. shkola onlain_baOl

    Слушайте кто перевёл на дистант Задолбала эта обычная школа А качество знаний при этом никакое Я уже голову сломал Короче, единственная школа где реально учат — школа онлайн с аттестатом государственного образца Аттестат государственный — не хуже обычного В общем, жмите чтобы не потерять — лбс это [url=https://shkola-onlajn-krt.ru]лбс это[/url] Не мучайте детей Перешлите другим родителям кто устал от школы

  2087. AbrahamDeevy

    Now noticing that the post never raised its voice even when making a strong point, and a look at solacevelour continued that calm volume, content that can make important points without resorting to typographic emphasis or emotional appeal is content that trusts its substance to do the work and this site has that confidence consistently.

  2088. NoahSpoom

    Pleasant surprise, the post delivered more than the headline promised, and a stop at hiltgable continued that pattern of under promising and over delivering, the rarest combination on the modern web where most content does the opposite by promising the world and delivering thin recycled summaries instead each time you click on something interesting.

  2089. Mateonon

    Following a few of the internal links revealed more posts of similar quality, and a stop at timbertrailmerchantgallery added more to that growing pile, sites where internal links lead to more good content rather than to more of the same recycled material are sites with depth and this one has clearly built that depth carefully.

  2090. GeneCaX

    Recommended without reservation for anyone interested in the topic at any level of expertise, and a look at shorevolume only strengthens that recommendation, this site clearly knows how to serve readers across a range of backgrounds without watering down the content or talking past anyone in the audience which is genuinely impressive to see.

  2091. MiltonPaush

    Reading this in a moment of low energy still kept my attention, and a stop at waveharbormerchantgallery continued that engagement under suboptimal conditions, content that survives the reader being tired is content with extra reserves of pull and this site has the kind of writing that holds up even when I am not at my reading best.

  2092. Jeremiahskers

    A piece that read as if the writer was thinking carefully rather than just typing fluently, and a look at skiffvantage continued that considered quality, the difference between fluent typing and careful thinking shows up in writing and this site reads as the product of thought rather than just the product of language fluency apparently.

  2093. Connorenese

    Reading this felt productive in a way most internet reading does not, and a look at glyjay continued that productive feeling, sometimes the open web feels like a waste of time but sites like this remind me why I still bother to look around rather than retreating to old reliable sources for everything I need.

  2094. Fredfrero

    Looking for similar voices elsewhere has come up empty in my recent searches, and a stop at daisyharborcommercegallery extended the search frustration, the rare site that does what no other does in quite the same way is precious and this one has clearly developed a particular approach that I have not been able to find duplicates of.

  2095. Lowelldew

    Top notch writing, every paragraph carries weight and nothing feels like filler, and a stop at shoretunic reflected that same care, a rare thing on the open web these days where most pages exist for clicks rather than actual reader value or anything close to that which is honestly a real shame.

  2096. Troyhem

    A piece that read as the work of someone who reads carefully themselves, and a look at sloganturban continued that informed feel, writers who are also serious readers produce work with a different quality and this site reads as the product of someone steeped in good writing rather than just generating content for an audience.

  2097. RobinTerty

    Worth recognising that the post handled a familiar topic without reaching for any of the obvious hot takes, and a stop at embermeadowmerchantgallery continued that fresh treatment, sites that find new angles on subjects others have exhausted are sites worth following carefully and this one has clearly developed that exploratory instinct through patient practice.

  2098. EzekielDourO

    Quality work here, the post reads cleanly and the points stay focused throughout, and a stop at trumpetsixth kept the standard high, you can tell the writer cares about the final result rather than just hitting publish for the sake of having something new on the page to feed the search engines.

  2099. LeoVes

    Comfortable reading experience throughout, no jarring tone shifts and no awkward formatting, and a look at vinylvessel kept that smooth feel going, the kind of editorial polish that goes unnoticed when present but glaring when absent is something this site has clearly invested in across the broader content as well which deserves recognition.

  2101. JamesFouct

    Now leaving a small mental note to recommend this when the topic comes up in conversation, and a look at fiabush extended that recommend ready feeling, content that arms me with shareable references for likely future conversations is content with social value and this site is providing that conversational ammunition consistently for me lately.

  2102. Edwinsnaft

    More substantial than most of what I find searching for this topic online, and a stop at mossharborcommercegallery kept that quality consistent, this is one of those sites where the writing actually rewards careful reading rather than punishing the patient reader with empty filler stretched out across long paragraphs that say very little.

  2107. Ernestohib

    Skipped a meeting reminder to finish the post, and a stop at saddleswamp held me past another reminder, when content beats meetings the writer is doing something extraordinary because meetings have institutional support behind them and yet good writing can still occasionally win that competition for attention which I find heartening today.

  2108. Anthonyten

    Honest take is that this was better than I expected when I clicked through, and a look at hoxhem reinforced that, the bar for online content has dropped so much that finding something thoughtful and well constructed feels almost noteworthy now which says more about the average than about this site itself.

  2109. pereplanirovka kvartir_rjsr

    Слушайте кто с ремонтом Затеял ремонт в хрущёвке Мосжилинспекция завернёт любые работы Потратил кучу времени Короче, единственное что реально работает — перепланировка квартиры в Москве с гарантией И в инспекцию подадут В общем, жмите чтобы не потерять — перепланировка помещения [url=https://pereplanirovka-kvartir-ksd.ru]https://pereplanirovka-kvartir-ksd.ru[/url] Не тяните Перешлите тому кто затеял ремонт

  2110. Mateonon

    Liked everything about the experience, from the opening through to the closing notes, and a stop at timbertrailmerchantgallery extended that into more pages, finding a site where the editorial vision shows through every choice rather than feeling random is an increasingly rare experience and one I am glad to have today during this particular reading session.

  2111. AbrahamDeevy

    Once you start reading carefully here it is hard to go back to lower quality alternatives, and a stop at solacevelour reinforced that ratchet effect, the way good content raises standards is real over time and this site has clearly contributed to raising my expectations for what is possible in writing on the topic generally.

  2112. StuartHauch

    Now recognising that the post handled the topic with appropriate technical precision without becoming dry, and a stop at tweedvolume continued that balance, technical precision and readability are often in tension and this site has clearly figured out how to maintain both at once which is one of the harder editorial achievements in the form.

  2113. Emmettweivy

    Really nice to see things explained without overcomplicating the topic, the words flow naturally and stay easy to follow, and a short visit to velvetbrookmerchantgallery only added to that experience because the same simple approach is used across the rest of the page too without any change in tone.

  2114. GeneCaX

    Walked away in a slightly better mood than when I started reading, that says something about the writing, and a stop at shorevolume kept that going, content that leaves you feeling more capable rather than overwhelmed is the kind I keep coming back to again and again over the years and across many topics.

  2115. Mathewnek

    Over the course of reading several posts here a pattern of quality has emerged, and a stop at arobell confirmed the pattern, the difference between sites that hit quality occasionally and sites that hit it consistently is huge and this site has clearly demonstrated the consistent kind through what I have read this morning.

  2116. ToddNot

    Now feeling confident that this site will continue producing work I will want to read, and a look at hiltgem extended that confidence into the future, projecting forward from current quality to expected future quality is something I do for sites I genuinely follow and this one has earned that forward looking trust clearly today.

  2117. QuentinSkype

    Well done, the writing is professional without being stiff, and the topic is treated with care, and a look at frostridgemerchantgallery reflected that approach, the kind of site I would point a colleague to if they asked for a reliable starting point on this topic in the future without any hesitation at all.

  2118. Malcolmblulk

    Now adjusting my expectations upward for the topic based on this post, and a stop at kraftgroove continued that bar raising effect, content that resets what I think is possible on a subject is doing real work in shaping my standards and this site is providing those bar raising experiences at a notable rate during sessions.

  2119. Fredfrero

    A particular pleasure to read this with a fresh coffee, and a look at daisyharborcommercegallery extended the pleasure across more pages, content that pairs well with quiet morning rituals is something I have come to value highly and this site has the kind of energy that fits naturally into a calm reading routine.

  2120. MalcolmSax

    Looking at this objectively the editorial quality is hard to deny even setting aside personal taste, and a stop at nyxsip maintained the same objective quality, the gap between what I personally enjoy and what is objectively well crafted exists and this site clears both bars simultaneously which is rarer than it sounds.

  2121. Connorenese

    Reading this on a long flight and finding it the best thing I read across hours of trying, and a stop at glyjay kept the streak going, when content beats long flight reading you know it has substance because flight reading is a hard test of a piece given the alternatives available everywhere.

  2122. MiltonPaush

    Liked how the post handled an objection I was forming as I read, and a stop at waveharbormerchantgallery similarly anticipated where my thinking was going next, the rare writer who can predict reader concerns and address them in advance is doing something most online content fails to do despite that being basic editorial work.

  2123. WendellStubs

    Skipped a meeting reminder to finish the post, and a stop at heathfoam held me past another reminder, when content beats meetings the writer is doing something extraordinary because meetings have institutional support behind them and yet good writing can still occasionally win that competition for attention which I find heartening today.

  2127. JohnCic

    Now thinking I want more sites built on this kind of editorial foundation, and a stop at fribrag extended that wish into a broader hope, sites built on substance and care rather than on metrics and growth are the kind of sites I want to see more of and this one is a small example worth supporting.

  2128. Vaughndauth

    Honestly thank you to whoever wrote this because it scratched an itch I had not quite been able to articulate, and a stop at sweatertorso kept that satisfying feeling going, the kind of writing that meets unspoken needs is special and this site clearly has writers who understand their readers more than most do today.

  2130. Josejek

    Just sat with this for a bit longer than I usually would because the points are worth thinking about, and after nightfallcommercegallery I had even more to chew on, the kind of post that nudges your thinking forward without forcing the issue is something I have always appreciated in good writing online.

  2131. JosephSkevy

    Felt the post had been written without using a single buzzword, and a look at skifftornado continued that clean vocabulary, content free of jargon and trendy phrases reads better and ages better and this site has clearly committed to a vocabulary that will not feel dated in three years which is impressive editorially.

  2132. LeoVes

    Most of the time I bounce off similar pages within seconds, and a stop at vinylvessel held me longer than I would have predicted, the ability to convert a likely bouncing visitor into an engaged reader is a quality signal and this site has demonstrated that conversion ability across multiple visits where I expected to bounce.

  2133. shkola onlain_pnOn

    Народ у кого дети Замучились мы с этой обычной школой А знаний реальных ноль Короче, нашли отличный выход — онлайн школы с зачислением и документами Уроки в комфортное время В общем, вся инфа вот здесь — дистанционное обучение москва [url=https://shkola-onlajn-vem.ru]https://shkola-onlajn-vem.ru[/url] Переходите на нормальное обучение Перешлите другим родителям

  2134. pereplanirovka kvartir_esMr

    Слушайте кто ремонт затеял Хотел стену снести между комнатами Разрешения эти дурацкие Нервов просто не осталось Короче, единственные кто берётся за всё — узаконивание перепланировки без нервотрёпки И чертежи сделали В общем, смотрите сами по ссылке — услуги по перепланировке квартир [url=https://pereplanirovka-kvartir-owy.ru]услуги по перепланировке квартир[/url] Потом себе дороже выйдет Перешлите тому кто тоже ремонт затеял

  2135. Mikemab

    Useful read, especially because the writer did not assume too much background from the reader, and a quick look at violetharbormerchantgallery continued in the same way, a thoughtful site that meets people where they are which is something the modern web could use a lot more of for both casual and serious readers.

  2136. UlyssesBemia

    Useful read, especially because the writer did not assume too much background from the reader, and a quick look at vesseltame continued in the same way, a thoughtful site that meets people where they are which is something the modern web could use a lot more of for both casual and serious readers.

  2137. KurtAculp

    A nicely understated post that does not shout for attention, and a look at hubbeat maintained the same quiet quality, understatement is a stylistic choice that distinguishes serious writing from attention seeking writing and this site has clearly committed to the understated approach as a core editorial value rather than just a phase.

  2138. Dominicabeld

    Reading the writers other posts after this one suggests the quality is consistent rather than peak, and a stop at thatchvista confirmed the consistent quality reading, sites that hold the same level across many pieces rather than peaking on a few are sites with sustainable editorial discipline and this one has clearly developed that.

  2139. JeffreyGex

    Generally I find the content on similar topics frustrating in specific ways and this post avoided all of them, and a look at garnetharborcommercegallery continued that frustration free experience, content that sidesteps the standard failure modes of its genre is content with editorial awareness and this site has clearly studied what fails elsewhere consistently.

  2140. AbelPaine

    Solid value packed into a relatively short post, that takes skill, and a look at siskastencil continues the dense useful content across more pages, this site clearly understands that respecting reader time is itself a form of generosity which is something most blog operations seem to have forgotten lately across the wider open web.

  2142. Lawsonden

    Closed several other tabs to focus on this one as I read, and a stop at hilthive held my undivided attention the same way, content that earns full focus in an attention environment full of competing pulls is content doing something genuinely well and the team behind it deserves recognition for that achievement consistently.

  2143. NoelShify

    Now adjusting my mental model of how the topic fits into the broader landscape, and a look at dawnridgemerchantgallery extended that adjustment, content that affects my structural understanding rather than just my factual knowledge is content with deeper impact and this site is providing those structural updates at a meaningful rate consistently across topics.

  2145. JohnnieKeype

    Going to come back when I have more time to read carefully, the post deserves more than a quick scan, and a stop at violetharborcommercegallery reinforced that, this is the kind of site that rewards a slower read which is hard to find in this fast paced corner of the internet but really worthwhile.

  2147. Mathewnek

    If I were to recommend a starting point for the topic this site would be near the top of my list, and a stop at arobell reinforced that recommendation status, the small list of starting point recommendations I keep for friends asking about topics is short and this site is now firmly on it.

  2148. AlfonsoSox

    Comfortable reading experience throughout, no jarring tone shifts and no awkward formatting, and a look at kraftkale kept that smooth feel going, the kind of editorial polish that goes unnoticed when present but glaring when absent is something this site has clearly invested in across the broader content as well which deserves recognition.

  2149. Prestonvef

    Decided not to comment because the post said what needed saying, and a stop at goaxio continued that complete feel, content that does not invite obvious additions or corrections from readers is content that has been carefully considered and this site appears to consistently produce pieces that satisfy rather than provoke unnecessary follow ups.

  2151. LarryMassy

    Generally my comment to other readers about new sites is to wait and see but for this one I would jump to recommend now, and a look at woodcovemerchantgallery reinforced that early recommendation, the speed at which a site earns my recommendation is itself a quality signal and this one has earned mine quickly clearly.

  2152. KenKeese

    Started thinking about my own writing differently after reading, and a look at tallysmoke continued that reflective effect, content that influences how I work rather than just informing what I know is content with the highest kind of impact and this site has triggered some of that reflective influence today on me.

  2153. JuliusNop

    Decided to set aside time later to read more carefully, and a stop at fylcalm reinforced that decision, content that earns a calendar entry rather than just a passing read is in a different tier altogether and this site is clearly working at that elevated level which I really do appreciate as a reader today.

  2154. shkola onlain_ggEl

    Слушайте кто устал от обычной школы Вечные двойки и тройки в дневнике Нервный как спичка Короче, реально удобный формат — школа онлайн с официальным аттестатом Аттестат как у всех В общем, смотрите сами по ссылке — дистанционное обучение москва [url=https://shkola-onlajn-pqs.ru]https://shkola-onlajn-pqs.ru[/url] Переходите на дистант нормальный Перешлите другим родителям

  2155. Vernonpioke

    Closed it feeling slightly more competent in the topic than I started, and a stop at oliveharborcommercegallery reinforced that competence boost, real learning is rare in casual online reading but it does happen sometimes and this site managed to make it happen for me today which is genuinely worth pausing to acknowledge.

  2156. PatrickPlone

    Started imagining how I would explain the topic to someone else after reading, and a look at studiotrader gave me more material for that imagined explanation, content that improves my own ability to discuss a topic is content that has actually transferred knowledge rather than just decorating my screen for a few minutes.

  2157. proekt pereplanirovki kvartiri_svMt

    Народ всем привет Планирую объединить две комнаты в гостиную Оказывается без бумажки ты никто Потратил уйму времени Короче, единственные кто делает быстро — заказать проект перепланировки квартиры недорого И чертежи нарисовали В общем, сохраняйте себе — проектная организация для перепланировки квартиры [url=https://proekt-pereplanirovki-kvartiry-hmf.ru]https://proekt-pereplanirovki-kvartiry-hmf.ru[/url] Потом себе дороже Перешлите тому кто ремонт затеял

  2158. shkola onlain_piOl

    Слушайте кто перевёл на дистант Ребёнок устаёт в школе как лошадь То ремонт, то экскурсии, то подарки Я уже голову сломал Короче, единственная школа где реально учат — онлайн обучение для детей с любого возраста Уроки в удобное время В общем, жмите чтобы не потерять — лбс это [url=https://shkola-onlajn-krt.ru]лбс это[/url] Не мучайте детей Перешлите другим родителям кто устал от школы

  2159. RockyRoano

    Now leaving a small mental note to recommend this when the topic comes up in conversation, and a look at garnetharbormerchantgallery extended that recommend ready feeling, content that arms me with shareable references for likely future conversations is content with social value and this site is providing that conversational ammunition consistently for me lately.

  2160. shkola onlain_jamn

    Слушайте кто ищет выход Каждое утро как каторга Только оценки и нервотрёпка Короче, нашли идеальное решение — школа онлайн с индивидуальным расписанием Уроки тогда когда удобно В общем, вся инфа вот здесь — образовательные онлайн школы [url=https://shkola-onlajn-lzn.ru]https://shkola-onlajn-lzn.ru[/url] Хватит мучить себя и ребёнка Перешлите другим родителям

  2161. DustinSKymn

    Picked up on several small touches that suggest a careful editor, and a look at wheatcovemerchantgallery suggested the same hand at work across the broader site, editorial consistency at a granular level is one of the strongest signs that an operation is serious rather than just hobbyist and this site reads as serious throughout.

  2163. Vaughnjah

    Now understanding why someone recommended this site to me a while back, and a stop at singersorbet explained the recommendation, sometimes recommendations make sense only after experience and this site has finally clicked into place as the kind of resource I now understand was being recommended for sound editorial reasons by my friend.

  2164. Tyronefen

    Thank you for being clear and direct, that simple approach saves so much frustration on the reader’s end, and a stop at heliofine only made me more sure of it, the rest of the content seems to follow the same pattern which is a great sign of consistent editorial care behind the scenes.

  2165. MalcolmSax

    Will be passing this along to a few people who would benefit from the perspective shared here, and a stop at nyxsip only added to what I will be sharing, this kind of generous content deserves to circulate widely rather than getting buried in some search engine algorithm tweak that pushes it down the rankings.

  2166. Tylerraile

    Coming back tomorrow when I can give this a proper read, the post deserves better attention than I can give right now, and a look at sodasherpa suggests there is plenty more here that deserves the same treatment, definitely a site I will be exploring properly over the next few days when I can.

  2168. BertramNot

    Worth marking this site as one to come back to deliberately rather than by accident, and a stop at sheentiny reinforced that intention, the difference between sites I find again by chance and sites I return to on purpose is meaningful and this one has clearly moved into the deliberate return category for me.

  2169. XavierKeymn

    Thank you for being clear and direct, that simple approach saves so much frustration on the reader’s end, and a stop at hugbox only made me more sure of it, the rest of the content seems to follow the same pattern which is a great sign of consistent editorial care behind the scenes.

  2170. PierreSof

    Approaching this site through a casual link click and being surprised by what I found, and a look at tornadovapor extended the surprise, the rare experience of stumbling into excellent independent content rather than predictable mediocrity is one of the actual remaining pleasures of casual web browsing and this site provided it cleanly.

  2171. EdwardFax

    Vague feelings of recognition kept surfacing as I read because the writing names things I have been thinking, and a look at hiltkindle produced more of those recognition moments, content that gives shape to private intuitions is content that makes me feel less alone in my own thinking and this site has that effect.

  2173. NicholasAlulk

    Now noticing that the post avoided the temptation to be funny in places where humour would have undermined the substance, and a stop at goldenharborcommercegallery maintained the same restraint, knowing when to be serious is a rare editorial virtue and this site has clearly developed it through what I assume is careful editorial practice over years.

  2174. LinwoodHat

    Started smiling at one paragraph because the writing was just nice, and a look at walnutharborcommercegallery produced a couple more such moments, prose that produces small spontaneous reactions in the reader is doing more than just transferring information and the writers here are clearly hitting that level fairly consistently throughout pieces.

  2175. Jaxonjed

    Most of my reading time goes to a small number of trusted sources and this one is now joining that group, and a stop at acornharbortradegallery reinforced the group membership, the few sites that earn a place in my regular rotation are sites I expect ongoing returns from and this one has earned that elevated position consistently.

  2176. DerrickCip

    Now recognising that this site has earned a place in the small group of resources I treat as authoritative, and a stop at thatchteapot confirmed that placement, the difference between resources I trust and resources I just consume is real and this site has clearly moved into the trusted category through consistent quality over time.

  2177. Tannerweite

    Appreciate the work that went into laying this out so clearly, every section earns its place without filler, and a look at gribump confirmed the same care, definitely the kind of place that deserves a return visit when the topic comes up again later in the future or for any related question.

  2178. JuddWex

    Generally my comment to other readers about new sites is to wait and see but for this one I would jump to recommend now, and a look at crearena reinforced that early recommendation, the speed at which a site earns my recommendation is itself a quality signal and this one has earned mine quickly clearly.

  2179. DariusCAK

    Liked the way the post got out of its own way, and a stop at hewzap extended that invisible craft, the best writing you barely notice while reading because it is doing its work without drawing attention to itself and this site has clearly mastered that disappearing act across the pieces I have read.

  2180. Daxfut

    Thanks for putting this online without locking it behind email signups or paywalls, and a quick visit to gildedcovemerchantgallery kept that open feel going, content that trusts the reader to come back rather than gating access is the kind of approach I will reward with regular return visits over time happily.

  2181. Terrellcig

    Appreciated that the writer trusted the reader to follow along without constant restating of earlier points, and a look at kraftkilt continued that respect for the reader, treating an audience as capable adults rather than as people to be hand held through every paragraph is something I notice and value highly across the open internet today.

  2182. Paxtonrup

    Grateful for posts like this one, they remind me there are still places online run by people who care about quality, and a look at wildorchardmerchantgallery reflected the same standards, you can tell the difference between content made for readers and content made just for search engines today and this is the former.

  2183. TravisOmict

    Solid quality, the kind of work that holds up to a careful read rather than a quick skim, and a quick look at pearlharborcommercegallery kept that standard going strong, content that rewards attention rather than punishing it is something I appreciate more and more these days online across nearly every topic I follow.

  2184. Bernardfew

    A piece that earned its conclusions through the body rather than asserting them at the end, and a look at swansignal maintained the same earned quality, conclusions that follow from what came before are more persuasive than declarations and this site has clearly internalised that principle in how it constructs arguments throughout pieces.

  2185. Hoseatoils

    Decided to set a calendar reminder to revisit, and a stop at galekraft extended that revisit list, calendar entries for content are a level of commitment I rarely make but when I do they signal a higher regard than a simple bookmark and this site has earned that calendar tier of relationship from me today.

  2186. Glenaudix

    Now sitting back and recognising that this was a small but real win in my reading day, and a stop at tasseltrace extended that quiet win, the cumulative effect of small reading wins versus the cumulative effect of small reading losses is real over time and this site is contributing to the wins side of that ledger.

  2188. RodneyOxync

    Probably the kind of site that should be more widely read than it appears to be, and a look at tundratoken reinforced that quiet wish, the gap between a sites quality and its apparent reach is sometimes large and that gap exists for this site in a way that makes me want to mention it more.

  2189. Ledgertrump

    Liked the post enough to read it twice and the second read found new things, and a stop at scenictrader similarly rewarded the second look, content with hidden depths that only reveal themselves on careful rereading is the rare kind that earns lasting respect rather than fleeting first impressions only briefly held.

  2190. Logantycle

    A piece that brought a sense of order to a topic I had been finding chaotic, and a look at sonarsandal continued that organising effect, content that imposes useful structure on messy subjects is doing genuine intellectual work and this site is providing that organisational function across multiple posts I have read recently here.

  2192. CarterCob

    Thanks again for the post, I learned a couple of things I can actually use later this week, and after I went over holmglobe the rest of the site looked equally promising, definitely going to spend more time here when I get a free moment over the weekend to read more carefully.

  2193. Burtonnor

    Now adjusting my expectations upward for the topic based on this post, and a stop at irotix continued that bar raising effect, content that resets what I think is possible on a subject is doing real work in shaping my standards and this site is providing those bar raising experiences at a notable rate during sessions.

  2194. JabariMeawl

    A piece that did exactly what it promised in the headline without overshooting or underdelivering, and a look at iciclebrookcommercegallery continued that calibration, alignment between promise and delivery is a basic editorial virtue that many sites fail at and this site has clearly mastered the matching of expectation and substance throughout pieces.

  2195. Vincentwes

    Reading this prompted me to clean up some old notes related to the topic, and a stop at windharborcommercegallery extended that organising urge, content that triggers personal organisation rather than just consuming attention is content with motivating energy and this site has the kind of clarity that prompts active follow up rather than passive consumption.

  2196. Eganfat

    Stands apart from similar pages by actually being useful, that is high praise these days, and a look at auroracovegoodsgallery kept that standard going, you can tell when a site is built around the reader versus around metrics and this one clearly belongs to the first category for sure based on what I read.

  2197. Lloydclory

    Honestly impressed, did not expect to find this level of care on the topic, and a stop at heliogust cemented the impression, you can tell within the first few paragraphs whether a site is going to be worth the time and this one delivered on that early promise nicely throughout the rest of what I read.

  2198. Grahamdof

    A piece that took its time without dragging, and a look at gildedgrovecommercegallery kept the same patient pace, the difference between unhurried and slow is a fine editorial distinction and this site has clearly found the unhurried side without slipping into the slow side which would have lost me as a reader quickly otherwise.

  2199. HarrisonRax

    Bookmark folder reorganised slightly to make this site easier to find, and a look at grohax earned the same accessibility upgrade, the small organisational moves I make for sites I expect to return to often are themselves a signal of how much I trust them and this site triggered those moves naturally.

  2200. Kentonmar

    The examples really helped me grasp the points faster than abstract descriptions would have, and a stop at oxaboon added a few more practical illustrations that drove the message home, the kind of writing that knows its readers learn better through concrete situations rather than vague generalities is rare and worth recognising clearly.

  2202. shkola onlain_uvki

    Всем привет родители Учителя которые только оценками меряют Никакой мотивации учиться Короче, нашли отличный вариант — школа онлайн с государственным аттестатом Аттестат настоящий как в обычной школе В общем, там программа и условия — среднее образование онлайн [url=https://shkola-onlajn-bxf.ru]https://shkola-onlajn-bxf.ru[/url] Не мучайте себя и детей Перешлите другим родителям

  2203. shkola onlain_syOn

    Народ у кого дети Дневники эти вечные Одни оценки и бесконечные поборы Короче, реально крутая система — школы дистанционного обучения с индивидуальным подходом Аттестат государственный В общем, сохраняйте себе — онлайн школы егэ [url=https://shkola-onlajn-vem.ru]https://shkola-onlajn-vem.ru[/url] Переходите на нормальное обучение Перешлите другим родителям

  2204. IsaiahImmor

    Thanks for not padding this with the usual filler intros and outros that every other blog seems to require, and a quick visit to zencovemerchantgallery continued that lean approach across more posts, content stripped of waste is content that respects you and I will always come back to that kind of approach.

  2205. KrisCrort

    A nicely understated post that does not shout for attention, and a look at vortextrance maintained the same quiet quality, understatement is a stylistic choice that distinguishes serious writing from attention seeking writing and this site has clearly committed to the understated approach as a core editorial value rather than just a phase.

  2206. Griffinapary

    Worth your time, that is the simplest endorsement I can give, and a stop at galloheron extends that endorsement across the rest of the site, this is one of those increasingly rare places that delivers on what it promises rather than over selling the content and under delivering on substance every time which I find frustrating elsewhere.

  2207. DevinMossy

    Considered against the flood of similar content this one stands apart in important ways, and a stop at buycoreshop extended that distinctive feel, sites that find their own corner of a crowded topic and stay there are sites worth following and this one has clearly carved out its own space and committed to defending it carefully.

  2208. Buddyalazy

    Speaking from the perspective of a fairly demanding reader the writing here clears the bar consistently, and a look at waferturtle continued clearing that bar, the calibration of demanding reader is something I apply to all sources and this site has been one of the few that handles the demanding reading well across pieces sampled.

  2209. JacobRum

    Once I trust a site this much I tend to read everything they publish and that is the trajectory I am on with this one, and a stop at idebrim confirmed the trajectory, the rare progression from interested reader to comprehensive reader is something only certain sites earn and this one is earning that progression rapidly.

  2210. NikoGal

    Generally my comment to other readers about new sites is to wait and see but for this one I would jump to recommend now, and a look at hugtix reinforced that early recommendation, the speed at which a site earns my recommendation is itself a quality signal and this one has earned mine quickly clearly.

  2211. Quinnfum

    During my morning reading slot this fit perfectly into the routine, and a look at valuecartshop extended that perfect fit into the rest of the routine, content that matches the rhythm of how I actually read rather than demanding accommodation from my schedule is content well calibrated to its likely audience and this site has it.

  2212. Herbertjoupt

    Closed the tab with a small sense of finality rather than the usual rushed exit, and a stop at cricap produced the same considered closing, when reading ends with deliberate satisfaction rather than impatient skip you know the time was well spent and this site is producing those satisfying endings consistently across what I read.

  2215. zabori pod kluch v Moskve_jmOr

    Слушайте кто забор ставил Объездил кучу контор — везде одно и то же То вообще приезжают и говорят что замер не тот Короче, мужики с руками из правильного места — установка заборов в Московской области недорого Гарантия на все работы В общем, вся инфа вот здесь — установка заборов в Московской области [url=https://zagorodnii-dom.ru]установка заборов в Московской области[/url] Не ведитесь на дешёвые предложения Перешлите тому у кого участок

  2216. EnriqueFEW

    Quiet confidence runs through the whole post, no need to shout to make the points stick, and a stop at thriftsundae carried that same restrained voice forward, content that respects the reader by trusting its own substance rather than dressing it up in theatrical language is what I look for online and rarely actually find these days.

  2217. Willisbioky

    Took the time to read every paragraph rather than skimming for the punchline, and a quick visit to turbinevault earned the same careful attention from me, that is the highest signal I can give about content quality because my default mode is rapid scanning rather than deliberate reading on most pages.

  2218. shkola onlain_bxmn

    Мамы и папы всем привет Двойки и замечания в дневнике Ребёнок раздражённый Короче, школа без стресса и скандалов — онлайн обучение для детей в удобном темпе Уроки тогда когда удобно В общем, вся инфа вот здесь — московская онлайн школа [url=https://shkola-onlajn-lzn.ru]https://shkola-onlajn-lzn.ru[/url] Хватит мучить себя и ребёнка Перешлите другим родителям

  2219. TrentNeeme

    Bookmark folder created specifically for this site, and a look at sageharborcraftcollective confirmed the dedicated folder was the right call, dedicated folders for individual sites are a level of organisation I rarely deploy and this site has earned that level of dedicated tracking based on the consistency I have seen so far across sessions.

  2220. Kilepab

    Easily one of the better explanations I have read on the topic, and a stop at pineharbortradegallery pushed it even higher in my mental ranking of useful resources, the kind of site that beats the average not by trying harder but by simply caring more about what it puts out daily which always shows.

  2221. Roderickfrify

    Looking forward to seeing what gets published next month, and a look at solostarlit extended that anticipation across the broader site, finding myself looking forward to a sites future content rather than just consuming its existing content is a stronger commitment level than I usually reach with new finds and this site triggered that.

  2222. NoelVes

    Such writing is increasingly rare and worth supporting through attention, and a stop at hopiron extended that supportive attention across more pages, the conscious choice to spend time on sites that produce careful work rather than convenient consumption is itself a small form of patronage and this site is receiving that conscious patronage from me.

  2223. Fabianaspen

    Top notch writing, every paragraph carries weight and nothing feels like filler, and a stop at sambavarsity reflected that same care, a rare thing on the open web these days where most pages exist for clicks rather than actual reader value or anything close to that which is honestly a real shame.

  2224. Percywit

    Beats most of the alternatives on the topic by a noticeable margin, and a look at gingerwoodcommercegallery did not change that at all, this is one of the better corners of the open internet for this kind of content and I am glad I clicked through rather than skipping past quickly like I usually do.

  2226. Jimjap

    Nice to see a post that does not try to overcomplicate the basics for the sake of looking smart, and once I looked at irubelt the same direct tone was there too, which honestly makes a difference when you are short on time and want answers without long pointless intros.

  2227. Franklinfub

    Just enjoyed the experience without needing to think about why, and a look at juniperharborcommercegallery kept that effortless feeling going, sometimes the best content is invisible in the sense that you forget you are reading until you reach the end and realise time has passed without you noticing it pass naturally.

  2228. KerryDix

    Worth flagging that the post handled an angle of the topic I had not seen elsewhere, and a look at windharbormerchantgallery extended that fresh treatment, content that finds underexplored corners of well covered subjects is genuinely valuable and this site has demonstrated that exploratory editorial approach across multiple pieces in my reading sessions today.

  2229. alkoholizem_vipn

    Zdravo, ljudje. Dolgo časa nisem vedel, kam naprej. Ko gre za odvajanje od alkohola — to je res težka zadeva. Prijatelj mi je svetoval en center, kjer ne obetajo nemogočega. Govorim o Dr Vorobjev centru. Več informacij je na voljo tu: zdravljenje alkoholizma [url=https://www.alkoholizem-zdravljenje.com]zdravljenje alkoholizma[/url] Najboljša odločitev, kar sem jih kdaj sprejel. Odvisnost od alkohola je bolezen, ne sramota. Ampak ko enkrat najdeš pravo pomoč — življenje dobi nov smisel. Več kot vredno je poskusiti. Srečno na tej poti!

  2230. alkoholizem_gwSn

    Že dolgo nisem vedel, kako naprej. Potem pa sem naletel na eno mesto in vse se je spremenilo. Govorim o odvajanju od alkohola pri Dr Vorobjevu. Veste, odvisnost od alkohola ni sramota. In kar je najpomembneje – lahko ostanete doma. Več o tem in o izkušnjah pacientov si lahko preberete neposredno na uradnem viru: zdravljenje alkoholizma [url=www.zdravljenjealkoholizma.com]zdravljenje alkoholizma[/url]. Meni so resnično pomagali.

    Če vi ali kdo od vaših bližnjih se sooča s to težavo – najboljša odločitev je poklicati. Srečno!

  2231. RenebeN

    My professional context would benefit from having this kind of resource available, and a look at gildedcovegoodsroom extended the professional applicability, the rare site that contributes meaningfully to professional work rather than just personal interest is content with multiplied value and this one is providing that professional utility consistently across multiple pieces.

  2232. Alansaf

    Glad to have another reliable bookmark for this topic, and a look at skeinsequoia suggested several more pages I will be marking too, building a personal library of trustworthy resources is one of the actual rewards of careful browsing and this site is earning a place on my permanent shortlist for the topic.

  2233. Jimrem

    Came away with a small but real shift in perspective on the topic, and a stop at gunbolt pushed that shift a bit further, the kind of subtle reframing that good writing does to a reader without making a big deal of it is something I always appreciate when it happens which is sadly not that often.

  2234. ArnoldHes

    Skipped lunch to finish reading, which says something, and a stop at gallohex kept me at my desk longer than planned, when content beats the lunch impulse the writer has done something genuinely impressive in an attention environment full of immediately satisfying alternatives competing for the same finite block of reader time.

  2235. alkoholizem_rmpa

    Veliko sem prebral in slišal o tem. Ko sem prvič slišal za ambulantno zdravljenje alkoholizma po metodi Dr Vorobjeva, sem bil neveren. Ampak ko sem prebral izkušnje anderen — ugotovil sem, da to res deluje. Odvisnost od alkohola je strašna bolezen. In najhuje je, da ne poznajo dobrih možnosti zdravljenja. Zato svetujem, da si vzamete čas in preberete posodobljene podatke, ki so na voljo na tej povezavi: Dr Vorobjev [url=www.alkoholizma-zdravljenje-si.com]www.alkoholizma-zdravljenje-si.com[/url]. Več o tem si preberite na spodnji povezavi.

    Meni je ta pristop pomagal. Če vas to zanima — vzemite si čas in preberite. Upam, da vam bo koristilo!

  2236. Bertunoni

    Felt the post had been written without looking over its shoulder, and a look at zenharborcommercegallery continued that confident posture, content written for its own sake rather than against imagined critics has a different quality and this site reads as written from a place of confidence rather than defensive justification of every claim.

  2239. Harleybug

    Just want to acknowledge that the writing here is doing something right, and a quick visit to starlitvixen confirmed the same standards run across the broader site, recognising good work is something I try to do when I find it because the alternative is silence and silence rewards mediocrity.

  2244. Jabarimup

    Quietly impressive in a way that does not announce itself, and a stop at buyersmarket extended that quiet impressiveness, the kind of quality that emerges through sustained attention rather than first impressions is the kind I trust more deeply and this site has been earning that deeper trust across multiple sessions over time consistently.

  2245. Lucasdedly

    Took something from this I did not expect to find, and a stop at humvat added another unexpected useful piece, content that exceeds expectations rather than just meeting them is the kind that builds enthusiasm and earns repeat visits without any explicit ask from the writer or platform behind the work being read.

  2246. Tatemug

    Bookmark earned and the bookmark feels like a permanent addition rather than a maybe, and a look at valecovegoodsgallery confirmed that permanent status, the difference between durable bookmarks and ephemeral ones is something I have learned to feel quickly and this site triggered the durable feeling almost immediately during my first read here.

  2247. SamuelKic

    Excellent execution from start to finish, the post never loses its rhythm and the points stay sharp, and a quick stop at crystalbuyhub kept the same level going, consistency like this across a site is the marker of a serious operation rather than a casual side project running on autopilot somewhere else.

  2248. KobeOxync

    Thanks for the honest framing without exaggerated claims that the topic will change my life, and a stop at uptonstarlit kept the same modest tone, restraint in marketing language signals trustworthiness and the writers here are clearly playing the long game by building credibility rather than chasing immediate clicks through hyperbole.

  2249. Eliascup

    My professional context would benefit from having this kind of resource available, and a look at valueshoppinghub extended the professional applicability, the rare site that contributes meaningfully to professional work rather than just personal interest is content with multiplied value and this one is providing that professional utility consistently across multiple pieces.

  2250. Garrettvok

    Useful information presented in a way that does not feel like a sales pitch, that is what I appreciated most, and a stop at vocabtoffee was the same, no upsell and no fake urgency just steady content laid out properly for someone trying to actually learn from it rather than just be sold to.

  2251. OtisGow

    Worth recognising that the post did not pretend to be the final word on the topic, and a stop at heliohex continued that humility, content that admits its own scope and limits is more trustworthy than content that overreaches and this site has clearly developed the editorial maturity to know what it can and cannot claim well.

  2252. Normansoigo

    Solid little post, the kind that does not need to be flashy because the substance is doing the work, and a look at cyljax kept that quiet confidence going across the site, this is what writing looks like when the writer trusts the content to land on its own without theatrics or unnecessary attention seeking behaviour.

  2253. Daltonjew

    Thanks for the honest framing without exaggerated claims that the topic will change my life, and a stop at hueheron kept the same modest tone, restraint in marketing language signals trustworthiness and the writers here are clearly playing the long game by building credibility rather than chasing immediate clicks through hyperbole.

  2254. Wallacecen

    Took longer than expected to finish because I kept stopping to think, and a stop at gladeharborcommercegallery did the same to me, content that provokes thought rather than just delivering information is in a different category and the team here is clearly working at that higher level rather than just cranking out posts.

  2255. AbelSmult

    Probably this is one of the better quiet successes on the open web at the moment, and a look at krillflume reinforced that quiet success quality, sites that are doing well without making a noise about doing well are the sites I most respect and this one has clearly chosen the quiet success path consistently throughout.

  2256. alkoholizem_xvSn

    Res je težko priznati si, da rabiš pomoč. Potem pa sem naletel na eno mesto in vse se je postavilo na svoje mesto. Govorim o zdravljenju alkoholizma pri Dr Vorobjevu. Veste, alkoholizem je bolezen, ne slabost. In kar je najpomembneje – lahko ostanete doma. Vse informacije in izkušnje drugih sem podrobno pregledal na spletni strani, posodobljene podatke pa si lahko ogledate tukaj: zdravljenje alkoholizma [url=https://zdravljenjealkoholizma.com]zdravljenje alkoholizma[/url]. Meni so resnično pomagali.

    Če vi ali kdo od vaših bližnjih se sooča s to težavo – ne odlašajte. Srečno!

  2258. JamarcusGeade

    A piece that left me thinking I had been undercaring about the topic, and a look at jekcar reinforced that mild concern, content that raises the appropriate weight of a subject without being preachy about it is doing important work and this site is providing that gentle elevation of attention for me consistently.

  2259. alkoholizem_oepn

    Zdravo, ljudje. Preizkusil sem že vse mogoče. Ko gre za odvajanje od alkohola — ni šala. Prijatelj mi je svetoval en center, kjer res vedo, kaj delajo. Govorim o Dr Vorobjev. Vse podrobnosti in izkušnje drugih ljudi najdete tukaj: ambulantno zdravljenje alkoholizma [url=https://www.alkoholizem-zdravljenje.com]https://www.alkoholizem-zdravljenje.com[/url] Meni so res pomagali. Ni lahko priznati si, da imaš težavo. Ampak ko enkrat najdeš pravo pomoč — upanje se vrne. Vsekakor priporočam vsem, ki se spopadajo s to težavo. Srečno na tej poti!

  2260. KobeFup

    Most of my reading time goes to a small number of trusted sources and this one is now joining that group, and a stop at temposofa reinforced the group membership, the few sites that earn a place in my regular rotation are sites I expect ongoing returns from and this one has earned that elevated position consistently.

  2261. AlvinGop

    Speaking as someone who used to recommend blogs frequently and got out of the habit this site is rekindling that impulse, and a look at pyxedge extended the rekindling, the recovery of an old habit triggered by encountering work that justifies it is itself a small kind of pleasure and this site is providing that recovery experience.

  2262. ErikJoirm

    Now feeling the rare pleasure of trusting a source completely on first encounter, and a look at caramelcovemarketgallery extended that initial trust into something more durable, the calibration of trust to evidence is something I do informally and this site has earned high trust through the cumulative weight of multiple consistently good posts already.

  2263. DavidMow

    Worth flagging this site to a few specific friends who would appreciate the editorial sensibility, and a look at kettlecrestmerchantgallery added more pages I will mention to them, recommending sites to specific people requires understanding both the site and the person and this site is making those personalised recommendations easy and natural for me.

  2264. BjornLooky

    This actually answered the question I had been searching for, and after I checked lanternorchardvendorparlor I had a few more pieces I had not realised I needed, that is the sign of a site that knows what its readers want before they even know how to ask it which is impressive.

  2265. Oscarstido

    Came across this and immediately thought of a friend who would enjoy it, and a stop at irubrisk also reminded me of someone, content that triggers the urge to share is content that has earned my recommendation and this site has earned multiple from me already across different conversations during the week.

  2266. KyrieJocky

    A piece that exhibited the kind of patience that good writing requires, and a look at woodcovevendorparlor continued that patient quality, hurried writing is easy to spot and this site reads as having been written without time pressure which produces a different feel than the rushed content that dominates much of the modern blog space.

  2267. GichardDuago

    You have managed to summarize a rather extensive amount of information into a highly easy-to-follow format that keeps the reader engaged from the very first paragraph all the way down to your concluding thoughts today.

    FEZbet

  2268. DeonDak

    Worth marking this site as one to come back to deliberately rather than by accident, and a stop at swapvenom reinforced that intention, the difference between sites I find again by chance and sites I return to on purpose is meaningful and this one has clearly moved into the deliberate return category for me.

  2269. WestonEdgem

    Saving the link for sure, this one is a keeper, and a look at gyrarena confirmed I should bookmark the entire site rather than just this page, the consistency across what I have seen so far suggests there is a lot more here worth coming back for soon when I have more time.

  2270. Marvintug

    Glad to have another data point on a question I am still thinking through, and a look at trenchtwist added two more, content that acknowledges its place in a wider conversation rather than pretending to settle the question alone is intellectually honest in a way that I wish was more common across the open web.

  2275. alkoholizem_ntpa

    Veliko sem prebral in slišal o tem. Ko sem prvič slišal za zdravljenje alkoholizma po metodi Dr Vorobjeva, sem bil skeptičen. Ampak ko sem spoznal ljudi, ki jim je uspelo — vse se je spremenilo. Odvisnost od alkohola je strašna bolezen. In najhuje je, da mnogi ne vedo, kam se obrniti. Zato vam želim pokazati vse tehnične podrobnosti in uradne informacije, ki so na voljo na tej povezavi: Dr Vorobjev [url=http://www.alkoholizma-zdravljenje-si.com]http://www.alkoholizma-zdravljenje-si.com[/url]. Na tej povezavi so odgovori na vsa vprašanja.

    Po dolgih letih sem končno našel rešitev. Če se soočate s podobno težavo — ne odlašajte. Srečno vsem na tej poti!

  2276. Tatemug

    Looking through the archives suggests this site has been doing this for a while at this level, and a look at valecovegoodsgallery confirmed the long term consistency, sites that have maintained quality across years rather than just a recent stretch are sites with serious editorial discipline and this one has clearly been at it for a while.

  2277. Chancehex

    Liked how the writer used real examples instead of theoretical ones to make the points stick, and a stop at buyspotstore added even more concrete examples, this is the kind of practical approach that respects readers who actually want to apply what they learn rather than just nodding along passively without doing anything useful.

  2278. Austinbuh

    Now feeling something close to gratitude for the fact this site exists, and a look at stashsuperb extended that gratitude, the rare site that produces this kind of response is the rare site worth defending in conversations about whether the modern internet is still capable of producing genuinely valuable independent content for serious adults.

  2279. alkoholizem_cuSn

    Dolga leta sem se boril sam. Potem pa sem izvedel za center in vse se je začelo obračati na bolje. Govorim o zdravljenju alkoholizma pri Dr Vorobjev centru. Veste, odvisnost od alkohola ni sramota. In kar je najpomembneje – ni treba v bolnišnico. Vse informacije in izkušnje drugih sem podrobno pregledal na spletni strani, posodobljene podatke pa si lahko ogledate tukaj: Dr Vorobjev [url=https://zdravljenjealkoholizma.com]https://zdravljenjealkoholizma.com[/url]. Meni so resnično pomagali.

    Če vi ali kdo od vaših bližnjih se sooča s to težavo – najboljša odločitev je poklicati. Držim pesti!

  2280. shkola onlain_daki

    Всем привет родители Замучились мы с этой школой А эти бесконечные ремонты в классе Короче, реально удобный и простой — онлайн обучение для детей в любое время Аттестат настоящий как в обычной школе В общем, смотрите сами по ссылке — онлайн средняя школа [url=https://shkola-onlajn-bxf.ru]https://shkola-onlajn-bxf.ru[/url] Не мучайте себя и детей Перешлите другим родителям

  2281. Cainrhymn

    The post made the topic feel approachable without making it feel trivial, that is a fine balance, and a stop at sharesignal maintained the same balance, finding the middle ground between welcoming and serious is genuinely difficult and the writers here have clearly figured out how to consistently hit it well across many different posts.

  2282. Bertwheed

    A memorable post for me on a topic I had thought I was tired of, and a look at glassmeadowcommercegallery suggested the same site can refresh other tired topics, sites that can revive my interest in subjects I had written off as exhausted are doing rare work and this one is clearly doing that for me today.

  2283. Shanehycle

    Honestly informative, the writer covers the ground without showing off, and a look at digitaltrendstation reflected the same humility, content that respects the reader rather than trying to dazzle them is something I always appreciate and rarely come across in this corner of the internet today across the topics I usually read.

  2284. zabori pod kluch v Moskve_jrOr

    Владельцы участков отзовитесь Сроки срывают постоянно То вообще приезжают и говорят что замер не тот Короче, мужики с руками из правильного места — монтаж заборов под ключ с материалами Цены ниже чем у других на 30% В общем, там каталог и цены — изготовление заборов на заказ [url=https://zagorodnii-dom.ru]изготовление заборов на заказ[/url] Не ведитесь на дешёвые предложения Перешлите тому у кого участок

  2285. GriffinRek

    Honest take is that I will probably forget most of what I read online today but this post is one I will remember, and a stop at huejuly kept that same memorable quality going, certain writing leaves a residue in the mind in a way most content simply does not manage.

  2286. alkoholizem_dzpn

    Pozdravljeni. Preizkusil sem že vse mogoče. Ko gre za odvajanje od alkohola — veliko ljudi se muči v tišini. Prijatelj mi je pokazal en center, kjer res vedo, kaj delajo. Govorim o Dr Vorobjev centru. Vse podrobnosti in izkušnje drugih ljudi najdete tukaj: Dr Vorobjev [url=alkoholizem-zdravljenje.com]alkoholizem-zdravljenje.com[/url] Po nekaj tednih sem začutil razliko. Prvi korak je vedno najtežji. Ampak ko vidiš, da nisi sam — vse postane lažje. Več kot vredno je poskusiti. Vsak nov dan je priložnost.

  2287. CedricCok

    Worth pointing out the careful word choice in this post, no buzzwords and no jargon, and a look at lanternmeadowcommercegallery continued that disciplined vocabulary, sites that resist the pull of trendy language are sites that will read well in five years and this one is clearly built for that kind of long durability.

  2288. GriffinNiz

    Useful enough to recommend to several people I know who would appreciate it, and a stop at cloverharborcommercegallery added more material I will pass along too, the kind of writing that earns word of mouth is the kind that actually delivers on its promises which is what this site does without any drama or fanfare attached.

  2289. KeaganMaf

    Liked that the post landed without needing to manufacture controversy or take a contrarian stance for attention, and a stop at opalrivergoodsgallery continued that grounded approach, content that earns attention through quality rather than provocation is the kind that builds long term trust rather than burning it on quick wins.

  2290. SeanPaype

    Compared to the usual results for this kind of search this site stands well above the average, and a quick visit to dahbrood kept the standard high, you can tell within seconds whether a site is going to waste your time or actually deliver and this one clearly delivers without any false starts.

  2291. Jacksonpsymn

    Picked up several practical tips that I plan to try out this week, and a look at trophysofa added a few more I will be testing alongside, content with practical hooks that connect to my actual life is the kind that earns my repeat attention rather than the merely interesting that I forget within a day.

  2292. Darnellimibe

    Comfortable read, finished it without realising how much time had passed, and a look at kudosember pulled me into more pages the same way, the absence of friction in good content lets time disappear and that is one of the highest compliments I can pay any piece of writing I find online during a regular search session.

  2293. Kobelit

    Reading carefully here has reminded me what reading carefully feels like, and a look at uppersharp extended that reminder, the experience of careful reading versus skimming is different in ways I had partially forgotten and this site has clearly refreshed my memory of what attention feels like when content rewards it consistently.

  2294. LonnieLib

    A welcome reminder that thoughtful writing still happens online, and a look at opalrivercraftcollective extended that reassurance, the modern web makes it easy to forget that careful writing exists and finding sites that practice it is a small antidote to the cynicism that builds up from too much exposure to algorithmic content.

  2295. Lewisfoush

    I was genuinely pleased to discover this article today because it manages to deliver a very easy-to-follow and neutral overview of the subject without getting bogged down in unnecessary details or overly complex jargon that confuses readers.

    viagra pills sexual xxx porn pills

  2296. Franciscocop

    A piece that prompted a small mental rearrangement of how I order related ideas, and a look at sorreltavern extended that rearranging effect, content that affects the structure of my thinking rather than just adding to it is content with the deepest kind of impact and this site is reaching that depth for me today.

  2297. BernardNuh

    Different feel from the algorithmically optimised posts that dominate the topic, and a stop at silvercovecraftcollective reinforced that human touch, you can tell when a site is being run by someone who reads what they publish versus someone just hitting submit and moving on quickly to the next assignment without checking the result.

  2298. Liammaive

    Most posts I read end up forgotten within a day but this one is sticking, and a look at heliojuly extended that lingering effect, content that survives the immediate moment of reading rather than evaporating is content with genuine retention quality and this site has been producing memorable pieces at a rate notable across my reading.

  2299. Mylesboync

    Came away with a small but real shift in perspective on the topic, and a stop at kettleharborcommercegallery pushed that shift a bit further, the kind of subtle reframing that good writing does to a reader without making a big deal of it is something I always appreciate when it happens which is sadly not that often.

  2300. LesterEract

    Picked up something useful for a side project, and a look at pearlharborvendorparlor added another piece I will incorporate, content that connects to specific projects I am working on is content with practical utility and the practical utility of this site is showing up across multiple posts I have read in the last hour or so.

  2301. Devinnub

    Felt like the writer was speaking directly to someone with my level of curiosity, neither talking down nor showing off, and a stop at slackvista kept that comfortable matching going, finding writing that meets you where you are rather than asking you to climb up or stoop down feels great every time it happens.

  2302. alkoholizem_kuSn

    Že dolgo nisem vedel, kako naprej. Potem pa sem dobil pravi nasvet in vse se je spremenilo. Govorim o zdravljenju alkoholizma pri Dr Vorobjevu. Veste, ni lahko, ampak se da premagati. In kar je najpomembneje – ni treba v bolnišnico. Več o tem in o izkušnjah pacientov si lahko preberete neposredno na uradnem viru: Dr Vorobjev [url=www.zdravljenjealkoholizma.com]www.zdravljenjealkoholizma.com[/url]. Zdaj sem že pol leta trezen in ponosen nase.

    Če nekdo v vaši okolici ne ve, kam se obrniti – najboljša odločitev je poklicati. Držim pesti!

  2303. Georgeedgep

    Came back to this an hour later to reread a specific section, and a quick visit to isebrook also drew a second look, content that pulls you back rather than letting you move on permanently is the kind I want to fill my browser bookmarks with in 2026 and beyond as the open internet evolves.

  2305. Dylanhounc

    Solid little post, the kind that does not need to be flashy because the substance is doing the work, and a look at huijax kept that quiet confidence going across the site, this is what writing looks like when the writer trusts the content to land on its own without theatrics or unnecessary attention seeking behaviour.

  2306. ElijahSab

    Started believing the writer knew the topic deeply by about the second paragraph, and a look at jewbush reinforced that confidence, the speed at which a writer establishes credibility through their writing is a useful quality signal and this writer establishes it quickly and quietly without resorting to credential dropping or self promotion.

  2307. Jeffnip

    Worth saying that this is one of the better things I have read on the topic in months, and a stop at hazelharbormerchantgallery reinforced that ranking, the topic is well covered by many sources but few do it with this level of care and the few that do deserve to be flagged so other readers can find them.

  2309. NathanielSal

    Reading this with a fresh mind in the morning brought out details I might have missed in the afternoon, and a stop at velourudon earned the same fresh attention, content that rewards being read at full attention rather than at energy lows is content with real density and this site has that density consistently.

  2310. Alfredrep

    The overall feel of the post was professional without being stuffy, and a look at walnutharborvendorparlor kept that approachable expertise going, finding the right register for technical content is hard but this site has clearly figured out how to sound knowledgeable without slipping into that distant lecturing tone that loses readers in droves every time.

  2311. TodTem

    Generally I find the content on similar topics frustrating in specific ways and this post avoided all of them, and a look at buytrailshop continued that frustration free experience, content that sidesteps the standard failure modes of its genre is content with editorial awareness and this site has clearly studied what fails elsewhere consistently.

  2312. Arnoldcrors

    Reading carefully this time rather than scanning, and the depth shows up in places I missed first time around, and a look at salutesyrup rewarded the same careful approach, content that holds up to multiple reads is content I want more of in my regular rotation rather than disposable scroll fodder daily.

  2313. alkoholizem_ytpn

    Živjo vsem. Dolgo časa nisem vedel, kam naprej. Ko gre za ambulantno zdravljenje alkoholizma — ni šala. Prijatelj mi je pokazal en center, kjer ne obetajo nemogočega. Govorim o Dr Vorobjev. Preverite sami na povezavi: ambulantno zdravljenje alkoholizma [url=http://alkoholizem-zdravljenje.com]http://alkoholizem-zdravljenje.com[/url] Meni so res pomagali. Prvi korak je vedno najtežji. Ampak ko enkrat najdeš pravo pomoč — vse postane lažje. Več kot vredno je poskusiti. Vsak nov dan je priložnost.

  2314. Tonydrani

    Closed the tab feeling I had spent the time well, and a stop at dailyneedsstore extended that feeling across more pages, the test of whether time on a site was well spent is one I apply silently after closing tabs and very few sites pass it but this one passed it cleanly today afternoon clearly.

  2315. shkola onlain_tdmn

    Здорова родители Домашка на весь вечер Никакого интереса к знаниям Короче, реально удобный формат учёбы — школа онлайн с государственной лицензией Аттестат настоящий В общем, сохраняйте себе — онлайн средняя школа [url=https://shkola-onlajn-lzn.ru]https://shkola-onlajn-lzn.ru[/url] Хватит мучить себя и ребёнка Перешлите другим родителям

  2316. alkoholizem_mipa

    Dolgo sem iskal pravo rešitev. Ko sem prvič slišal za zdravljenje alkoholizma po metodi Dr Vorobjeva, sem bil skeptičen. Ampak ko sem spoznal ljudi, ki jim je uspelo — ugotovil sem, da to res deluje. Odvisnost od alkohola je strašna bolezen. In najhuje je, da ne poznajo dobrih možnosti zdravljenja. Zato vam želim pokazati vse tehnične podrobnosti in uradne informacije, ki so na voljo na tej povezavi: Dr Vorobjev [url=www.alkoholizma-zdravljenje-si.com]www.alkoholizma-zdravljenje-si.com[/url]. Tam boste našli vse potrebne informacije.

    Meni je ta pristop pomagal. Če se soočate s podobno težavo — to je lahko prelomnica v vašem življenju. Srečno vsem na tej poti!

  2317. LukeGed

    Felt energised after reading rather than drained, which is unusual for online content these days, and a look at hullgale continued that good feeling, content that leaves you better than it found you is rare and worth bookmarking when you stumble across it for the first time today or any other day really.

  2318. DamienFride

    Came away with some new perspectives I had not considered before, and after wildharborcommercegallery those ideas felt more complete, the kind of content that stays with you a little while after reading rather than slipping out the moment you switch tabs and move on with your day to whatever comes next.

  2319. RexVek

    A modest masterpiece in its own quiet way, and a look at lavenderharbormerchantgallery confirmed the same quiet quality across the rest of the site, calling something a masterpiece is usually overstating but for content this carefully crafted the word feels appropriate even if the writers themselves would probably resist the label honestly.

  2321. JulianGlits

    Now considering writing a longer note about the post somewhere, and a look at seacovecraftcollective added more material for that note, content that prompts me to write rather than just consume is content with generative energy and this site is producing that generative effect for me at a higher rate than most sources.

  2322. Perrypeach

    Appreciated how the writer anticipated the questions a reader might have along the way, and a stop at spectrasolo continued that thoughtful approach, you can tell when content has been edited with the reader in mind versus just published as a first draft and this is clearly the former approach across what I read.

  2323. Melvinzok

    Most blog writing on this subject reaches for the same handful of arguments and this post avoided them, and a look at cottongrovecommercegallery continued the original treatment, content that finds its own path through territory other writers have flattened is content with real authorial energy and this site has plenty of that distinctive energy.

  2324. ArnoldArice

    Reading this felt productive in a way most internet reading does not, and a look at florabrookvendorfoundry continued that productive feeling, sometimes the open web feels like a waste of time but sites like this remind me why I still bother to look around rather than retreating to old reliable sources for everything I need.

  2325. alkoholizem_ptSn

    Dolga leta sem se boril sam. Potem pa sem naletel na eno mesto in vse se je spremenilo. Govorim o ambulantnem zdravljenju alkoholizma pri Dr Vorobjevu. Veste, ni lahko, ampak se da premagati. In kar je najpomembneje – ni treba v bolnišnico. Več o tem in o izkušnjah pacientov si lahko preberete neposredno na uradnem viru: zdravljenje alkoholizma [url=https://zdravljenjealkoholizma.com]zdravljenje alkoholizma[/url]. Po prvem tednu sem začutil razliko.

    Če vi ali kdo od vaših bližnjih ne ve, kam se obrniti – ne odlašajte. Srečno!

  2326. IvanGog

    Polished and informative without feeling overproduced, that is the sweet spot, and a look at deoblob hit it again, you can tell when a site has been built with care versus thrown together for the sake of having something to put online and this is clearly the former approach taken by the team.

  2327. NevilleAdvag

    Now feeling the rare pleasure of trusting a source completely on first encounter, and a look at rainharbormarketgallery extended that initial trust into something more durable, the calibration of trust to evidence is something I do informally and this site has earned high trust through the cumulative weight of multiple consistently good posts already.

  2329. gryzopodemnoe oborydovanie_kymt

    Слушайте кто подъемники ищет Задолбался я уже оборудование подбирать То вообще отгружают б/у под видом нового Короче, нашел нормальных производителей — производитель грузоподъемного оборудования с гарантией Сертификаты все в наличии В общем, жмите чтобы не потерять — таль электрическая купить [url=https://tal-elektricheskaya.ru]таль электрическая купить[/url] Проверяйте производителя по документам Перешлите тому кто ищет оборудование

  2330. DaquanAnive

    Most of the time I feel the open web is in decline and then I find a site like this, and a stop at coralharborvendorloft reinforced that mood lift, the cumulative effect of finding occasional excellent independent content versus the cumulative effect of finding mostly mediocre content is real for the long term reader maintaining web habits today.

  2331. Dexterswids

    Reading this in pieces during a long afternoon and finding it consistently rewarding, and a stop at futurecartcorner fit naturally into the same fragmented reading pattern, sites whose posts can be read in segments without losing the thread are well suited to how I actually read these days and this one is built well.

  2332. Johanwealf

    Worth saying that the quiet confidence of the writing is what landed first, and a look at tapetoken continued that quiet quality, confident writing without the loud display of confidence is a rare combination and this site has clearly developed both the knowledge and the editorial restraint to land that combination consistently.

  2333. Juliopayog

    A piece that read as if the writer was thinking carefully rather than just typing fluently, and a look at lanternorchardmerchantgallery continued that considered quality, the difference between fluent typing and careful thinking shows up in writing and this site reads as the product of thought rather than just the product of language fluency apparently.

  2334. XavierAneno

    Honestly impressed by the consistency of voice across what I have read so far, and a quick visit to aroarch continued that consistent feel, when a site reads like one careful person rather than a committee the experience is more rewarding for the reader who notices these subtle editorial details over time.

  2335. IsraelSturn

    Thanks for treating the topic with the seriousness it deserves without becoming pompous about it, and a stop at honeycovemerchantgallery continued that balanced treatment, the gap between earnest and self serious is huge and writers who can stay on the right side of it earn my respect when I find them online today.

  2336. Kendrickbip

    Honest reaction is that this is the kind of writing I would defend in a conversation about good blog content, and a look at velvetbrooktradegallery reinforced that, the rare site whose work I would actively recommend rather than just tolerate is the kind I want to support through return visits regularly.

  2337. Blakesmoxy

    Now adding this to a list of sites I want to see flourish, and a stop at ivebump reinforced that wish, the few sites I actively root for are sites that produce the kind of work I want more of in the world and this one has joined that small list based on what I have read so far.

  2338. alkoholizem_ippn

    Zdravo, ljudje. Že dolgo sem iskal resnično rešitev. Ko gre za odvajanje od alkohola — veliko ljudi se muči v tišini. Prijatelj mi je priporočil en center, kjer imajo izkušnje. Govorim o Dr Vorobjev. Več informacij je na voljo tu: ambulantno zdravljenje alkoholizma [url=www.alkoholizem-zdravljenje.com]www.alkoholizem-zdravljenje.com[/url] Najboljša odločitev, kar sem jih kdaj sprejel. Ni lahko priznati si, da imaš težavo. Ampak ko dobiš strokovno podporo — upanje se vrne. Več kot vredno je poskusiti. Srečno na tej poti!

  2340. Skylarcop

    If you asked me to point to a recent positive sign for the open web this site would be near the top, and a stop at huiyam reinforced that designation, the few sites that serve as evidence the web can still produce quality independent content are precious and this one has clearly become one for me.

  2341. Adriansam

    Now sitting back and recognising that this was a small but real win in my reading day, and a stop at tidalurchin extended that quiet win, the cumulative effect of small reading wins versus the cumulative effect of small reading losses is real over time and this site is contributing to the wins side of that ledger.

  2342. VirgilDag

    Worth flagging that the writing rewarded a second read more than I expected, and a look at steamsaunter produced the same second read benefit, content with hidden depths that emerge only on careful rereading is rare in the modern blog space and this site has clearly invested in that level of compositional density throughout.

  2343. MicahAmuct

    Looking back on this reading session it stands as one of the better ones recently, and a look at dailycartdeals extended that ranking, the informal ranking of reading sessions against each other is something I do mentally and this session ranks high largely because of this site and a couple of related pages here.

  2344. Ryannap

    Worth saying that the quiet confidence of the writing is what landed first, and a look at humgrain continued that quiet quality, confident writing without the loud display of confidence is a rare combination and this site has clearly developed both the knowledge and the editorial restraint to land that combination consistently.

  2345. ChaseNed

    Picked this up between two other things I was doing and got drawn in completely, and after helioketo my original tasks were completely forgotten for a while, content that derails a workflow in a positive way by being more interesting than what you were already doing is rare and worth recognising clearly.

  2346. alkoholizem_vuSn

    Dolga leta sem se boril sam. Potem pa sem izvedel za center in vse se je postavilo na svoje mesto. Govorim o zdravljenju alkoholizma pri Dr Vorobjev centru. Veste, alkoholizem je bolezen, ne slabost. In kar je najpomembneje – lahko ostanete doma. Vse informacije in izkušnje drugih sem podrobno pregledal na spletni strani, posodobljene podatke pa si lahko ogledate tukaj: Dr Vorobjev [url=http://www.zdravljenjealkoholizma.com]http://www.zdravljenjealkoholizma.com[/url]. Meni so resnično pomagali.

    Če kogarkoli, ki ga imate radi potrebuje pomoč – ne odlašajte. Srečno!

  2347. Dwayneslipt

    Reading this prompted a small redirection in something I was working on, and a stop at vocabtrifle extended that redirecting influence, content that affects my actual work rather than just my thinking has the highest practical impact and this site is providing that level of influence for me at a sustainable rate apparently.

  2348. StuartTwese

    Took longer than expected to finish because I kept stopping to think, and a stop at silkgroveartisanexchange did the same to me, content that provokes thought rather than just delivering information is in a different category and the team here is clearly working at that higher level rather than just cranking out posts.

  2349. alkoholizem_bzpa

    Že kar nekaj časa spremljam to temo. Ko sem prvič slišal za ambulantno zdravljenje alkoholizma po metodi Dr Vorobjeva, sem bil poln dvomov. Ampak ko sem videl rezultate — ugotovil sem, da to res deluje. Alkoholizem uničuje družine. In najhuje je, da mnogi ne vedo, kam se obrniti. Zato svetujem, da si vzamete čas in preberete posodobljene podatke, ki so na voljo na tej povezavi: Dr Vorobjev [url=https://alkoholizma-zdravljenje-si.com]https://alkoholizma-zdravljenje-si.com[/url]. Tam boste našli vse potrebne informacije.

    Meni je ta pristop pomagal. Če poznate koga, ki potrebuje pomoč — to je lahko prelomnica v vašem življenju. Srečno vsem na tej poti!

  2350. DrewLep

    Honestly impressed by how much useful content sits in such a small post, and a stop at sealtoga confirmed the rest of the site packs a similar punch, density without confusion is a hard balance to strike and this site has clearly cracked the code on it across many different topic areas covered.

  2351. Nealinfes

    Now appreciating that the post did not try to imitate any other style I might recognise, and a stop at elmwoodgoodsroom continued that distinct voice, content with its own register rather than borrowed from elsewhere is content with real authorial presence and this site has clearly developed that presence through what feels like patient editorial work.

  2352. PhilipSar

    A memorable post for me on a topic I had thought I was tired of, and a look at syxbolt suggested the same site can refresh other tired topics, sites that can revive my interest in subjects I had written off as exhausted are doing rare work and this one is clearly doing that for me today.

  2353. Josephfiree

    Genuinely changed how I think about a small piece of the topic, which does not happen often online, and a look at straitsurge added another nudge in the same direction, the kind of writing that earns a small mental shift rather than just confirming what you already thought before reading is a sign of careful thought.

  2354. EduardoJer

    Appreciate the thoughtful approach, the writer clearly took time to make this readable for someone who is not already an expert, and a look at crownharborcommercegallery kept that going nicely, easy on the eyes and easy on the brain which is always a winning combination when reading on a busy day.

  2355. Vincentber

    Reading this in a quiet hour and finding it suited the quiet, and a stop at jasperharbormerchantgallery extended the quiet reading mood, content that matches its own optimal reading conditions rather than fighting them is content that has been thoughtfully calibrated and this site reads as having a particular reading mood in mind throughout.

  2356. MarcusVed

    Looking for similar voices elsewhere has come up empty in my recent searches, and a stop at ixaqua extended the search frustration, the rare site that does what no other does in quite the same way is precious and this one has clearly developed a particular approach that I have not been able to find duplicates of.

  2357. SterlingFer

    Nice to see a post that does not try to overcomplicate the basics for the sake of looking smart, and once I looked at clovercrestmerchantgallery the same direct tone was there too, which honestly makes a difference when you are short on time and want answers without long pointless intros.

  2358. Barrytem

    A piece that suggested careful editing without showing the marks of the editing, and a look at daisycovevendorcorner continued that invisible polish, the best editing disappears into the prose and this site reads as having been edited with skill that does not announce itself which is the highest compliment I can offer any blog content.

  2359. alkoholizem_oxpn

    Pozdravljeni. Preizkusil sem že vse mogoče. Ko gre za odvajanje od alkohola — to je res težka zadeva. Prijatelj mi je svetoval en center, kjer ne obetajo nemogočega. Govorim o Dr Vorobjev. Preverite sami na povezavi: odvisnost od alkohol [url=www.alkoholizem-zdravljenje.com]odvisnost od alkohol[/url] Najboljša odločitev, kar sem jih kdaj sprejel. Odvisnost od alkohola je bolezen, ne sramota. Ampak ko vidiš, da nisi sam — življenje dobi nov smisel. Če kdo dvomi, naj kar pokliče in vpraša. Srečno na tej poti!

  2361. JaimeMoump

    Honestly the simplicity of the explanation made the topic click for me in a way other writeups had not, and a look at quartzorchardartisanexchange continued that clarity into related areas, when a writer gets the level of explanation right the reader does the heavy lifting themselves and the post just enables it.

  2362. RandydrulA

    Held my interest from the opening line through to the closing thought, and a stop at doxfix did the same, content that earns sustained attention in an environment full of distractions is doing something right and this site is clearly doing several things right rather than just one or two which I really appreciate.

  2363. Stuartmox

    Sets a higher bar than most of what shows up in search results for this topic, and a look at directshoppinghub did not lower that bar at all, in fact it confirmed the impression, this is the kind of consistency that earns a place in regular rotation for serious readers instead of casual scrollers passing through.

  2364. CraigBoubs

    Loved the writing voice here, friendly without being fake and confident without being arrogant, and a stop at linencovemerchantgallery carried the same tone forward, the kind of personality that makes a reader feel welcome rather than lectured at which is a balance plenty of writers struggle to find no matter how long they have been at it.

  2365. Vivod iz zapoya na domy_hnmt

    Честно говоря, куча народу сталкивается. Каждые выходные одно и то же. В этом вопросе очень важно не заниматься самодеятельностью. Нашел нормальный вариант — вывод из запоя на дому. Ребята реально шарят. Если честно, жмите сюда чтобы узнать подробности — вывод из запоя на дому недорого [url=https://vyvod-iz-zapoya-na-domu-voronezh-kmp.ru]https://vyvod-iz-zapoya-na-domu-voronezh-kmp.ru[/url] Звоните пока не поздно, так как алкоголь — это яд. Сам так спасал брата.

  2366. Vivod iz zapoya na domy_alOa

    Слушай, соседи уже устали слушать эти крики. Без вариантов — круглосуточный вывод из запоя без отмазок. Ребята работают чисто. Между нами, смотрите сами по ссылке — нарколог на дом вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru]нарколог на дом вывод из запоя на дому[/url] Организм не резиновый. Поверьте моему опыту, чем труп из квартиры выносить. Проверенный вариант по городу.

  2367. DonBlime

    Decided to set a calendar reminder to revisit, and a stop at coastharborartisanexchange extended that revisit list, calendar entries for content are a level of commitment I rarely make but when I do they signal a higher regard than a simple bookmark and this site has earned that calendar tier of relationship from me today.

  2368. Gilbertatofs

    Reading this confirmed a hunch I had been carrying about the topic without having articulated it, and a stop at oliveorchardartisanexchange extended the confirmation, content that gives shape to fuzzy intuitions is doing the rare work of making private thoughts public and this site is providing that articulating service consistently for me lately.

  2369. alkoholizem_dtSn

    Dolga leta sem se boril sam. Potem pa sem izvedel za center in vse se je postavilo na svoje mesto. Govorim o odvajanju od alkohola pri strokovnjakih, ki res znajo pomagati. Veste, alkoholizem je bolezen, ne slabost. In kar je najpomembneje – lahko ostanete doma. Sam sem preveril celoten postopek in vse uradne informacije so na voljo na tej povezavi: Dr Vorobjev [url=zdravljenjealkoholizma.com]zdravljenjealkoholizma.com[/url]. Po prvem tednu sem začutil razliko.

    Če kogarkoli, ki ga imate radi ne ve, kam se obrniti – najboljša odločitev je poklicati. Držim pesti!

  2370. BillyRew

    Really grateful for content like this, it does not waste my time and it does not insult my intelligence either, and a quick look at swamptweed was the same, balanced respectful writing that makes a person feel welcome rather than rushed through pages of forced engagement just to keep clicking around.

  2371. KenObesy

    Reading this confirmed a hunch I had been carrying about the topic without having articulated it, and a stop at everydaycartstore extended the confirmation, content that gives shape to fuzzy intuitions is doing the rare work of making private thoughts public and this site is providing that articulating service consistently for me lately.

  2372. MichaelDrymn

    Just want to flag that this was useful and not bury the appreciation in caveats, and a look at itobout earned the same direct praise, recognising good work without hedging it with criticism is something I try to practice because over qualified compliments tend to read as backhanded and miss the point sometimes.

  2373. Melvinnessy

    Adding to the bookmarks now before I forget, that is how good this is, and a look at scopevoice confirmed the rest of the site is worth saving too, this is one of those rare finds that justifies the time spent searching the web for once which is a relief in the current environment.

  2374. DorianBaf

    Polished and informative without feeling overproduced, that is the sweet spot, and a look at humivy hit it again, you can tell when a site has been built with care versus thrown together for the sake of having something to put online and this is clearly the former approach taken by the team.

  2375. Brettcrugh

    Really appreciate the confidence to make a clear point rather than hedging everything, and a quick visit to honeycovevendorgallery maintained the same direct stance, writing that takes positions rather than equivocating is more useful even when the positions are debatable because at least the reader has something to react to clearly.

  2376. Billysag

    Reading this on a phone at a coffee shop and finding it perfectly suited to that context, and a stop at corlex continued the comfortable mobile experience, content that works across reading conditions without compromising on substance is increasingly important and this site has clearly thought about the whole reader experience here.

  2380. Piercedib

    Appreciate the practical examples, they made the abstract points easier to grasp, and a stop at tracesinger added more of the same, this site clearly understands that real examples beat empty theory every single time which is the mark of a writer who knows their audience well and respects their time.

  2382. Antoniogag

    Now feeling slightly more committed to my own careful reading practices having read this, and a stop at jamcall reinforced that commitment, content that models the kind of attention it deserves is content that calibrates the reader and this site has clearly raised my own bar for what to bring to good writing today.

  2385. Felixjoift

    Now recognising the specific pleasure of reading writing that shows real care for sentence shapes, and a look at tritonstyle extended that craft pleasure, sentence level writing quality is something most blog content ignores entirely and this site has clearly invested in the prose layer alongside the substance which is rare today.

  2386. alkoholizem_lspn

    Zdravo, ljudje. Preizkusil sem že vse mogoče. Ko gre za zdravljenje alkoholizma — veliko ljudi se muči v tišini. Prijatelj mi je pokazal en center, kjer imajo izkušnje. Govorim o zdravljenju po metodi dr. Vorobjeva. Vse podrobnosti in izkušnje drugih ljudi najdete tukaj: alkoholizem [url=www.alkoholizem-zdravljenje.com]alkoholizem[/url] Meni so res pomagali. Prvi korak je vedno najtežji. Ampak ko dobiš strokovno podporo — življenje dobi nov smisel. Več kot vredno je poskusiti. Ne obupajte!

  2387. Vivod iz zapoya na domy_gtki

    Сил уже нет, родственники на нервах. Руки опускаются. Проверенный вариант — адекватный вывод из запоя цены указаны. Ребята знают свое дело. Короче, там все по полочкам — стоимость вывода из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-bvc.ru]https://vyvod-iz-zapoya-na-domu-voronezh-bvc.ru[/url] Не ждите чуда. Лучше решить проблему сейчас, чем хоронить близкого. Очень советую эту контору.

  2388. Vivod iz zapoya na domy_wwOa

    Слушай, соседи уже устали слушать эти крики. Без вариантов — реальное выведение из запоя без кодировки. Ребята работают чисто. Между нами, нажимайте и читайте — вывод из запоя на дому круглосуточно [url=https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru]https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru[/url] Печень вообще молчит. Лучше один раз дернуться, чем труп из квартиры выносить. Рекомендую эту наркологическую клинику.

  2389. alkoholizem_tySn

    Dolga leta sem se boril sam. Potem pa sem dobil pravi nasvet in vse se je spremenilo. Govorim o ambulantnem zdravljenju alkoholizma pri strokovnjakih, ki res znajo pomagati. Veste, odvisnost od alkohola ni sramota. In kar je najpomembneje – lahko ostanete doma. Sam sem preveril celoten postopek in vse uradne informacije so na voljo na tej povezavi: odvisnost od alkohol [url=www.zdravljenjealkoholizma.com]odvisnost od alkohol[/url]. Meni so resnično pomagali.

    Če kogarkoli, ki ga imate radi potrebuje pomoč – najboljša odločitev je poklicati. Držim pesti!

  2390. Jaydentiz

    Reading this confirmed a hunch I had been carrying about the topic without having articulated it, and a stop at coppercoveartisanexchange extended the confirmation, content that gives shape to fuzzy intuitions is doing the rare work of making private thoughts public and this site is providing that articulating service consistently for me lately.

  2391. Allenjep

    Now considering whether the post would translate well into a different form, and a look at jewelcovecommercegallery suggested similar versatility, content that could move into other media without losing its substance is content that has been built around ideas rather than around format and this site reads as idea first throughout posts.

  2392. Patrickbep

    Really appreciate the absence of stock photos that have nothing to do with the content, and a quick visit to heliokindle maintained the same restraint, visual filler is a tell that the writing cannot stand on its own and the lack of it here suggests the team has confidence in their content quality alone.

  2394. alkoholizem_lrpa

    Že kar nekaj časa spremljam to temo. Ko sem prvič slišal za ambulantno zdravljenje alkoholizma po metodi Dr Vorobjev centra, sem bil skeptičen. Ampak ko sem prebral izkušnje anderen — moje mnenje se je obrnilo. Odvisnost od alkohola je strašna bolezen. In najhuje je, da ljudje se sramujejo prositi za pomoč. Zato vam želim pokazati vse tehnične podrobnosti in uradne informacije, ki so na voljo na tej povezavi: alkoholizem [url=https://www.alkoholizma-zdravljenje-si.com]alkoholizem[/url]. Na tej povezavi so odgovori na vsa vprašanja.

    Zdaj živim polno življenje brez alkohola. Če se soočate s podobno težavo — vzemite si čas in preberite. Srečno vsem na tej poti!

  2395. MarshallRub

    A welcome reminder that thoughtful writing still happens online, and a look at floracovecommerceatelier extended that reassurance, the modern web makes it easy to forget that careful writing exists and finding sites that practice it is a small antidote to the cynicism that builds up from too much exposure to algorithmic content.

  2396. Vivod iz zapoya na domy_upmt

    Представьте ситуацию, куча народу сталкивается. Ситуация аховая. В такой теме очень важно не слушать советы алконавтов из подворотни. Я нарыл инфу — выведение из запоя без госпитализации. Там работают толковые врачи. Короче, жмите сюда чтобы узнать подробности — вывод из запоя стоимость [url=https://vyvod-iz-zapoya-na-domu-voronezh-kmp.ru]https://vyvod-iz-zapoya-na-domu-voronezh-kmp.ru[/url] Звоните пока не поздно, потому что запой убивает почки и сердце. Настоятельно рекомендую.

  2397. Walterbah

    Most posts I read end up forgotten within a day but this one is sticking, and a look at dawnmeadowcommercegallery extended that lingering effect, content that survives the immediate moment of reading rather than evaporating is content with genuine retention quality and this site has been producing memorable pieces at a rate notable across my reading.

  2398. MatthewNup

    Definitely a recommend from me, anyone curious about the topic should check this out, and a look at mooncovemerchantgallery adds even more reason for that, the depth and quality combine to make this site one I will be pointing people toward whenever similar conversations come up over the months ahead at work or socially.

  2399. Austinspove

    Now feeling the small relief of finding writing that does not condescend, and a stop at mossharborcraftcollective extended that respect for readers, content that treats its audience as capable adults rather than as people to be managed produces a different reading experience and this site has clearly chosen the respectful approach across all pieces.

  2400. WendellHor

    A piece that suggested careful editing without showing the marks of the editing, and a look at tritonsloop continued that invisible polish, the best editing disappears into the prose and this site reads as having been edited with skill that does not announce itself which is the highest compliment I can offer any blog content.

  2401. Martinwrest

    The depth of coverage felt about right for the format, neither shallow nor overwhelming, and a look at frostbrookvendorfoundry kept that calibration going, getting the depth right for blog format is genuinely difficult because too shallow loses experts and too deep loses beginners but this site nailed it nicely which I really do appreciate.

  2402. Dallasnut

    Appreciate the practical examples, they made the abstract points easier to grasp, and a stop at gunlex added more of the same, this site clearly understands that real examples beat empty theory every single time which is the mark of a writer who knows their audience well and respects their time.

  2403. Bradenrom

    Quality work here, the post reads cleanly and the points stay focused throughout, and a stop at goodsflexstore kept the standard high, you can tell the writer cares about the final result rather than just hitting publish for the sake of having something new on the page to feed the search engines.

  2404. VincentFes

    Refreshing to find writing that does not try to manipulate the reader into clicking onto the next page through cliffhangers and forced engagement, and a stop at scarabvogue continued in the same respectful way, this is what reader first design actually looks like in practice rather than just in marketing copy that sounds nice.

  2406. Masonwhold

    Reading more of the archives is now on my plan for the weekend, and a stop at huskgenie confirmed the archive worth the time, the rare archive worth a dedicated reading session rather than just casual sampling is the rare archive of serious work and this site has clearly produced enough of that work to warrant the deeper exploration.

  2407. Tobiasdig

    A piece that read smoothly because the writer understood how readers actually move through prose, and a look at izoblade maintained the same reader awareness, writers who think about the reading experience as much as the writing experience produce better work and this site has clearly made that shift in editorial approach.

  2409. DanEsori

    Worth a quiet moment of recognition for the consistency I have noticed across multiple posts, and a stop at vyxarc continued that consistent quality, sites that maintain quality across many pieces rather than peaking on one viral post are sites with real editorial discipline and this one has clearly developed that discipline carefully.

  2410. Howardsox

    Skipped lunch to finish reading, which says something, and a stop at opalriverartisanexchange kept me at my desk longer than planned, when content beats the lunch impulse the writer has done something genuinely impressive in an attention environment full of immediately satisfying alternatives competing for the same finite block of reader time.

  2413. ColbyBuh

    Found the section structure particularly thoughtful, and a stop at serifsorbet suggested the same care across the broader site, structural choices guide the reader through the material in ways most people do not consciously notice but feel the absence of when those choices are made carelessly or not at all.

  2414. AlvinMeelt

    Recommend this to anyone who values clear thinking over flashy presentation, and a stop at jamkix continued in the same understated way, this site has its priorities in the right place which makes it worth supporting through repeat visits and recommendations rather than just one passing read today before moving on quickly elsewhere.

  2415. Vivod iz zapoya na domy_fuki

    Блин, родственники на нервах. Что делать — непонятно. Проверенный вариант — нормальное выведение из запоя капельницей. Не шарлатаны какие-то. Короче, тыкайте сюда — выведение из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-bvc.ru]выведение из запоя на дому[/url] Организм не вывозит. Сам через это прошел, чем потом собирать по кускам. Серьезно ребят.

  2416. Vivod iz zapoya na domy_raOa

    Нифига себе проблема, родственники маются. Как есть — реальное выведение из запоя без кодировки. Врачи с допуском. Между нами, смотрите сами по ссылке — вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru]вывод из запоя на дому[/url] Печень вообще молчит. Поверьте моему опыту, чем труп из квартиры выносить. Рекомендую эту наркологическую клинику.

  2417. alkoholizem_bapn

    Pozdravljeni. Že dolgo sem iskal resnično rešitev. Ko gre za ambulantno zdravljenje alkoholizma — ni šala. Prijatelj mi je svetoval en center, kjer ne obetajo nemogočega. Govorim o Dr Vorobjev. Vse podrobnosti in izkušnje drugih ljudi najdete tukaj: Dr Vorobjev [url=https://alkoholizem-zdravljenje.com]https://alkoholizem-zdravljenje.com[/url] Meni so res pomagali. Ni lahko priznati si, da imaš težavo. Ampak ko vidiš, da nisi sam — vse postane lažje. Vsekakor priporočam vsem, ki se spopadajo s to težavo. Srečno na tej poti!

  2419. Jimbop

    A piece that exhibited the kind of patience that good writing requires, and a look at reliableshoppinghub continued that patient quality, hurried writing is easy to spot and this site reads as having been written without time pressure which produces a different feel than the rushed content that dominates much of the modern blog space.

  2421. alkoholizem_nySn

    Že dolgo nisem vedel, kako naprej. Potem pa sem izvedel za center in vse se je spremenilo. Govorim o odvajanju od alkohola pri Dr Vorobjevu. Veste, alkoholizem je bolezen, ne slabost. In kar je najpomembneje – program je prilagojen posamezniku. Sam sem preveril celoten postopek in vse uradne informacije so na voljo na tej povezavi: zdravljenje alkoholizma [url=http://zdravljenjealkoholizma.com]zdravljenje alkoholizma[/url]. Po prvem tednu sem začutil razliko.

    Če nekdo v vaši okolici ne ve, kam se obrniti – resnično priporočam. Držim pesti!

  2422. Freddierup

    Thanks for the simple approach, too many sites bury the actual point under layers of unnecessary words, but here every line earns its place, and a look at nightorchardmerchantgallery showed the same care for the reader which is something I will remember the next time I need answers on a topic.

  2423. Vivod iz zapoya na domy_wumt

    Честно говоря, многие не знают как быть. Каждые выходные одно и то же. В такой теме очень важно не заниматься самодеятельностью. Я нарыл инфу — вывод из запоя на дому. Клиника с лицензией. Короче, жмите сюда чтобы узнать подробности — вывод из запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-voronezh-kmp.ru]https://vyvod-iz-zapoya-na-domu-voronezh-kmp.ru[/url] Промедление смерти подобно, потому что один финал — реанимация. Проверено на себе.

  2424. Terrybeaum

    Refreshing tone compared to the dry corporate posts on similar topics, and a stop at rivercovecraftcollective carried that personality through nicely, you can tell when a real person is behind the writing versus a content team chasing metrics and this site definitely falls into the former category clearly across what I have seen.

  2425. Mikezew

    Useful read, especially because the writer did not assume too much background from the reader, and a quick look at veilshrine continued in the same way, a thoughtful site that meets people where they are which is something the modern web could use a lot more of for both casual and serious readers.

  2426. DevantegoP

    Now appreciating that the post did not require me to agree with the writer to find it valuable, and a look at floraridgevendoratelier maintained the same useful regardless of agreement quality, content that informs even when it does not convince is content with broader utility and this site reads as useful even when I disagree.

  2427. Lawsonsmuth

    Reading this with a notebook open turned out to be the right move, and a stop at goldencovecraftcollective added more material to the notes, content that justifies active note taking from a passive reader is content with real informational density and this site is producing notes worthy material at a high rate consistently.

  2428. Tylershada

    Once you find a site like this the search for similar voices begins, and a look at opalmeadowcommercegallery extended the search energy, finding a high quality reference point makes the gap between it and adjacent sources visible in a way it was not before and this site has provided that high reference point across multiple recent visits.

  2430. Cooperqueni

    Speaking as someone who used to recommend blogs frequently and got out of the habit this site is rekindling that impulse, and a look at nightorchardartisanexchange extended the rekindling, the recovery of an old habit triggered by encountering work that justifies it is itself a small kind of pleasure and this site is providing that recovery experience.

  2431. StanleyExoca

    Granted I am giving this site more credit than I usually give new finds, and a look at driftwillowcommercegallery continued earning that credit, the calibration of how much trust to extend after limited exposure is something I do carefully and this site has earned more trust on shorter exposure than most due to consistent quality across.

  2432. shkola onlain_imki

    Кто устал от обычной школы Учителя которые только оценками меряют А эти бесконечные ремонты в классе Короче, школа где ребёнку комфортно — школа онлайн с лицензией и зачислением Учителя настоящие профи В общем, там программа и условия — online school [url=https://shkola-onlajn-bxf.ru]https://shkola-onlajn-bxf.ru[/url] Не мучайте себя и детей Перешлите другим родителям

  2433. Aidanrow

    Really appreciate that the writer did not assume I would read every other related post first, and a look at goodshubonline kept that self contained feel going where each piece can stand alone, accessibility for new readers is a sign of generous editorial thinking and this site has clearly invested in that approach.

  2434. alkoholizem_oipa

    Dolgo sem iskal pravo rešitev. Ko sem prvič slišal za ambulantno zdravljenje alkoholizma po metodi Dr Vorobjev centra, sem bil skeptičen. Ampak ko sem prebral izkušnje anderen — moje mnenje se je obrnilo. Alkoholizem uničuje družine. In najhuje je, da ne poznajo dobrih možnosti zdravljenja. Zato priporočam, da preverite celoten postopek na spletni strani, ki so na voljo na tej povezavi: ambulantno zdravljenje alkoholizma [url=https://www.alkoholizma-zdravljenje-si.com]https://www.alkoholizma-zdravljenje-si.com[/url]. Tam boste našli vse potrebne informacije.

    Po dolgih letih sem končno našel rešitev. Če vas to zanima — to je lahko prelomnica v vašem življenju. Upam, da vam bo koristilo!

  2435. BarryAmumb

    Different feel from the algorithmically optimised posts that dominate the topic, and a stop at daheko reinforced that human touch, you can tell when a site is being run by someone who reads what they publish versus someone just hitting submit and moving on quickly to the next assignment without checking the result.

  2436. JeromeTRURI

    Strong recommendation, anyone interested in this topic owes themselves a visit, and a stop at orchardharborcraftcollective extends that recommendation across more of the site, this is the kind of resource that makes me more optimistic about the state of the open web than I usually am these days actually for once which is genuinely refreshing.

  2437. Chadcef

    Adding to the bookmarks now before I forget, that is how good this is, and a look at storkumber confirmed the rest of the site is worth saving too, this is one of those rare finds that justifies the time spent searching the web for once which is a relief in the current environment.

  2439. Vivod iz zapoya na domy_hyki

    Блин, родственники на нервах. Что делать — непонятно. Наркологическая клиника с выездом — срочный вывод из запоя без лишних вопросов. Не шарлатаны какие-то. Короче, смотрите сами по ссылке — срочный вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-bvc.ru]срочный вывод из запоя[/url] Каждая пьянка минус ресурс. Сам через это прошел, чем хоронить близкого. Серьезно ребят.

  2440. Vivod iz zapoya na domy_dvOa

    Нифига себе проблема, человек просто в штопоре. Как есть — круглосуточный вывод из запоя без отмазок. Ребята работают чисто. Между нами, там все подробно расписано — откапаться на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru]https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru[/url] Печень вообще молчит. Лучше один раз дернуться, чем потом скорую вызывать. Проверенный вариант по городу.

  2441. PorterDyela

    However measured this site clears the bar I set for sites I take seriously, and a stop at digitalbuyarena continued clearing that bar, the metrics I use for site quality are admittedly informal but they are consistent and this site has cleared them on multiple measurements across multiple visits which is meaningful for my evaluation.

  2442. WarrenCLODS

    Found the use of subheadings really helpful for scanning back through the post later, and a stop at jamsyx kept that reader friendly approach going, navigation is something many blog writers ignore but small structural choices make a noticeable difference for someone returning to find a specific point again days or weeks later.

  2443. LoganFex

    Honest opinion is that this is the kind of post that builds long term trust with readers, and a look at japarrow reinforced that perception, the slow accumulation of trust through consistent quality is the only sustainable way to build a real audience and this site is clearly playing that long game.

  2444. BertramWoorb

    Reading this confirmed a small detail I had been uncertain about, and a stop at haclex provided the source for further checking, content that supports verification through citations or links rather than just asserting facts is more trustworthy and this site has clearly built its credibility through that kind of verifiable approach consistently.

  2445. Calebbeini

    Closed three other tabs to focus on this one and never opened them again, and a stop at helmkit similarly held attention exclusively, content that crowds out other reading from working memory is content with real density and this site has demonstrated that density across multiple pages I have visited so far this morning.

  2446. Reggiegog

    Now sitting back and recognising that this was a small but real win in my reading day, and a stop at tailorteal extended that quiet win, the cumulative effect of small reading wins versus the cumulative effect of small reading losses is real over time and this site is contributing to the wins side of that ledger.

  2447. gryzopodemnoe oborydovanie_tdmt

    Слушайте кто подъемники ищет Задолбался я уже оборудование подбирать То тельферы клинят Короче, нашел нормальных производителей — подъемное оборудование для производства любой сложности Цены ниже чем у перекупов на 20% В общем, там каталог и цены — лебедка электрическая [url=https://tal-elektricheskaya.ru]https://tal-elektricheskaya.ru[/url] Проверяйте производителя по документам Перешлите тому кто ищет оборудование

  2450. alkoholizem_vppn

    Zdravo, ljudje. Dolgo časa nisem vedel, kam naprej. Ko gre za zdravljenje alkoholizma — to je res težka zadeva. Prijatelj mi je svetoval en center, kjer imajo izkušnje. Govorim o Dr Vorobjev centru. Več informacij je na voljo tu: odvajanje od alkohola [url=www.alkoholizem-zdravljenje.com]odvajanje od alkohola[/url] Meni so res pomagali. Odvisnost od alkohola je bolezen, ne sramota. Ampak ko dobiš strokovno podporo — življenje dobi nov smisel. Če kdo dvomi, naj kar pokliče in vpraša. Srečno na tej poti!

  2451. Riverelume

    A clear case of writing that does not try to do too much in one post, and a look at turbineunion maintained the same scoped discipline, posts that try to cover too much end up covering nothing well and this site has clearly chosen scope discipline as a core editorial principle which shows up clearly in what I read.

  2452. CristianDep

    Really appreciate the lack of pop ups, modals, cookie banners stacking on top of each other, and a quick visit to vaultvelour confirmed the same clean approach across the rest of the site, technical decisions about user experience are part of what makes content actually pleasant to engage with for sure.

  2453. GlenGlype

    Reading this gave me the rare experience of fully agreeing with all the conclusions, and a stop at vyxbrisk continued that agreement pattern, content that aligns with my existing views without seeming designed to do so is just content that happens to be reasonable and this site reads as reasonable rather than ideological mostly.

  2455. Brandonsob

    The examples really helped me grasp the points faster than abstract descriptions would have, and a stop at maplecrestcraftcollective added a few more practical illustrations that drove the message home, the kind of writing that knows its readers learn better through concrete situations rather than vague generalities is rare and worth recognising clearly.

  2456. Kerrytar

    Reading this gave me material for a conversation I needed to have anyway, and a stop at taupeswift added even more talking points, content that connects to upcoming social or professional needs rather than just being interesting in the abstract is the kind that earns priority placement in my attention these days routinely.

  2457. Vivod iz zapoya na domy_ximt

    Представьте ситуацию, многие не знают как быть. Каждые выходные одно и то же. В этом вопросе главное не слушать советы алконавтов из подворотни. Посмотрите сами — вывод из запоя цены адекватные. Там работают толковые врачи. Если честно, вся инфа тут — вывод из запоя на дому недорого [url=https://vyvod-iz-zapoya-na-domu-voronezh-kmp.ru]https://vyvod-iz-zapoya-na-domu-voronezh-kmp.ru[/url] Звоните пока не поздно, потому что один финал — реанимация. Проверено на себе.

  2458. GregoryTok

    Honest reaction is that this is the kind of writing I would defend in a conversation about good blog content, and a look at valecovemerchantgallery reinforced that, the rare site whose work I would actively recommend rather than just tolerate is the kind I want to support through return visits regularly.

  2459. Keaganencof

    Reading this prompted me to subscribe to my first newsletter in months, and a stop at biabrook confirmed the subscribe was the right call, content that earns a newsletter signup is content that has cleared a higher trust bar than a casual visit and this site has clearly earned that level of commitment from me.

  2460. Ervinabumb

    A piece that did not lecture even when it had clear positions, and a look at jazfix maintained the same teaching without preaching tone, finding the line between informing and lecturing is hard and most sites land on the wrong side of it but this one has clearly figured out how to inform without becoming preachy.

  2461. FreddieJum

    A particular pleasure to read this with a fresh coffee, and a look at idozix extended the pleasure across more pages, content that pairs well with quiet morning rituals is something I have come to value highly and this site has the kind of energy that fits naturally into a calm reading routine.

  2462. Vivod iz zapoya na domy_kjEi

    Народ, попал в такую передрягу. Родственник пьет без остановки. Руки опускаются. Участковый только руками разводит. Короче, только это и работает — качественная наркологическая клиника на выезде. Поставили систему. В общем, вся информация вот здесь — сколько стоит вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-zqw.ru]сколько стоит вывод из запоя[/url] Промедление смерти подобно. Скиньте кому надо.

  2463. Vivod iz zapoya na domy_pool

    Народ, сталкивался сам с таким — муж пьёт без остановки. Соседи звонят в дверь. Участковый разводит руками. У меня брат так чуть не загнулся. Короче, только это и работает — лучшая наркологическая клиника с выездом. Поставили систему за 20 минут. В общем, сохраняйте себе на будущее — вывод из запоя стоимость [url=https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru]https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru[/url] Промедление реально убивает. Здоровье дороже. Перешлите тому кто в беде.

  2464. RoyHiedy

    Just one of those reads that left me feeling slightly more capable rather than overwhelmed, and a look at forestcovecommerceatelier kept that empowering feel going, the difference between content that builds the reader up and content that intimidates them is huge and this site clearly knows which side of that line to stand.

  2465. Vivod iz zapoya na domy_xhki

    Сил уже нет, родственники на нервах. Что делать — непонятно. Проверенный вариант — срочный вывод из запоя без лишних вопросов. Ребята знают свое дело. Короче, вот вам информация — помощь при запое на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-bvc.ru]https://vyvod-iz-zapoya-na-domu-voronezh-bvc.ru[/url] Каждая пьянка минус ресурс. Сам через это прошел, чем потом собирать по кускам. Проверено на своей шкуре.

  2466. Vivod iz zapoya na domy_dyOa

    Нифига себе проблема, родственники маются. Без вариантов — круглосуточный вывод из запоя без отмазок. Тут тебе не частная лавочка. Между нами, нажимайте и читайте — вывод из запоя цены воронеж [url=https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru]https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru[/url] Организм не резиновый. Лучше один раз дернуться, чем труп из квартиры выносить. Рекомендую эту наркологическую клинику.

  2467. Brycerer

    Now realising the post solved a small problem I had been carrying for weeks, and a look at orchardmeadowcommercegallery extended that problem solving function, content that connects to specific unresolved questions in my own life rather than just providing general interest is content with real practical impact and this site is providing that practical value.

  2468. AntonioAlusy

    Saving the link for sure, this one is a keeper, and a look at goodsroutestore confirmed I should bookmark the entire site rather than just this page, the consistency across what I have seen so far suggests there is a lot more here worth coming back for soon when I have more time.

  2469. Gradynob

    Reading this confirmed that my time researching the topic in other places had not been wasted, and a stop at oakcoveartisanexchange extended the confirmation, when independent sources agree that is a useful signal and this site is one of the more reliable sources I have found for cross checking what I read elsewhere on similar subjects.

  2470. Levisnoke

    Approaching this site through a casual link click and being surprised by what I found, and a look at pearlcovecraftcollective extended the surprise, the rare experience of stumbling into excellent independent content rather than predictable mediocrity is one of the actual remaining pleasures of casual web browsing and this site provided it cleanly.

  2471. Lylecoups

    Decided this was the kind of site I would defend in a discussion about good blog content, and a stop at triggersyrup reinforced that, very few sites earn active defence rather than passive consumption and this one has clearly crossed that threshold for me without needing any explicit pitch from the writers themselves either.

  2472. ErnestoAmeve

    Really appreciate the confidence to make a clear point rather than hedging everything, and a quick visit to graniteorchardcraftcollective maintained the same direct stance, writing that takes positions rather than equivocating is more useful even when the positions are debatable because at least the reader has something to react to clearly.

  2473. JuliusEmife

    Liked the way the post handled the final paragraph, no neat bow but no abrupt cutoff either, and a stop at echobrookmerchantgallery continued that thoughtful ending pattern, endings are hard and most blog writers either over engineer them or skip them entirely and this site has clearly figured out a sustainable middle approach.

  2474. DorianNof

    Glad the writer did not feel the need to argue with imaginary critics in the post itself, and a stop at shoptrailmarket kept the same focused approach going, defensive writing wastes the reader time and confidence on positions that did not need defending and this post has clearly avoided that common failure.

  2475. alkoholizem_enpa

    Veliko sem prebral in slišal o tem. Ko sem prvič slišal za ambulantno zdravljenje alkoholizma po metodi Dr Vorobjeva, sem bil skeptičen. Ampak ko sem prebral izkušnje anderen — ugotovil sem, da to res deluje. Vsak dan se veliko ljudi bori s to težavo. In najhuje je, da ne poznajo dobrih možnosti zdravljenja. Zato priporočam, da preverite celoten postopek na spletni strani, ki so na voljo na tej povezavi: ambulantno zdravljenje alkoholizma [url=http://alkoholizma-zdravljenje-si.com]http://alkoholizma-zdravljenje-si.com[/url]. Na tej povezavi so odgovori na vsa vprašanja.

    Zdaj živim polno življenje brez alkohola. Če vas to zanima — ne odlašajte. Vsak dan je nova priložnost.

  2476. CraigRaf

    Now feeling confident that this site will continue producing work I will want to read, and a look at syxblue extended that confidence into the future, projecting forward from current quality to expected future quality is something I do for sites I genuinely follow and this one has earned that forward looking trust clearly today.

  2477. ZaneSpick

    Liked that the post resisted a sales pitch ending, and a stop at trumpetsash maintained the no pitch approach, content that ends without trying to convert me into a customer or subscriber is content that has confidence in its own value and this site is clearly playing the long game on reader trust.

  2478. Jaydenneift

    Worth flagging this site to a few specific friends who would appreciate the editorial sensibility, and a look at buyedgeshop added more pages I will mention to them, recommending sites to specific people requires understanding both the site and the person and this site is making those personalised recommendations easy and natural for me.

  2479. WestonZenda

    Easily one of the better explanations I have read on the topic, and a stop at digitalgoodscorner pushed it even higher in my mental ranking of useful resources, the kind of site that beats the average not by trying harder but by simply caring more about what it puts out daily which always shows.

  2480. Rayexoms

    If you scroll past this site without looking carefully you will miss something, and a stop at jibion extended that mild warning, the surface of the site does not advertise its quality loudly which means careful attention is required to recognise what is being offered here which is itself a kind of editorial signal.

  2482. PrinceKib

    Generally I do not leave comments but this post merits a small note, and a stop at broblur extended that comment worthy quality, the urge to actively contribute to a sites community rather than passively consume from it is something specific content provokes and this site has provoked that engagement urge from me today.

  2483. Israelpaf

    Came away with a small but real shift in perspective on the topic, and a stop at hagaro pushed that shift a bit further, the kind of subtle reframing that good writing does to a reader without making a big deal of it is something I always appreciate when it happens which is sadly not that often.

  2484. BertZedge

    Going to come back when I have more time to read carefully, the post deserves more than a quick scan, and a stop at gorurn reinforced that, this is the kind of site that rewards a slower read which is hard to find in this fast paced corner of the internet but really worthwhile.

  2486. Vivod iz zapoya na domy_pmmt

    Знаете, многие не знают как быть. Ситуация аховая. В этом вопросе очень важно не заниматься самодеятельностью. Я нарыл инфу — вывод из запоя цены адекватные. Клиника с лицензией. Если честно, вся инфа тут — нарколог на дом вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-kmp.ru]нарколог на дом вывод из запоя на дому[/url] Звоните пока не поздно, так как алкоголь — это яд. Сам так спасал брата.

  2487. Vivod iz zapoya na domy_agki

    Ох уж это, каждое утро одно и то же. Что делать — непонятно. Наркологическая клиника с выездом — круглосуточный вывод из запоя и стабилизация. Ребята знают свое дело. Короче, тыкайте сюда — выведение из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-bvc.ru]выведение из запоя на дому[/url] Не ждите чуда. Лучше решить проблему сейчас, чем потом собирать по кускам. Проверено на своей шкуре.

  2488. Vivod iz zapoya na domy_lcOa

    Слушай, соседи уже устали слушать эти крики. Без вариантов — реальное выведение из запоя без кодировки. Ребята работают чисто. Между нами, смотрите сами по ссылке — стоимость вывода из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru]https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru[/url] Печень вообще молчит. Лучше один раз дернуться, чем труп из квартиры выносить. Проверенный вариант по городу.

  2489. Tonyham

    Now I want to find more sites like this but I suspect they are rare, and a look at marblecovecraftcollective extended that thought, the few sites that meet this quality bar are precious specifically because they are rare and finding others like them is one of the ongoing projects of careful internet curation across the years.

  2490. Vivod iz zapoya na domy_ytoi

    Народ кто сталкивался, ситуация просто аховая. Братан уже четвёртые сутки в штопоре. Думали конец. Скорая не приезжает. Короче, только это и спасло — профессиональная наркологическая клиника на выезде. Поставили систему. В общем, сохраняйте — откапаться на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-lnm.ru]https://vyvod-iz-zapoya-na-domu-voronezh-lnm.ru[/url] Не тяните резину. Перешлите другу.

  2491. Linwoodarige

    Liked the careful word choice throughout, every term seemed picked for a reason rather than thrown in casually, and a stop at sheentabby continued that precise style, this kind of attention to small details is what separates careful writing from the usual rushed content that dominates blog spaces today across pretty much every topic I follow.

  2492. Lewiscot

    Speaking carefully because I do not want to overstate things this site is genuinely above average across multiple measurements, and a stop at driftcovecommerceatelier continued the above average performance, the calibration of judgement against potential overstatement is something I take seriously and this site clears the higher bar even after that calibration applies.

  2493. Jaydendib

    Now thinking the topic is more interesting than I had given it credit for, and a stop at fernbrookvendorfoundry continued that elevated interest, content that revives my curiosity about subjects I had set aside is doing genuine work in the structure of my interests and this site is providing that revivifying effect today actually.

  2494. Vivod iz zapoya na domy_biEi

    Друзья, столкнулся с такой ситуацией. Близкий уже неделю не просыхает. Нервов ни у кого нет. Скорая не едет. Короче, только это и работает — качественная наркологическая клиника на выезде. Откачали за час. В общем, жмите чтобы не потерять — вывод из запоя на дому круглосуточно [url=https://vyvod-iz-zapoya-na-domu-voronezh-zqw.ru]https://vyvod-iz-zapoya-na-domu-voronezh-zqw.ru[/url] Не надейтесь на авось. Скиньте кому надо.

  2495. JakeFem

    Reading this in pieces over a coffee break and finding it consistently rewarding, and a stop at atticboulder extended that into related material I will return to later, the kind of site that fits naturally into small reading windows without requiring a long uninterrupted block is genuinely useful for how I actually browse.

  2496. Coryurgep

    Found this really helpful, the explanations are simple but they actually answer the questions a normal reader would have, and after I followed lemonridgecommercegallery I had a clearer sense of the topic, no extra fluff just useful points laid out in a sensible order that made the time worth it.

  2498. SkylarEnsut

    Well structured and easy to read, that combination is rarer than people think, and a stop at jebbeo confirmed the same standard runs across the rest of the site, definitely the kind of place I will be coming back to when this topic comes up in conversation later again over the weeks ahead.

  2499. Vivod iz zapoya na domy_pbol

    Ребята, сталкивался сам с таким — муж пьёт без остановки. Жена в слезах. А скорая не едет. Я через это прошёл. Короче, только это и работает — лучшая наркологическая клиника с выездом. Примчались за час. В общем, смотрите сами по ссылке — выведение из запоя на дому воронеж [url=https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru]https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru[/url] Не тяните резину. Здоровье дороже. Перешлите тому кто в беде.

  2500. OtisLor

    Strong recommendation from me, anyone curious about the topic should make time for this, and a look at forestcovegoodsatelier only sharpens that recommendation further, the kind of resource that holds up against careful scrutiny rather than crumbling at the first critical question is rare and worth pointing other people toward when the topic comes up.

  2501. Eddiefak

    Solid quality, the kind of work that holds up to a careful read rather than a quick skim, and a quick look at igogoa kept that standard going strong, content that rewards attention rather than punishing it is something I appreciate more and more these days online across nearly every topic I follow.

  2502. DavionFromo

    Just want to flag that this was useful and not bury the appreciation in caveats, and a look at goodswaystore earned the same direct praise, recognising good work without hedging it with criticism is something I try to practice because over qualified compliments tend to read as backhanded and miss the point sometimes.

  2503. Taylornog

    The depth of coverage felt about right for the format, neither shallow nor overwhelming, and a look at targetskein kept that calibration going, getting the depth right for blog format is genuinely difficult because too shallow loses experts and too deep loses beginners but this site nailed it nicely which I really do appreciate.

  2504. Carldap

    Reading this in a relaxed evening setting was a small pleasure, and a stop at oakcovecraftcollective extended the pleasant evening reading, content that fits the tone of relaxed time without becoming forgettable is what I look for in evening reading and this site has the right tone for that particular slot in my daily reading routine.

  2505. Pedrolaurb

    Such writing is increasingly rare and worth supporting through attention, and a stop at pebblepinemerchantgallery extended that supportive attention across more pages, the conscious choice to spend time on sites that produce careful work rather than convenient consumption is itself a small form of patronage and this site is receiving that conscious patronage from me.

  2507. RiverPek

    Even on a quick first read the substance of the post comes through, and a look at vincatrench reinforced that immediate quality, content that does not require a slow careful read to demonstrate value but rewards one anyway is content with real depth and this site has produced work of that demanding depth class.

  2508. MalcolmHon

    Beyond the topic at hand this site reads as a small ongoing project of taking writing seriously, and a look at brofix reinforced that project quality, sites that treat publishing as an ongoing serious practice rather than as content production for traffic are sites worth supporting and this one has clearly chosen the serious approach.

  2509. CarmineScoms

    Picked this for a morning recommendation in our company chat, and a look at vyxcar suggested I will mention this site again later, recommending content into a workplace context is a small editorial act that requires confidence in the recommendation and this site is making me confident in those recommendations consistently here too.

  2510. Landonhax

    Considered as a whole this site has developed a coherent point of view that comes through in individual pieces, and a look at emberstonecommercegallery continued displaying that coherence, sites with a unified perspective rather than a grab bag of takes are sites with editorial maturity and this one has clearly developed that maturity through years of work.

  2511. Landonsmeni

    Halfway through I knew I would finish the post, and a stop at hazelharborcraftcollective also held me through to the end, content that signals its quality early and then sustains it is content with real internal consistency and this site has clearly figured out how to maintain quality from opening sentence through to closing thought.

  2512. GordonCoomo

    Worth recognising that the post did not pretend to be the final word on the topic, and a stop at fastcartsolutions continued that humility, content that admits its own scope and limits is more trustworthy than content that overreaches and this site has clearly developed the editorial maturity to know what it can and cannot claim well.

  2513. alkoholizem_zopa

    Veliko sem prebral in slišal o tem. Ko sem prvič slišal za ambulantno zdravljenje alkoholizma po metodi Dr Vorobjeva, sem bil poln dvomov. Ampak ko sem spoznal ljudi, ki jim je uspelo — moje mnenje se je obrnilo. Vsak dan se veliko ljudi bori s to težavo. In najhuje je, da ljudje se sramujejo prositi za pomoč. Zato priporočam, da preverite celoten postopek na spletni strani, ki so na voljo na tej povezavi: zdravljenje alkoholizma [url=alkoholizma-zdravljenje-si.com]zdravljenje alkoholizma[/url]. Tam boste našli vse potrebne informacije.

    Po dolgih letih sem končno našel rešitev. Če se soočate s podobno težavo — vzemite si čas in preberite. Upam, da vam bo koristilo!

  2514. Vivod iz zapoya na domy_vrOa

    Да уж, родственники маются. Без вариантов — адекватный вывод из запоя цены и условия. Ребята работают чисто. Короче говоря, нажимайте и читайте — цены на вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru]https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru[/url] Хватит надеяться на авось. Поверьте моему опыту, чем потом скорую вызывать. Проверенный вариант по городу.

  2515. Vivod iz zapoya na domy_yzki

    Ох уж это, родственники на нервах. Что делать — непонятно. Проверенный вариант — нормальное выведение из запоя капельницей. Не шарлатаны какие-то. Короче, смотрите сами по ссылке — вывод из запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-voronezh-bvc.ru]вывод из запоя на дому цена[/url] Организм не вывозит. Лучше решить проблему сейчас, чем хоронить близкого. Очень советую эту контору.

  2516. Vivod iz zapoya na domy_fwmt

    Знаете, многие не знают как быть. Ситуация аховая. В этом вопросе главное не заниматься самодеятельностью. Посмотрите сами — срочный вывод из запоя. Клиника с лицензией. Короче, жмите сюда чтобы узнать подробности — снятие запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-kmp.ru]https://vyvod-iz-zapoya-na-domu-voronezh-kmp.ru[/url] Звоните пока не поздно, потому что алкоголь — это яд. Проверено на себе.

  2517. SergioGob

    Just want to acknowledge that the writing here is doing something right, and a quick visit to nextcartstation confirmed the same standards run across the broader site, recognising good work is something I try to do when I find it because the alternative is silence and silence rewards mediocrity.

  2518. Vivod iz zapoya na domy_jioi

    Блин народ, столкнулись с жестью. Родственник просто пропадает. Руки опустились. В платную клинику денег нет. Короче, единственное что реально помогло — нормальное выведение из запоя капельницей. Отошёл за полчаса. В общем, вся инфа вот тут — снять запой на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-lnm.ru]https://vyvod-iz-zapoya-na-domu-voronezh-lnm.ru[/url] Не тяните резину. Сохраните себе.

  2519. NealVip

    However measured this site clears the bar I set for sites I take seriously, and a stop at halarch continued clearing that bar, the metrics I use for site quality are admittedly informal but they are consistent and this site has cleared them on multiple measurements across multiple visits which is meaningful for my evaluation.

  2520. Vivod iz zapoya na domy_tiEi

    Слушайте, попал в такую передрягу. Близкий уже неделю не просыхает. Думал уже всё. В больницу тащить страшно. Короче, единственное что реально помогло — профессиональный вывод из запоя на дому. Поставили систему. В общем, смотрите сами по ссылке — помощь вывода запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-zqw.ru]https://vyvod-iz-zapoya-na-domu-voronezh-zqw.ru[/url] Промедление смерти подобно. Скиньте кому надо.

  2521. FrederickTen

    Thanks for the simple approach, too many sites bury the actual point under layers of unnecessary words, but here every line earns its place, and a look at vergetrophy showed the same care for the reader which is something I will remember the next time I need answers on a topic.

  2522. Forestbed

    A clear cut above the usual noise on the subject, and a look at salemsolid only made that gap wider in my view, the kind of place that earns its visitors through quality rather than through aggressive marketing or sponsored placements which is increasingly the only way most sites stay afloat across the modern web.

  2523. Wesleyron

    Now realising the topic deserved better treatment than it has been getting elsewhere, and a look at meadowharborartisanexchange extended that broader recognition, content that exposes the gap between actual quality and average quality elsewhere is doing the quiet work of raising standards and this site is contributing to that elevation in its own corner.

  2524. ShawnHiedo

    Really appreciate that the writer did not assume I would read every other related post first, and a look at smartbuyingzone kept that self contained feel going where each piece can stand alone, accessibility for new readers is a sign of generous editorial thinking and this site has clearly invested in that approach.

  2526. Marloncrulk

    Started reading and ended an hour later without realising the time had passed, and a look at quickharborartisanexchange produced the same time dilation effect, when content makes time feel different the writer has achieved something well beyond the average and this site is producing that experience for me reliably across multiple readings.

  2527. Mosesgen

    A small thing but the line spacing and font choices made reading this physically pleasant, and a look at calicofalcon maintained the same careful design, technical choices about typography are part of what makes online reading actually comfortable and this site has clearly invested in the design layer alongside the content layer carefully.

  2528. DonnyMuh

    Easy to recommend, the content speaks for itself without needing additional praise from me, and a stop at linenmeadowcommercegallery only adds more reasons to send people this way, the kind of generous resource that benefits its readers without demanding anything in return is increasingly rare and worth recognising clearly today across the broader open internet.

  2529. Vivod iz zapoya na domy_ihol

    Товарищи, сталкивался сам с таким — близкий совсем не выходит из штопора. Жена в слезах. Участковый разводит руками. У меня брат так чуть не загнулся. Короче, только это и работает — качественный вывод из запоя на дому. Примчались за час. В общем, там контакты и прайс и условия — помощь вывода запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru]https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru[/url] Не надейтесь на авось. Здоровье дороже. Перешлите тому кто в беде.

  2530. ReneALlon

    Once I trust a site this much I tend to read everything they publish and that is the trajectory I am on with this one, and a stop at frostcovecommerceatelier confirmed the trajectory, the rare progression from interested reader to comprehensive reader is something only certain sites earn and this one is earning that progression rapidly.

  2531. Jasonabats

    Reading this prompted me to clean up some old notes related to the topic, and a stop at byncane extended that organising urge, content that triggers personal organisation rather than just consuming attention is content with motivating energy and this site has the kind of clarity that prompts active follow up rather than passive consumption.

  2532. QuentinrurOf

    Came away with some new perspectives I had not considered before, and after gadblow those ideas felt more complete, the kind of content that stays with you a little while after reading rather than slipping out the moment you switch tabs and move on with your day to whatever comes next.

  2533. Eduardomoock

    Useful enough to recommend to several people I know who would appreciate it, and a stop at homeneedsonline added more material I will pass along too, the kind of writing that earns word of mouth is the kind that actually delivers on its promises which is what this site does without any drama or fanfare attached.

  2534. Avinuage

    Quietly enjoying that I have found a new site to follow for the topic, and a look at trebleupper reinforced the small pleasure of the find, the discovery of new high quality sources is one of the more durable pleasures of careful internet reading and this site has been generating that discovery pleasure at multiple points already today.

  2535. TateEpisk

    A genuinely unexpected highlight of my reading week, and a look at ilefix extended that pattern, the surprise of finding excellent content rather than the predictable mediocre is one of the few real pleasures of casual web browsing and this site delivered that surprise cleanly today which I really do appreciate.

  2536. YorkFus

    Started reading without much expectation and ended on a high note, and a look at bitternarbor continued that arc, content that builds rather than peaks early is a sign of a writer who knows how to structure a piece for sustained reader engagement rather than relying on a strong hook to do all the work.

  2537. FidelLycLe

    Genuinely glad I clicked through to read this rather than skipping past, and a stop at cloudbrookvendorfoundry confirmed I should keep clicking through to more pages here, the kind of resource that justifies its place in my browser history rather than feeling like wasted time which is the highest compliment I offer any site online today.

  2538. Samueljorie

    Looking at the surface design and the substance together this site has both right, and a look at jebbird reinforced that integrated quality, sites where presentation and content reinforce each other rather than fighting are sites with full editorial coherence and this one has clearly invested in both layers in a balanced way.

  2539. Vivod iz zapoya na domy_flOa

    Нифига себе проблема, родственники маются. Без вариантов — только срочный вывод из запоя. Тут тебе не частная лавочка. Короче говоря, смотрите сами по ссылке — вывод из запоя цены воронеж [url=https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru]https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru[/url] Печень вообще молчит. Лучше один раз дернуться, чем труп из квартиры выносить. Рекомендую эту наркологическую клинику.

  2540. Vivod iz zapoya na domy_phki

    Ох уж это, человек просто не просыхает. Что делать — непонятно. Наркологическая клиника с выездом — срочный вывод из запоя без лишних вопросов. Не шарлатаны какие-то. Короче, тыкайте сюда — стоимость вывода из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-bvc.ru]https://vyvod-iz-zapoya-na-domu-voronezh-bvc.ru[/url] Не ждите чуда. Лучше решить проблему сейчас, чем потом собирать по кускам. Очень советую эту контору.

  2541. RyanHow

    Refreshing change from the usual sites covering this topic, no clickbait and no padding, and a stop at pineharborcommercegallery confirmed the difference, this place clearly has its own voice rather than copying the formulas everyone else uses to chase clicks online which is becoming increasingly rare these days across nearly every popular subject.

  2542. Tommyver

    The use of plain language without dumbing down the topic was really well done, and a look at gribrew continued in that same accessible style, this is something many technical writers fail at because they either confuse their readers or condescend to them but here neither problem appears at all which is impressive really.

  2543. Rayexoms

    Quietly enjoying that I have found a new site to follow for the topic, and a look at jibion reinforced the small pleasure of the find, the discovery of new high quality sources is one of the more durable pleasures of careful internet reading and this site has been generating that discovery pleasure at multiple points already today.

  2544. BillyDag

    Really appreciate the confidence to make a clear point rather than hedging everything, and a quick visit to goodsparkstore maintained the same direct stance, writing that takes positions rather than equivocating is more useful even when the positions are debatable because at least the reader has something to react to clearly.

  2545. KentonNup

    More original than the recycled takes I keep finding on the topic elsewhere, and a quick look at ivoryridgecraftcollective confirmed it, the kind of site that has its own voice rather than echoing whatever is trending which makes it stand out as a refreshing change from the usual rotation of generic content I see daily.

  2546. Vivod iz zapoya na domy_zroi

    Всем привет, ситуация просто аховая. Отец не вылезает из бутылки. Нервов уже ни у кого нет. В бесплатную тащить страшно — поставят на учёт. Короче, единственное что реально помогло — срочный вывод из запоя круглосуточно. Через час были. В общем, смотрите сами по ссылке — выведение из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-lnm.ru]выведение из запоя на дому[/url] Не ждите. Сохраните себе.

  2547. Vivod iz zapoya na domy_tzEi

    Ребята, бывает же такое горе. Человек просто в штопоре. Нервов ни у кого нет. Скорая не едет. Короче, единственное что реально помогло — качественная наркологическая клиника на выезде. Приехали. В общем, смотрите сами по ссылке — вывод из запоя на дому телефоны [url=https://vyvod-iz-zapoya-na-domu-voronezh-zqw.ru]https://vyvod-iz-zapoya-na-domu-voronezh-zqw.ru[/url] Не надейтесь на авось. Скиньте кому надо.

  2549. Bartholomewenlig

    Got something practical out of this that I can apply later this week, and a stop at vitalsummit added more details to think about, this is exactly the kind of content I bookmark for future reference rather than the throwaway listicles that dominate most search results these days for almost any common topic.

  2550. KrisUnign

    Now planning to write about the topic myself eventually using this post as a reference, and a look at siriustender would also serve in that future piece, content that becomes raw material for my own writing rather than just informing my reading is content with multiplicative value and this site is generating that multiplicative effect.

  2551. Cassidybet

    Yesterday I was complaining about the state of online writing and today this site has temporarily fixed that complaint, and a look at coppercovecraftcollective extended that mood reversal, the short term mood improvement that comes from finding good content is real and this site has produced that improvement for me at a useful moment.

  2552. PiercelAx

    Speaking as someone who reads a lot on this topic this site has earned a high position in my source rankings, and a stop at meadowharborcraftcollective reinforced that ranking, the informal ranking of sources for a topic is something I maintain mentally and this site has moved into the upper portion of those rankings clearly.

  2553. Jamesglync

    Just sat back at the end of the post and felt grateful that someone took the time to write it, and a look at buynestshop extended that gratitude across more of the site, recognising effort behind quality work is part of what makes the open web a community rather than just a marketplace today.

  2554. Mikemak

    Now feeling confident that this site will continue producing work I will want to read, and a look at hewblob extended that confidence into the future, projecting forward from current quality to expected future quality is something I do for sites I genuinely follow and this one has earned that forward looking trust clearly today.

  2555. HankAbaks

    Quietly building a case in my head for why this site deserves more attention than it currently seems to receive, and a look at wyxburn reinforced the case, the gap between quality and recognition is a recurring frustration in independent online content and this site is one of the cases that seems particularly egregious to me today.

  2557. Kadecak

    Quietly the writers approach to the topic differs from the dominant takes I have been encountering, and a stop at quickharborcraftcollective extended that distinctive approach, content that maintains a different perspective without explicitly arguing against the dominant ones is content with confident editorial identity and this site has that confidence throughout pieces.

  2558. Robertpoove

    Honest assessment is that this is one of the better short reads I have had this week, and a look at cadbrisk reinforced that, the bar for short content is low because most of it sacrifices substance for brevity but this site manages both at once which is harder than it sounds for most writers attempting it.

  2559. Vivod iz zapoya na domy_rtki

    Сил уже нет, человек просто не просыхает. Что делать — непонятно. Проверенный вариант — срочный вывод из запоя без лишних вопросов. Не шарлатаны какие-то. Короче, вот вам информация — вывести из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-bvc.ru]вывести из запоя на дому[/url] Не ждите чуда. Лучше решить проблему сейчас, чем хоронить близкого. Очень советую эту контору.

  2560. Lesterovato

    Now noticing how rare it is to find a site that does not feel rushed, and a look at swiftvantage extended that calm pace, content produced without time pressure has a different quality than content shipped to meet a deadline and this site reads as written without urgency which produces a different and better experience for readers.

  2561. Marcustix

    Decided this was the best thing I had read all morning, and a stop at sundaestudio kept that ranking intact, ranking my reading is something I do mentally throughout the day and the top rank is competitive and not easily won but this site won it without needing to overstate its claims for that.

  2562. Dexterkaf

    Now wishing more sites covered topics with this level of care, and a look at maplecrestmerchantgallery extended that wish across more subjects, the rarity of careful coverage on most topics is a problem and this site is one of the small antidotes to that broader pattern of casual or surface treatment of complex subjects.

  2563. Vivod iz zapoya na domy_gkol

    Товарищи, сталкивался сам с таким — муж пьёт без остановки. Жена в слезах. А скорая не едет. Сам был в такой жопе. Короче, только это и работает — адекватный вывод из запоя цены нормальные. Примчались за час. В общем, жмите чтобы не потерять — вывод из запоя на дому недорого [url=https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru]https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru[/url] Не тяните резину. Здоровье дороже. Перешлите тому кто в беде.

  2564. FrancisKab

    Just sat with this for a bit longer than I usually would because the points are worth thinking about, and after onecartplace I had even more to chew on, the kind of post that nudges your thinking forward without forcing the issue is something I have always appreciated in good writing online.

  2565. TimLes

    Reading this on a slow Sunday and finding it perfectly suited to a slow Sunday read, and a quick stop at ferncovevendorcorner kept the same gentle pace, content that fits the mood of the moment is something I notice and remember and this site has the kind of pace that suits relaxed reading sessions especially well.

  2566. VernonCoits

    Thanks for the honest framing without exaggerated claims that the topic will change my life, and a stop at ilenub kept the same modest tone, restraint in marketing language signals trustworthiness and the writers here are clearly playing the long game by building credibility rather than chasing immediate clicks through hyperbole.

  2567. Vivod iz zapoya na domy_rjOa

    Да уж, человек просто в штопоре. Как есть — адекватный вывод из запоя цены и условия. Ребята работают чисто. Между нами, вот нормальный расклад — откапаться на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru]https://vyvod-iz-zapoya-na-domu-voronezh-xrt.ru[/url] Печень вообще молчит. Поверьте моему опыту, чем потом скорую вызывать. Проверенный вариант по городу.

  2568. alkoholizem_zwpa

    Dolgo sem iskal pravo rešitev. Ko sem prvič slišal za ambulantno zdravljenje alkoholizma po metodi Dr Vorobjev centra, sem bil neveren. Ampak ko sem videl rezultate — moje mnenje se je obrnilo. Vsak dan se veliko ljudi bori s to težavo. In najhuje je, da ljudje se sramujejo prositi za pomoč. Zato vam želim pokazati vse tehnične podrobnosti in uradne informacije, ki so na voljo na tej povezavi: alkoholizem [url=https://alkoholizma-zdravljenje-si.com]alkoholizem[/url]. Več o tem si preberite na spodnji povezavi.

    Zdaj živim polno življenje brez alkohola. Če se soočate s podobno težavo — to je lahko prelomnica v vašem življenju. Upam, da vam bo koristilo!

  2569. Samgaf

    Most of my reading time goes to a small number of trusted sources and this one is now joining that group, and a stop at ravengrovecommercegallery reinforced the group membership, the few sites that earn a place in my regular rotation are sites I expect ongoing returns from and this one has earned that elevated position consistently.

  2570. NedLasty

    Definitely returning here, that is decided, and a look at jebmug only made the case stronger, this is one of those rare websites that rewards regular visits rather than feeling stale after the first read which is something I cannot say about most of the places I bookmark today across all my topics.

  2571. LelandTwive

    This stands out compared to similar posts I have read recently, less noise and more substance, and a look at ferncovemerchantgallery kept that gap going, you can really feel the difference between content made by someone who cares versus content made to fill a publishing schedule for an algorithm trying to keep growing somehow.

  2572. CadenTrush

    Better than the average post on this subject by some distance, and a look at flintbrookmarketfoundry reinforced that, you can tell within the first paragraph that the writer here actually cares about the topic rather than just covering it for the sake of having something to publish that week or that day.

  2573. AxelCon

    Bookmark added with a small mental note that this is a site to keep, and a look at cameogrouse reinforced the keep status, the verb keep rather than visit captures something about how I think about this kind of site and it is a higher tier of relationship than I have with most places online today.

  2574. Vivod iz zapoya na domy_lkmt

    Честно говоря, многие не знают как быть. Каждые выходные одно и то же. В этом вопросе очень важно не слушать советы алконавтов из подворотни. Посмотрите сами — выведение из запоя без госпитализации. Ребята реально шарят. Короче, актуальный прайс и условия тут — вывод из запоя цена [url=https://vyvod-iz-zapoya-na-domu-voronezh-kmp.ru]https://vyvod-iz-zapoya-na-domu-voronezh-kmp.ru[/url] Звоните пока не поздно, так как запой убивает почки и сердце. Проверено на себе.

  2575. Samsonfueta

    Closed the tab and immediately reopened it ten minutes later because I wanted to reread a part, and a stop at acornharborcommercegallery drew the same return, content that pulls you back after closing it is doing something well beyond the average and worth marking as exceptional in my mental catalogue of reliable sites.

  2576. Vivod iz zapoya na domy_bdoi

    Блин народ, столкнулись с жестью. Братан уже четвёртые сутки в штопоре. Руки опустились. В платную клинику денег нет. Короче, только это и спасло — профессиональная наркологическая клиника на выезде. Отошёл за полчаса. В общем, смотрите сами по ссылке — вывод из запоя цена на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-lnm.ru]https://vyvod-iz-zapoya-na-domu-voronezh-lnm.ru[/url] Не тяните резину. Сохраните себе.

  2577. TerrenceIdoft

    This filled in a gap in my understanding that I had not even noticed was there, and a stop at openmarketcart did the same, the kind of post that gives you more than you expected when you first clicked through from somewhere else, a real find for anyone curious about the area covered here.

  2578. Vivod iz zapoya na domy_lwEi

    Слушайте, попал в такую передрягу. Родственник пьет без остановки. Руки опускаются. Участковый только руками разводит. Короче, врачи толковые попались — срочный вывод из запоя круглосуточно. Поставили систему. В общем, жмите чтобы не потерять — сколько стоит вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-zqw.ru]сколько стоит вывод из запоя[/url] Промедление смерти подобно. Сохраните себе.

  2579. TatePlarf

    Genuine reaction is that I will probably think about this on and off for a few days, and a look at vesselthrift added fuel to that, the best content lingers in your head after you close the tab rather than evaporating immediately and this site clearly knows how to write that kind of memorable content.

  2580. EmerySab

    Liked that the post resisted a sales pitch ending, and a stop at bexedge maintained the no pitch approach, content that ends without trying to convert me into a customer or subscriber is content that has confidence in its own value and this site is clearly playing the long game on reader trust.

  2581. Kanerot

    I really like how the writer keeps the tone friendly without sounding fake or overly polished, and after a stop at crowncoveartisanexchange the same calm pace was there, no rushing to make a point and no padding either, just clean honest writing that I can respect and come back to later again.

  2582. Levihex

    I really like the calm tone here, it does not push anything on the reader, and after I went through mintorchardartisanexchange I felt the same way, just steady useful content laid out without drama, which is exactly what someone trying to learn something quickly needs to find rather than aggressive marketing.

  2583. Leeagemn

    Most attempts at writing on this topic feel like they are missing something and this post finally identified what was missing, and a look at humbust extended that diagnostic clarity, content that names what is wrong with adjacent treatments while doing better itself is content with both critical and constructive value and this site has both.

  2584. BrysonVox

    Comfortable read, finished it without realising how much time had passed, and a look at twisttailor pulled me into more pages the same way, the absence of friction in good content lets time disappear and that is one of the highest compliments I can pay any piece of writing I find online during a regular search session.

  2585. Sandybat

    Found a couple of useful angles in here I had not considered before reading carefully, and a quick stop at rainharborartisanexchange added more, this is one of those sites where the value compounds the more you read rather than peaking at one viral post and then offering nothing else of substance afterwards which is common.

  2586. Ronnieununc

    A particular kind of restraint shows up in the writing, and a look at cobqix maintained the same restraint across pages, knowing what not to say is just as important as knowing what to say and this site has clearly developed strong instincts on both sides of that editorial line throughout pieces I have read.

  2587. Morrislag

    Generally I bookmark sparingly to avoid building up a bookmark graveyard but this one earned a permanent slot, and a stop at infinitygoodscorner extended that permanence designation, the few sites I keep permanent bookmarks for are sites I expect to use repeatedly and this one has clearly cleared that expectation bar today.

  2588. CameronRot

    Now planning to share the link with a small group of readers I trust, and a look at citrinefjord suggested more material to share with the same group, recommending content into a curated circle requires confidence in the recommendation and this site is making me confident in those personal recommendations on multiple separate occasions now.

  2589. FletcherPayof

    Over the course of reading several posts here a pattern of quality has emerged, and a stop at stoneharborvendorparlor2 confirmed the pattern, the difference between sites that hit quality occasionally and sites that hit it consistently is huge and this site has clearly demonstrated the consistent kind through what I have read this morning.

  2590. Vivod iz zapoya na domy_viki

    Блин, родственники на нервах. Что делать — непонятно. Проверенный вариант — адекватный вывод из запоя цены указаны. Там реальные врачи. Короче, там все по полочкам — вывод из запоя круглосуточно [url=https://vyvod-iz-zapoya-na-domu-voronezh-bvc.ru]вывод из запоя круглосуточно[/url] Организм не вывозит. Лучше решить проблему сейчас, чем хоронить близкого. Серьезно ребят.

  2591. Elliotspire

    Now realising this site has been quietly doing good work for longer than I knew, and a look at saltvinca suggested an archive worth exploring, sites with deep archives of consistent quality represent a different kind of resource than sites with viral hits and this one looks like the durable kind based on what I see.

  2592. AronLar

    Reading this with a notebook open turned out to be the right move, and a stop at quickbuyershub added more material to the notes, content that justifies active note taking from a passive reader is content with real informational density and this site is producing notes worthy material at a high rate consistently.

  2593. NikoBlino

    Now wishing more sites covered topics with this level of care, and a look at jifaero extended that wish across more subjects, the rarity of careful coverage on most topics is a problem and this site is one of the small antidotes to that broader pattern of casual or surface treatment of complex subjects.

  2594. GrahamviP

    Adding to the bookmarks now before I forget, that is how good this is, and a look at maplegrovecommercegallery confirmed the rest of the site is worth saving too, this is one of those rare finds that justifies the time spent searching the web for once which is a relief in the current environment.

  2595. Vivod iz zapoya na domy_raol

    Ребята, представляете кошмар — отец просто умирает на глазах. Дети плачут. Участковый разводит руками. Сам был в такой жопе. Короче, только это и работает — лучшая наркологическая клиника с выездом. Поставили систему за 20 минут. В общем, вся инфа вот здесь — цены на вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru]https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru[/url] Не тяните резину. Деньги потом не нужны будут. Перешлите тому кто в беде.

  2596. Melvinsassy

    Reading this in a moment of low energy still kept my attention, and a stop at flintcovecommerceatelier continued that engagement under suboptimal conditions, content that survives the reader being tired is content with extra reserves of pull and this site has the kind of writing that holds up even when I am not at my reading best.

  2597. PhillipJerve

    Liked the post enough to read it twice and the second read found new things, and a stop at jebbrood similarly rewarded the second look, content with hidden depths that only reveal themselves on careful rereading is the rare kind that earns lasting respect rather than fleeting first impressions only briefly held.

  2598. Timmytus

    My professional context would benefit from having this kind of resource available, and a look at cobblebuckle extended the professional applicability, the rare site that contributes meaningfully to professional work rather than just personal interest is content with multiplied value and this one is providing that professional utility consistently across multiple pieces.

  2599. MelvinBug

    Picked this site to mention to a colleague who would benefit, and a look at rosecovemerchantgallery added more material I will pass along, recommending sites to colleagues is a higher bar than recommending to friends because the professional context demands more careful curation and this site cleared the professional bar without me having to think.

  2600. RudolphHap

    Felt this in a way I cannot quite explain, the topic just hit different here, and a stop at allthingsstore continued in that vein, sometimes you find a site whose perspective lines up with how you have been thinking and reading their work feels like a small relief which I appreciated more than I expected.

  2601. Vivod iz zapoya na domy_gfoi

    Блин народ, такая херня приключилась. Братан уже четвёртые сутки в штопоре. Нервов уже ни у кого нет. Скорая не приезжает. Короче, врачи реально вытащили — профессиональная наркологическая клиника на выезде. Поставили систему. В общем, смотрите сами по ссылке — откапаться на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-lnm.ru]https://vyvod-iz-zapoya-na-domu-voronezh-lnm.ru[/url] Не ждите. Перешлите другу.

  2602. Gerardolep

    Reading this slowly in the morning before opening email, and a stop at jemido extended that protected attention, content that earns the prime morning reading slot before the daily distractions begin is content with elevated status and this site has earned that prime slot consistently in my recent reading habits clearly.

  2603. Vivod iz zapoya na domy_meEi

    Народ, попал в такую передрягу. Родственник пьет без остановки. Нервов ни у кого нет. Участковый только руками разводит. Короче, только это и работает — нормальное выведение из запоя капельницей. Приехали. В общем, там и контакты и прайс — вывод из запоя прайс [url=https://vyvod-iz-zapoya-na-domu-voronezh-zqw.ru]вывод из запоя прайс[/url] Промедление смерти подобно. Скиньте кому надо.

  2604. DonovanNeike

    A well calibrated piece that knew its scope and stayed inside it, and a look at sauntersonar maintained the same scope discipline, scope creep is one of the failure modes of long blog posts and this site has clearly invested in the editorial discipline to prevent it which shows up in tightly contained pieces.

  2605. Marcrogma

    Just sat back at the end of the post and felt grateful that someone took the time to write it, and a look at shopflowcenter extended that gratitude across more of the site, recognising effort behind quality work is part of what makes the open web a community rather than just a marketplace today.

  2606. Jamesvieva

    Found something quietly useful here that I expect to return to, and a stop at bomkix added more of the same, content with quiet utility ages well in a way that flashy hot takes do not and I have learned to weight quiet utility much higher when deciding what to bookmark for later use.

  2607. ConnerMen

    Anyone curious about this topic would do well to start here, the foundation laid is solid, and a stop at crystalcovecraftcollective would round out their understanding nicely, this is the kind of resource I would point a friend toward without hesitation if they asked me where to begin learning about anything in this area.

  2608. JermaineBuh

    One of the more thoughtful posts I have read recently on this topic, and a stop at mintorchardcraftcollective added even more weight to that impression, this is genuinely good content that holds its own against far better known sites in the same space without trying to imitate any of them at all which I appreciate.

  2609. Omarwat

    Most of my reading time goes to a small number of trusted sources and this one is now joining that group, and a stop at humcamp reinforced the group membership, the few sites that earn a place in my regular rotation are sites I expect ongoing returns from and this one has earned that elevated position consistently.

  2610. Vivod iz zapoya na domy_yqmt

    Представьте ситуацию, куча народу сталкивается. Каждые выходные одно и то же. В такой теме очень важно не заниматься самодеятельностью. Я нарыл инфу — срочный вывод из запоя. Клиника с лицензией. Если честно, вот собственно источник — вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-kmp.ru]вывод из запоя на дому[/url] Не тяните резину, так как алкоголь — это яд. Настоятельно рекомендую.

  2611. ManuelSails

    Closed the post with a small satisfied sigh, and a stop at solidtruffle produced the same gentle exhale, content that ends well is content that respects the rhythm of reading and the writers here have clearly thought about how their pieces close rather than just trailing off when they run out of things to say.

  2612. CooperSex

    Worth flagging that this approach to the topic is fresh without being contrarian, and a stop at fibdot extended the same fresh angle, finding original perspective on familiar subjects is rare and this site has clearly developed its own way of seeing rather than echoing the dominant takes from elsewhere consistently.

  2613. JesusDer

    On reflection this is the kind of writing that improves my taste for what is possible in the format, and a look at rainharborcraftcollective continued raising that bar, content that elevates my expectations rather than lowering them is doing important work in calibrating my standards and this site is participating in that elevation reliably.

  2614. FelixLoard

    Got something practical out of this that I can apply later this week, and a stop at floraridgemerchantgallery added more details to think about, this is exactly the kind of content I bookmark for future reference rather than the throwaway listicles that dominate most search results these days for almost any common topic.

  2615. LeeJunny

    Felt this in a way I cannot quite explain, the topic just hit different here, and a stop at vaultscript continued in that vein, sometimes you find a site whose perspective lines up with how you have been thinking and reading their work feels like a small relief which I appreciated more than I expected.

  2616. Deonkig

    Picked up two new ideas that I expect will come up in conversations this week, and a look at quickdealscorner added another, content that arms me with talking points rather than just filling time is the kind that provides ongoing value beyond the moment of reading and this site is generating that kind of ongoing value.

  2617. OctavioVag

    Bookmark earned, share earned, return visit earned, all from one reading session, and a look at alpinecovemerchantgallery did the same, the trifecta of bookmark and share and return is rare in a single visit and represents the highest level of engagement I tend to offer any piece of online content these days here.

  2618. HenryFed

    Held my interest from the opening line through to the closing thought, and a stop at oliveorchardcraftcollective did the same, content that earns sustained attention in an environment full of distractions is doing something right and this site is clearly doing several things right rather than just one or two which I really appreciate.

  2619. CooperAcing

    Decided after reading this that I would check this site weekly going forward, and a stop at meadowharbormerchantgallery reinforced that commitment, deciding to add a site to a regular rotation requires meeting a quality bar that very few places clear and this one cleared it cleanly without any noticeable effort or marketing push behind it.

  2620. Tomexcum

    Found a couple of useful angles in here I had not considered before reading carefully, and a quick stop at forestbrooktradingfoundry added more, this is one of those sites where the value compounds the more you read rather than peaking at one viral post and then offering nothing else of substance afterwards which is common.

  2621. LeonWerly

    Found this through a search that was generic enough I did not expect quality results, and a look at tractsmoke continued the surprisingly good experience, search engines occasionally still surface excellent independent content if you scroll past the obvious paid and high authority results which is reassuring to remember sometimes.

  2622. Eugenemyday

    Honestly impressed by the consistency of voice across what I have read so far, and a quick visit to elfincinder continued that consistent feel, when a site reads like one careful person rather than a committee the experience is more rewarding for the reader who notices these subtle editorial details over time.

  2623. Vivod iz zapoya na domy_ffol

    Люди, ситуация жуткая когда — человек уже пятый день под завязку. Соседи звонят в дверь. А скорая не едет. Я через это прошёл. Короче, проверенный способ — адекватный вывод из запоя цены нормальные. Откачали и спать уложили. В общем, сохраняйте себе на будущее — вывод из запоя круглосуточно [url=https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru]https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru[/url] Не надейтесь на авось. Здоровье дороже. Перешлите тому кто в беде.

  2624. Alfredokef

    Worth recognising that the post handled a familiar topic without reaching for any of the obvious hot takes, and a stop at infinitytrendzone continued that fresh treatment, sites that find new angles on subjects others have exhausted are sites worth following carefully and this one has clearly developed that exploratory instinct through patient practice.

  2625. ChaseCip

    Quiet confidence runs through the whole post, no need to shout to make the points stick, and a stop at jencap carried that same restrained voice forward, content that respects the reader by trusting its own substance rather than dressing it up in theatrical language is what I look for online and rarely actually find these days.

  2626. Vivod iz zapoya na domy_sboi

    Блин народ, ситуация просто аховая. Отец не вылезает из бутылки. Думали конец. В платную клинику денег нет. Короче, единственное что реально помогло — качественный вывод из запоя на дому. Через час были. В общем, сохраняйте — вывод из запоя на дому недорого [url=https://vyvod-iz-zapoya-na-domu-voronezh-lnm.ru]вывод из запоя на дому недорого[/url] Промедление смерти подобно. Сохраните себе.

  2627. Ericinpum

    The structure of the post made it easy to follow without losing track of where I was, and a look at sageharbormerchantgallery kept the same logical flow going, this site clearly understands that organisation is half the battle in keeping readers engaged from the first line to the last across any kind of post.

  2628. Vivod iz zapoya na domy_uvEi

    Слушайте, столкнулся с такой ситуацией. Человек просто в штопоре. Думал уже всё. Участковый только руками разводит. Короче, единственное что реально помогло — профессиональный вывод из запоя на дому. Приехали. В общем, смотрите сами по ссылке — вывести из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-zqw.ru]вывести из запоя на дому[/url] Не тяните. Скиньте кому надо.

  2629. Gordonric

    A quiet piece that did not try to compete on volume, and a look at vectorswift maintained that selective approach, sites that publish less but better are increasingly rare in an environment that rewards volume and this one has clearly chosen quality cadence over quantity which is a brave editorial decision in current conditions.

  2630. AngelEmano

    Appreciated how the writer anticipated the questions a reader might have along the way, and a stop at derbunch continued that thoughtful approach, you can tell when content has been edited with the reader in mind versus just published as a first draft and this is clearly the former approach across what I read.

  2631. Trevorquoft

    Well structured and easy to read, that combination is rarer than people think, and a stop at elmharborartisanexchange confirmed the same standard runs across the rest of the site, definitely the kind of place I will be coming back to when this topic comes up in conversation later again over the weeks ahead.

  2632. MaxGam

    Reading this prompted me to dig into a related topic later, and a stop at jeqblot provided some of the starting points for that follow up reading, content that triggers further exploration rather than satisfying curiosity completely is content with real generative energy and this site has plenty of that energy throughout it.

  2633. Eddielurne

    Now thinking the topic is more interesting than I had given it credit for, and a stop at mooncoveartisanexchange continued that elevated interest, content that revives my curiosity about subjects I had set aside is doing genuine work in the structure of my interests and this site is providing that revivifying effect today actually.

  2634. Petercleni

    Pleasant surprise, the post delivered more than the headline promised, and a stop at bayharbormerchantgallery continued that pattern of under promising and over delivering, the rarest combination on the modern web where most content does the opposite by promising the world and delivering thin recycled summaries instead each time you click on something interesting.

  2635. UlyssesDut

    A piece that did not require external context to follow, and a look at humzap maintained the same self contained quality, content that stands alone without forcing readers to chase prerequisites is more accessible and this site has clearly thought about how each piece can serve a fresh visitor rather than only existing members.

  2636. SergioFlout

    Thanks for the breakdown, it gave me a clearer picture of something I had been confused about for a while now, and a stop at jifedge closed the remaining gaps in my understanding nicely, no need to hunt around twenty other articles to put the pieces together which is a real time saver.

  2637. Arthurwen

    Decided to set aside time later to read more carefully, and a stop at violavenom reinforced that decision, content that earns a calendar entry rather than just a passing read is in a different tier altogether and this site is clearly working at that elevated level which I really do appreciate as a reader today.

  2638. Billwap

    Honestly informative, the writer covers the ground without showing off, and a look at fashiondealshub reflected the same humility, content that respects the reader rather than trying to dazzle them is something I always appreciate and rarely come across in this corner of the internet today across the topics I usually read.

  2639. 888starz_qyot

    عزيزتي، يمكنك زيارة [url=https://888star-888starz.com/]888srarz[/url] للاستفادة من عروض ومراهنات حصرية.
    تعمل فرق الدعم في 888starz على مساعدة المستخدمين وحل المشاكل بسرعة.

    القسم الثاني:
    تسعى 888starz للحصول على تراخيص وشهادات تضمن مصداقية عملها في الأسواق المختلفة.

    القسم الثالث:
    يساعد نظام الولاء في 888starz اللاعبين على الحصول على مزايا إضافية وخدمات مخصصة.

    القسم الرابع:
    تعمل المنصة على استكشاف تقنيات حديثة لتقديم تجارب ألعاب متميزة ومبتكرة.

  2640. BarryNab

    Now organising my browser bookmarks to give this site easier access, and a look at flyburn earned the same organisational priority, the small acts of digital housekeeping I do for sites I expect to use often are themselves a measure of trust and this site has triggered the trust based housekeeping behaviour from me clearly.

  2641. Bobcoist

    Even from a single post the editorial care is clear, and a stop at duneelfin extended that care across more pages, the kind of attention to quality that shows up in every paragraph is what separates serious sites from the rest and this one has clearly invested in that paragraph level attention across what I have read.

  2642. Mitchellvax

    Worth recommending broadly to anyone who reads on the topic, and a look at ravensummitcraftcollective only confirms that, the rare combination of accessibility and depth in this site makes it suitable for both newcomers and people who already know the area which is hard to pull off in any blog format today and rarely managed.

  2644. Vivod iz zapoya na domy_utSa

    Друзья ситуация. Жесть просто полная. Брат пьёт без остановки. Жена рыдает. Скорая не едет на такие вызовы. Короче, единственное что реально работает — доступный вывод из запоя цены адекватные. Откачали за час. В общем, там и контакты и прайс — нарколог на дом вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-fds.ru]https://vyvod-iz-zapoya-na-domu-voronezh-fds.ru[/url] Каждый час на счету. Скиньте кому надо.

  2645. Vanceduari

    Took my time with this rather than rushing because the writing rewards attention, and after reliablecartworld I had even more to absorb, the kind of content that pays back the patient reader rather than punishing them with empty filler is something I look for and rarely find in regular searches lately.

  2646. Oscargella

    Thanks for not padding this with the usual filler intros and outros that every other blog seems to require, and a quick visit to tidaltunic continued that lean approach across more posts, content stripped of waste is content that respects you and I will always come back to that kind of approach.

  2647. Vivod iz zapoya na domy_wkKn

    Ребята выручите. Жесть полная случилась. Отец не вылезает из запоя. Соседи уже стучат. Скорая не приезжает на такие вызовы. Короче, единственное что реально помогло — срочный вывод из запоя круглосуточно. Приехали через час. В общем, там контакты и прайс и условия — откапаться на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-ayu.ru]https://vyvod-iz-zapoya-na-domu-voronezh-ayu.ru[/url] Не надейтесь на авось. Перешлите тому кому надо.

  2648. Pedrogause

    Decided not to comment because the post said what needed saying, and a stop at gingercovemerchantgallery continued that complete feel, content that does not invite obvious additions or corrections from readers is content that has been carefully considered and this site appears to consistently produce pieces that satisfy rather than provoke unnecessary follow ups.

  2649. TaylorTag

    Most of my reading time goes to a small number of trusted sources and this one is now joining that group, and a stop at elfindragon reinforced the group membership, the few sites that earn a place in my regular rotation are sites I expect ongoing returns from and this one has earned that elevated position consistently.

  2650. 888starz_aper

    [url=https://888stareg.com/]موقع مراهنات 888[/url]
    يمكن للمستخدمين الجدد في 888starz eg الاستفادة من مكافآت ترحيبية وعروض ترويجية متنوعة.

    القسم الثاني:
    تتميز المنصة بتشكيلة شاملة من الأحداث الرياضية التي يمكن المراهنة عليها مباشرة.

    القسم الثالث:
    تسعى المنصة إلى تحديث مكتبتها من الألعاب بانتظام لتلبية أذواق مختلفة.

    القسم الرابع:
    تهتم 888starz eg بأمان المستخدم وحماية بياناته من خلال تقنيات تشفير متقدمة.

  2651. Coledop

    Reading this in pieces over a coffee break and finding it consistently rewarding, and a stop at mintorchardmerchantgallery extended that into related material I will return to later, the kind of site that fits naturally into small reading windows without requiring a long uninterrupted block is genuinely useful for how I actually browse.

  2652. 888starz_ammr

    زوروا [url=https://888star-egypt.com/]888starz.[/url] للمزيد من المعلومات والعروض الخاصة.
    في عالم الترفيه عبر الإنترنت، يشغل 888starz egypt مكانة بارزة بين المنصات المشهورة.
    تقدم المنصة مجموعة متنوعة من الألعاب والخدمات المصممة لتلبية احتياجات اللاعبين. تقدم المنصة مجموعة متنوعة من الألعاب والخدمات المصممة لتلبية احتياجات اللاعبين.
    تتميز الواجهة بسهولة الاستخدام وسرعة الاستجابة. تتفوق واجهة المستخدم في المنصة بوضوح التصميم وسرعة الأداء.

    القسم الثاني:
    تتضمن عروض 888starz egypt مكافآت ترحيبية للمشتركين الجدد. تتضمن عروض 888starz egypt مكافآت ترحيبية للمشتركين الجدد.
    كما توجد حملات ترويجية مستمرة لزيادة التفاعل مع اللاعبين. وتدير 888starz egypt برامج ترويجية منتظمة لرفع مستوى النشاط داخل الموقع.
    تتنوع الجوائز بين رصيد مجاني ودورات لعب ومزايا خاصة. وتشمل الجوائز أرصدة مجانية وفرص لعب ومزايا إضافية للأعضاء.

    القسم الثالث:
    يعتمد محتوى 888starz egypt على مجموعة من المزودين العالميين للألعاب. تستند ألعاب 888starz egypt إلى محتوى مقدم من شركات ألعاب دولية.
    هذا يضمن تنوعاً وجودة في الخيارات المتاحة للمستخدمين. هذا يضمن تنوعاً وجودة في الخيارات المتاحة للمستخدمين.
    كما تلتزم المنصة بتحديث محتواها بانتظام لمواكبة التطورات. وتعمل 888starz egypt على تحديث مكتبتها باستمرار لمتابعة الجديد.

    القسم الرابع:
    تولي 888starz egypt أهمية لأمان المعاملات وحماية البيانات الشخصية. تولي 888starz egypt أهمية لأمان المعاملات وحماية البيانات الشخصية.
    تستخدم تقنيات تشفير وحلول دفع آمنة لتقليل المخاطر. تستخدم تقنيات تشفير وحلول دفع آمنة لتقليل المخاطر.
    يمكن للمستخدمين التواصل مع دعم فني متوفر لمعالجة أي قضايا بسرعة. ويستطيع الأعضاء الاتصال بخدمة العملاء لحل المشكلات بسرعة وكفاءة.

  2653. Mariowap

    Skipped the related links section thinking I had read enough and then came back to it later when curiosity got the better of me, and a stop at slateserif confirmed I should have just read it first, every section of this site appears to deserve careful attention rather than skipping past lazily.

  2654. Vivod iz zapoya na domy_hwoi

    Всем привет, такая херня приключилась. Отец не вылезает из бутылки. Думали конец. Скорая не приезжает. Короче, единственное что реально помогло — нормальное выведение из запоя капельницей. Отошёл за полчаса. В общем, сохраняйте — вывод из запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-voronezh-lnm.ru]вывод из запоя на дому цена[/url] Не ждите. Сохраните себе.

  2655. Daltonwilky

    Appreciated that the writer trusted the reader to follow along without constant restating of earlier points, and a look at orchardharborartisanexchange continued that respect for the reader, treating an audience as capable adults rather than as people to be hand held through every paragraph is something I notice and value highly across the open internet today.

  2656. Keithdaf

    Reading this confirmed a small detail I had been uncertain about, and a stop at camelcinder provided the source for further checking, content that supports verification through citations or links rather than just asserting facts is more trustworthy and this site has clearly built its credibility through that kind of verifiable approach consistently.

  2657. Vivod iz zapoya na domy_kfol

    Ребята, ситуация жуткая когда — близкий совсем не выходит из штопора. Соседи звонят в дверь. А скорая не едет. Я через это прошёл. Короче, врачи-спасатели настоящие — качественный вывод из запоя на дому. Примчались за час. В общем, сохраняйте себе на будущее — вывод из запоя цена [url=https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru]https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru[/url] Не надейтесь на авось. Здоровье дороже. Перешлите тому кто в беде.

  2658. DarylTut

    Vague feelings of recognition kept surfacing as I read because the writing names things I have been thinking, and a look at moderntrendarena produced more of those recognition moments, content that gives shape to private intuitions is content that makes me feel less alone in my own thinking and this site has that effect.

  2659. Vivod iz zapoya na domy_mlEi

    Ребята, столкнулся с такой ситуацией. Близкий уже неделю не просыхает. Думал уже всё. Скорая не едет. Короче, только это и работает — адекватный вывод из запоя цены приемлемые. Приехали. В общем, там и контакты и прайс — снятие интоксикации на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-zqw.ru]снятие интоксикации на дому[/url] Не надейтесь на авось. Скиньте кому надо.

  2660. CoreyBap

    A piece that read smoothly because the writer understood how readers actually move through prose, and a look at silkgrovemerchantgallery maintained the same reader awareness, writers who think about the reading experience as much as the writing experience produce better work and this site has clearly made that shift in editorial approach.

  2661. IsaiahPew

    Reading this fit naturally into my afternoon walk because I was reading on my phone, and a stop at jeqblue continued well in that walking format, content that survives mobile reading without becoming awkward is content with format flexibility and this site has clearly thought about how it reads across different devices today.

  2662. 888starz_pgEr

    888starz [url=https://amritawalia-art.com/2026/01/14/888starz-%d9%85%d8%b5%d8%b1-%d9%85%d8%b1%d8%a7%d9%87%d9%86%d8%a7%d8%aa-%d8%b1%d9%8a%d8%a7%d8%b6%d9%8a%d8%a9-%d9%85%d8%a8%d8%a7%d8%b4%d8%b1%d8%a9-%d9%88%d9%83%d8%a7%d8%b2%d9%8a%d9%86%d9%88-%d9%85%d8%b9/]888starz[/url].
    يُعد موقع 888starz الرسمي في مصر وجهة متكاملة تجمع بين الرهانات الرياضية وألعاب الكازينو في مكان واحد.

    يدعم القسم المراهنة المباشرة وقت المباراة مع بث للنتائج والإحصائيات الفورية.

    تتوفر تجربة الكازينو المباشر مع موزعين حقيقيين على مدار الساعة.

    من الضروري الاطلاع على أحكام العروض وممارسة اللعب المسؤول لتجنب المخاطر المالية.

  2663. Dillonniz

    Appreciate the practical examples, they made the abstract points easier to grasp, and a stop at tealthicket added more of the same, this site clearly understands that real examples beat empty theory every single time which is the mark of a writer who knows their audience well and respects their time.

  2664. JasonPaich

    Игроки выбирают казино Пинко за прозрачные условия и стабильную работу. Регулярные турниры и еженедельный кэшбэк дают игрокам дополнительную выгоду. Все слоты работают на сертифицированных генераторах случайных чисел, поэтому исходы честные. Фильтры и поиск помогают найти любимую игру за считанные секунды. Мобильная версия полностью адаптирована и работает без задержек на любом устройстве. Начните игру прямо сейчас через Пинко онлайн.

  2665. Oscarinase

    A piece that demonstrated competence without performing it, and a look at derburn maintained the same self assured but unshowy register, the gap between competence and performance of competence is one I track and this site has clearly chosen to demonstrate rather than perform which I find much more persuasive as a reader.

  2666. MylesExibe

    Looking at this from the perspective of someone tired of generic content the contrast is striking, and a look at alpineharborcommercegallery maintained that distinctive feel, sites with strong editorial identity stand out against the bland background of algorithmic content and this one has clearly developed an identity worth recognising through careful attention.

  2667. WendellDot

    I learned more from this short post than from longer articles I read earlier today, and a stop at igoblob added even more useful detail without going off topic, this site clearly knows how to keep things focused without sacrificing depth which is a hard balance to strike for any writer.

  2668. Bradsmavy

    A piece that read smoothly because the writer understood how readers actually move through prose, and a look at canyonharbormerchantgallery maintained the same reader awareness, writers who think about the reading experience as much as the writing experience produce better work and this site has clearly made that shift in editorial approach.

  2670. Lorenzoquomy

    Now planning to recommend this site in a context where my recommendations are taken seriously, and a stop at jesaria confirmed I should make that recommendation soon, the small but real act of recommending content into spaces where my taste matters is something I take seriously and this site is worth the recommendation.

  2671. KobeGoaks

    Reading this slowly in the morning before opening email, and a stop at hupido extended that protected attention, content that earns the prime morning reading slot before the daily distractions begin is content with elevated status and this site has earned that prime slot consistently in my recent reading habits clearly.

  2672. SandyGligo

    Time spent here today felt productive in the way that good reading sessions sometimes do, and a stop at jasperharborcraftcollective extended that productive feeling across the rest of the morning, the difference between productive reading and merely passing time is real and this site is consistently on the productive side for me lately.

  2673. 888starz_ovst

    ????? ?????? ??? ????? ?????? ?? ?????? ??? ???? ??????? ?????????? ???????.
    ???? ????????? ??????? ?????? ??????? ?????? ????? ?????? ?????.
    staz888 [url=https://888starseg.com/]staz888[/url].
    ????? ??????? ??? ??? ???? ????? ?????? ???????? ?? ????? ?????? ????.
    ???? 888starz ????? ????? ?????? ???? ??????? ????? ??????? ??????????.

  2674. DaltonAduff

    Now planning to share the link with a small group of readers I trust, and a look at glybrow suggested more material to share with the same group, recommending content into a curated circle requires confidence in the recommendation and this site is making me confident in those personal recommendations on multiple separate occasions now.

  2675. Portertom

    Found the rhythm of the prose particularly enjoyable on this read through, and a look at rivercoveartisanexchange kept that musical quality going across the related pages, sentence rhythm is something most blog writers ignore but it makes a real difference in how content lands with the careful reader who cares.

  2676. Vivod iz zapoya na domy_cbKn

    Народ привет. Столкнулся с настоящей бедой. Муж просто исчез в бутылке. Жена в истерике. Скорая не приезжает на такие вызовы. Короче, только это и спасло — качественный вывод из запоя на дому. Поставили систему. В общем, жмите чтобы не потерять — срочный вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-ayu.ru]срочный вывод из запоя[/url] Не надейтесь на авось. Скиньте другу в беде.

  2677. Vivod iz zapoya na domy_kmSa

    Народ выручайте. Попал в переплёт конкретный. Отец не выходит из штопора. Жена рыдает. Скорая не едет на такие вызовы. Короче, нормальные врачи попались — качественное выведение из запоя капельницей. Поставили капельницу. В общем, жмите чтобы не потерять — вывод из запоя прайс [url=https://vyvod-iz-zapoya-na-domu-voronezh-fds.ru]https://vyvod-iz-zapoya-na-domu-voronezh-fds.ru[/url] Не надейтесь на авось. Скиньте кому надо.

  2678. PorterMon

    Just enjoyed the experience without needing to think about why, and a look at suppletoast kept that effortless feeling going, sometimes the best content is invisible in the sense that you forget you are reading until you reach the end and realise time has passed without you noticing it pass naturally.

  2679. Grahamtoria

    Reading this with my morning coffee turned into reading the related posts with my morning coffee, and a stop at reliableshoppingzone stretched the morning further, content that pulls breakfast into a reading session rather than just accompanying it is content that has earned a higher claim on my attention than the average article does.

  2680. 888starz_yeor

    تُسهّل الصفحة الرئيسية الوصول إلى جميع الأقسام دون تعقيد أو خطوات إضافية.
    تُظهر الصفحة الرئيسية للموقع الرسمي أهم الأحداث الرياضية وخطوط المراهنة المباشرة.
    لعبه 888 [url=https://888starz-eg-africa.com]https://888starz-eg-africa.com/[/url]
    توفر الصفحة الرئيسية رابطًا مباشرًا لغرف الكازينو المباشر المتاحة على مدار الساعة.
    توفر الصفحة الرئيسية روابط الدعم وطرق الدفع وكل ما يحتاجه اللاعب في مكان واحد.

  2681. Bradleyboari

    Without comparing too aggressively to other sources this one stands out for the right reasons, and a look at unicorntiger continued that distinctive quality, content that distinguishes itself through substance rather than style tricks is content with lasting differentiation and this site has clearly chosen substance based differentiation as its core editorial strategy.

  2682. UlyssesJaf

    Skipped to a specific section because I knew that was the question I had, and the answer was clean, and a stop at elfinebony similarly delivered targeted answers without burying them, content engineered for readers who arrive with specific needs rather than open ended browsing is increasingly valuable in a search heavy reading environment.

  2683. Vivod iz zapoya na domy_laoi

    Народ кто сталкивался, ситуация просто аховая. Муж пьёт неделю без остановки. Думали конец. В бесплатную тащить страшно — поставят на учёт. Короче, врачи реально вытащили — нормальное выведение из запоя капельницей. Поставили систему. В общем, смотрите сами по ссылке — снять запой на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-lnm.ru]https://vyvod-iz-zapoya-na-domu-voronezh-lnm.ru[/url] Промедление смерти подобно. Сохраните себе.

  2684. BennieQuiex

    Excellent post, balanced and well organised without showing off, and a stop at eagleelder continued in that same vein, this site has clearly figured out the formula for content that works for readers rather than for search engine ranking signals which is harder than it sounds today and worth real recognition from anyone.

  2685. 888starz_avmt

    ???? ??????? ???????? ??????? ?????? ??? ??? ????????? ???????? ???? ???????? ???????.
    888 staz [url=https://888starzeg-egypt.com]https://888starzeg-egypt.com/[/url]

  2686. Hughneeni

    If I had encountered this site five years ago I would have been telling everyone about it, and a look at oakcovemerchantgallery extended that retrospective enthusiasm, the version of me who used to recommend favourite blogs frequently would have made sure friends knew about this one and that earlier enthusiasm is partially returning to me here.

  2687. Judesen

    Reading this brought back the satisfaction I used to get from blogs ten years ago, and a stop at savorvantage kept that nostalgic quality alive, sites that capture what was good about an earlier era of internet writing are increasingly precious and this one is doing that without feeling like a deliberate throwback at all.

  2688. 888starz_jlOn

    ???? ?????? ???????? ?????? ?????? 888starz ??????? ?????? ???? ???? ???????? ???????? ?????? ???????? ??????? ?? ???? ????? ???????.
    ???? ?????? ????????? ??????? ???? ?????? ??? ?????? ???????? ??????? ?????? ??? ??????.
    888starz.com [url=https://www.eg888stars.com]https://eg888stars.com/[/url]
    ????? ?????? 888starz ??? ???? ?? 5000 ???? ?? ???? ???????? ??? Pragmatic Play ? NetEnt ? Microgaming.
    ???? ?????? ?????? ????? ???? ??? ??? 50% ???????? ????? ????? ??? ?????????.
    ???? ?????? ???? ?? 30 ???? ????? ?? ?? ????? ???? ???? ?? 5 ??????? ???.
    ???? ????? ????? ??? ???? ?????? ???????? ??????? ??????????? ??? ??????? ??????? ???????.

  2689. JerrySnirl

    A piece that prompted a small mental rearrangement of how I order related ideas, and a look at reliablecartcorner extended that rearranging effect, content that affects the structure of my thinking rather than just adding to it is content with the deepest kind of impact and this site is reaching that depth for me today.

  2690. Caryenric

    Reading this with my morning coffee turned into reading the related posts with my morning coffee, and a stop at vandaltavern stretched the morning further, content that pulls breakfast into a reading session rather than just accompanying it is content that has earned a higher claim on my attention than the average article does.

  2691. Mitchellbow

    A piece that suggested careful editing without showing the marks of the editing, and a look at neoncartcenter continued that invisible polish, the best editing disappears into the prose and this site reads as having been edited with skill that does not announce itself which is the highest compliment I can offer any blog content.

  2692. Kilejacle

    Good quality through and through, no rough edges and no signs of being rushed, and a quick look at skyharbormerchantgallery kept the same polish going, the kind of site that respects its own brand by maintaining consistency across pages which is something I always appreciate as a reader looking for trustworthy information online today.

  2693. Vivod iz zapoya na domy_rgol

    Ребята, сталкивался сам с таким — близкий совсем не выходит из штопора. Дети плачут. А скорая не едет. Я через это прошёл. Короче, единственное что реально вывезло — профессиональное выведение из запоя капельницей. Примчались за час. В общем, смотрите сами по ссылке — снятие запоя цена [url=https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru]https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru[/url] Не тяните резину. Деньги потом не нужны будут. Перешлите тому кто в беде.

  2694. Edmundnig

    Reading this gave me a small sense of progress on a topic I have been slowly working through, and a stop at pearlcoveartisanexchange added another step forward, learning happens in small increments across many sources and finding sources that consistently contribute is the actual practical value of careful curation in an information rich world.

  2695. ShaneTuh

    Useful read, especially because the writer did not assume too much background from the reader, and a quick look at jevmox continued in the same way, a thoughtful site that meets people where they are which is something the modern web could use a lot more of for both casual and serious readers.

  2696. Gilbertohiche

    Top tier post, the kind that makes you want to share the link with friends working in the same area, and a stop at hislex only made me more confident in doing that, this site is one of the better resources I have seen on the topic recently across both new and older posts.

  2697. Donstoni

    Better than most of the writing I have come across on this topic recently, simpler and more direct, and a look at apricotharborcommercegallery continued in that same way, a real outlier in a crowded space full of repetitive content that says little while taking up a lot of reader time today which is unfortunate.

  2698. JordanCom

    Liked that the post resisted a sales pitch ending, and a stop at ileqix maintained the no pitch approach, content that ends without trying to convert me into a customer or subscriber is content that has confidence in its own value and this site is clearly playing the long game on reader trust.

  2699. DevinSed

    Liked the way the post handled the final paragraph, no neat bow but no abrupt cutoff either, and a stop at tennisvortex continued that thoughtful ending pattern, endings are hard and most blog writers either over engineer them or skip them entirely and this site has clearly figured out a sustainable middle approach.

  2700. Vivod iz zapoya na domy_ebKn

    Слушайте сюда. Столкнулся с настоящей бедой. Отец не вылезает из запоя. Дети не спят по ночам. Скорая не приезжает на такие вызовы. Короче, нормальные врачи нашлись — профессиональное выведение из запоя капельницей. Поставили систему. В общем, вся инфа вот здесь — снять запой на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-ayu.ru]https://vyvod-iz-zapoya-na-domu-voronezh-ayu.ru[/url] Не тяните. Перешлите тому кому надо.

  2701. Vivod iz zapoya na domy_jhEi

    Друзья, попал в такую передрягу. Человек просто в штопоре. Руки опускаются. Участковый только руками разводит. Короче, единственное что реально помогло — срочный вывод из запоя круглосуточно. Откачали за час. В общем, там и контакты и прайс — нарколог на дом вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-zqw.ru]нарколог на дом вывод из запоя[/url] Не тяните. Скиньте кому надо.

  2702. DeonTeF

    If I were to recommend a starting point for the topic this site would be near the top of my list, and a stop at coastharborcommercegallery reinforced that recommendation status, the small list of starting point recommendations I keep for friends asking about topics is short and this site is now firmly on it.

  2703. RickyJar

    Reading this gave me a small mental break from the heavier reading I had been doing, and a stop at tracestudio extended that lighter feel, content that provides relief without becoming trivial is harder to produce than people realise and this site has clearly figured out how to be light without being shallow at all.

  2704. BertramHip

    Skipped the social share buttons but might come back to actually use one later, and a stop at elderbeetle extended that share urge, content that triggers genuine sharing impulses rather than performative ones is content that has actually moved me and not many posts in a typical week do that for me actually.

  2705. Vivod iz zapoya na domy_dhSa

    Ребята привет. Столкнулся с такой бедой. Отец не выходит из штопора. Соседи стучат в дверь. В диспансер везти — клеймо на всю жизнь. Короче, единственное что реально работает — качественное выведение из запоя капельницей. Приехали быстро. В общем, сохраняйте себе — вывод из запоя прайс [url=https://vyvod-iz-zapoya-na-domu-voronezh-fds.ru]https://vyvod-iz-zapoya-na-domu-voronezh-fds.ru[/url] Не надейтесь на авось. Скиньте кому надо.

  2706. Kendrickthona

    Reading this prompted me to dig out an old reference book related to the topic, and a stop at rosecoveartisanexchange extended that connection to other sources, content that connects me back to my own existing knowledge rather than asking me to forget it is content with continuity and this site has that continuous quality.

  2707. RonEnunc

    Adding this to my list of go to references for the topic, and a stop at ibeburn confirmed the rest of the site deserves the same, definitely the kind of resource that earns its place rather than getting forgotten the moment the next interesting article shows up in my feed somewhere else on the web.

  2708. JosephLoods

    Reading this in my last reading slot of the day was a good way to end, and a stop at junipercovecraftcollective provided a satisfying close to the reading session, content that ends a day well rather than agitating it before sleep is the kind I value increasingly and this site fits that role for me consistently now.

  2709. Vivod iz zapoya na domy_gtsi

    Народ привет. Попал в жесть полную. Отец не выходит из запоя. Дети не спят ночами. В диспансер везти — на всю жизнь учёт. Короче, нормальные врачи нашлись — качественное выведение из запоя капельницей. Поставили систему. В общем, смотрите сами по ссылке — вывод из запоя цены воронеж [url=https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru]https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru[/url] Не надейтесь на авось. Перешлите тому кому надо.

  2710. AlfredfladO

    Started reading and ended an hour later without realising the time had passed, and a look at shopdeckmarket produced the same time dilation effect, when content makes time feel different the writer has achieved something well beyond the average and this site is producing that experience for me reliably across multiple readings.

  2711. Timlaf

    Reading this in pieces during a long afternoon and finding it consistently rewarding, and a stop at fawndahlia fit naturally into the same fragmented reading pattern, sites whose posts can be read in segments without losing the thread are well suited to how I actually read these days and this one is built well.

  2712. Mauriceacula

    Found this through a search that was generic enough I did not expect quality results, and a look at abobrim continued the surprisingly good experience, search engines occasionally still surface excellent independent content if you scroll past the obvious paid and high authority results which is reassuring to remember sometimes.

  2713. SkylarPed

    Just wanted to drop a quick note saying this was a useful read on a topic I have been circling, no fluff, and a stop at jibtix added a few extra points that fit the same simple style which makes the whole site feel coherent rather than thrown together by many different writers with different goals.

  2714. CristianVat

    Took the time to read every paragraph rather than skimming for the punchline, and a quick visit to aviaryelder earned the same careful attention from me, that is the highest signal I can give about content quality because my default mode is rapid scanning rather than deliberate reading on most pages.

  2715. Juliusmow

    A quiet piece that did not try to compete on volume, and a look at siskatriton maintained that selective approach, sites that publish less but better are increasingly rare in an environment that rewards volume and this one has clearly chosen quality cadence over quantity which is a brave editorial decision in current conditions.

  2716. Jonahamoke

    A piece that did not require external context to follow, and a look at orchardharbormerchantgallery maintained the same self contained quality, content that stands alone without forcing readers to chase prerequisites is more accessible and this site has clearly thought about how each piece can serve a fresh visitor rather than only existing members.

  2717. SterlingTog

    Bookmark folder reorganised slightly to make this site easier to find, and a look at verminturbo earned the same accessibility upgrade, the small organisational moves I make for sites I expect to return to often are themselves a signal of how much I trust them and this site triggered those moves naturally.

  2718. Vivod iz zapoya na domy_ylKn

    Друзья ситуация жуткая. Столкнулся с настоящей бедой. Отец не вылезает из запоя. Жена в истерике. Платные клиники просят бешеные деньги. Короче, только это и спасло — срочный вывод из запоя круглосуточно. Поставили систему. В общем, там контакты и прайс и условия — вывод из запоя цена на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-ayu.ru]вывод из запоя цена на дому[/url] Каждая минута дорога. Перешлите тому кому надо.

  2719. RoderickFak

    Thank you for keeping the writing honest and the points easy to verify against your own experience, and a stop at brightharborcommercegallery reflected the same approach, no exaggeration just steady useful content that I can take with me into my own work without second guessing every sentence I happen to read here.

  2720. Brycemeply

    Following a few of the internal links revealed more posts of similar quality, and a stop at hobcar added more to that growing pile, sites where internal links lead to more good content rather than to more of the same recycled material are sites with depth and this one has clearly built that depth carefully.

  2721. VladimirDeK

    Really appreciate that the writer did not assume I would read every other related post first, and a look at auroraharborcommercegallery kept that self contained feel going where each piece can stand alone, accessibility for new readers is a sign of generous editorial thinking and this site has clearly invested in that approach.

  2722. RubenKes

    My friends would appreciate a few of these posts and I will be sending links accordingly, and a look at topazstrict added more pages to my share queue, content that earns shares to specific people in specific contexts is content with social utility and this site is generating those targeted shares from me consistently lately.

  2723. Vivod iz zapoya na domy_zzoi

    Блин народ, ситуация просто аховая. Отец не вылезает из бутылки. Думали конец. Скорая не приезжает. Короче, только это и спасло — адекватный вывод из запоя цены приемлемые. Через час были. В общем, там контакты и прайс — нарколог на дом вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-lnm.ru]нарколог на дом вывод из запоя на дому[/url] Промедление смерти подобно. Сохраните себе.

  2724. DarrellMor

    Reading this in the time it took to drink half a cup of coffee, and a stop at pebblepinecraftcollective fit naturally into the second half, content that respects the rhythms of a typical morning is content with practical fit and this site has the kind of length and pacing that works for the way I actually read.

  2725. MiguelTix

    Worth saying this site reads better than most paid newsletters I have tried, and a stop at stoneharborcommercegallery confirmed that comparison, the bar for free content is often lower than for paid but this site clears the paid bar consistently and that says something about the editorial approach behind the work being published here regularly.

  2726. Judephemi

    If I had to summarise the editorial sensibility of this site in a few words it would be careful and human, and a look at jifarena extended that summary feeling, capturing the essence of a sites approach in brief is hard but this site has a clear enough identity that the summary comes naturally enough.

  2727. Everettpep

    Took the time to read every paragraph rather than skimming for the punchline, and a quick visit to premiumpickmarket earned the same careful attention from me, that is the highest signal I can give about content quality because my default mode is rapid scanning rather than deliberate reading on most pages.

  2728. Vivod iz zapoya na domy_dyka

    Ребята всем привет. Столкнулся с такой бедой. Человек уже четвёртые сутки в штопоре. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, единственное что реально помогло — качественный вывод из запоя на дому. Приехали через час. В общем, жмите чтобы не потерять — вывод из запоя на дому недорого [url=https://vyvod-iz-zapoya-na-domu-voronezh-plk.ru]вывод из запоя на дому недорого[/url] Не надейтесь на авось. Скиньте другу в беде.

  2729. Vivod iz zapoya na domy_vpSa

    Друзья ситуация. Столкнулся с такой бедой. Брат пьёт без остановки. Жена рыдает. Скорая не едет на такие вызовы. Короче, нормальные врачи попались — лучшая наркологическая клиника с выездом. Поставили капельницу. В общем, смотрите сами по ссылке — снятие запоя цена [url=https://vyvod-iz-zapoya-na-domu-voronezh-fds.ru]https://vyvod-iz-zapoya-na-domu-voronezh-fds.ru[/url] Каждый час на счету. Перешлите другу в беде.

  2730. Vivod iz zapoya na domy_gzsa

    Друзья ситуация. Попал я в переплёт конкретный. Человек уже пятые сутки в штопоре. Соседи стучат в дверь. В диспансер везти — учёт на всю жизнь. Короче, единственное что реально помогло — вывод из запоя дешево и сердито. Приехали через час. В общем, сохраняйте на будущее — выход из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-samara-abc.ru]https://vyvod-iz-zapoya-na-domu-samara-abc.ru[/url] Каждая минута дорога. Перешлите тому кому надо.

  2731. FredTep

    Closed several other tabs to focus on this one as I read, and a stop at daisycovemerchantgallery held my undivided attention the same way, content that earns full focus in an attention environment full of competing pulls is content doing something genuinely well and the team behind it deserves recognition for that achievement consistently.

  2732. Vivod iz zapoya na domy_clOl

    Самарцы всем привет. Попал я в переплёт конкретный. Брат пьёт без остановки. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, единственное что реально помогло — анонимный вывод из запоя без последствий. Отошёл за полчаса. В общем, вся инфа вот здесь — вывод из запоя на дому самара круглосуточно [url=https://vyvod-iz-zapoya-na-domu-samara-def.ru]https://vyvod-iz-zapoya-na-domu-samara-def.ru[/url] Каждая минута дорога. Перешлите тому кому надо.

  2733. Vivod iz zapoya na domy_ddKt

    Самарцы привет. Жесть случилась полная. Близкий не выходит из запоя. Соседи стучат в дверь. Скорая не едет. Короче, нормальные врачи нашлись — профессиональное выведение из запоя капельницей. Отошёл за полчаса. В общем, вся инфа вот здесь — вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-samara-ghi.ru]вывод из запоя на дому[/url] Каждая минута дорога. Скиньте другу в беде.

  2734. JaxonZek

    Reading this in the time it took to drink half a cup of coffee, and a stop at urchinsail fit naturally into the second half, content that respects the rhythms of a typical morning is content with practical fit and this site has the kind of length and pacing that works for the way I actually read.

  2735. Dravenwen

    A clear cut above the usual noise on the subject, and a look at rosecovecraftcollective only made that gap wider in my view, the kind of place that earns its visitors through quality rather than through aggressive marketing or sponsored placements which is increasingly the only way most sites stay afloat across the modern web.

  2736. MattFuh

    A piece that brought a sense of order to a topic I had been finding chaotic, and a look at topaztower continued that organising effect, content that imposes useful structure on messy subjects is doing genuine intellectual work and this site is providing that organisational function across multiple posts I have read recently here.

  2737. KaleLof

    Reading this in a relaxed evening setting was a small pleasure, and a stop at shopaxismarket extended the pleasant evening reading, content that fits the tone of relaxed time without becoming forgettable is what I look for in evening reading and this site has the right tone for that particular slot in my daily reading routine.

  2738. Vivod iz zapoya na domy_hrsi

    Народ привет. Попал в жесть полную. Отец не выходит из запоя. Соседи стучат в дверь. В диспансер везти — на всю жизнь учёт. Короче, единственное что реально помогло — качественное выведение из запоя капельницей. Примчались быстро. В общем, жмите чтобы не потерять — выведение из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru]выведение из запоя[/url] Не тяните. Перешлите тому кому надо.

  2739. Cameronvok

    Considered against the flood of similar content this one stands apart in important ways, and a stop at flintimpala extended that distinctive feel, sites that find their own corner of a crowded topic and stay there are sites worth following and this one has clearly carved out its own space and committed to defending it carefully.

  2740. CassidyNouth

    Reading this slowly in the morning before opening email, and a stop at shopfieldmarket extended that protected attention, content that earns the prime morning reading slot before the daily distractions begin is content with elevated status and this site has earned that prime slot consistently in my recent reading habits clearly.

  2741. Wilburemono

    A piece that did not waste any of its substance on sales or promotion, and a look at sofatavern continued that pure content focus, sites that resist the urge to monetise every paragraph are increasingly rare and this one has clearly made the editorial choice to keep the writing clean from commercial intrusion which I value highly.

  2742. BarryOberb

    A piece that demonstrated competence without performing it, and a look at kettlecrestartisanexchange maintained the same self assured but unshowy register, the gap between competence and performance of competence is one I track and this site has clearly chosen to demonstrate rather than perform which I find much more persuasive as a reader.

  2743. ChrisToisp

    Now planning a longer reading session for the archives, and a stop at jadburst confirmed the archives are worth that longer commitment, sites with archives I want to read deliberately rather than just sample are rare and this one has clearly earned that level of interest based on the consistency of what I have already read.

  2744. Vivod iz zapoya na domy_ylol

    Люди, представляете кошмар — близкий совсем не выходит из штопора. Соседи звонят в дверь. А скорая не едет. Я через это прошёл. Короче, только это и работает — адекватный вывод из запоя цены нормальные. Поставили систему за 20 минут. В общем, смотрите сами по ссылке — вывод из запоя цены воронеж [url=https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru]https://vyvod-iz-zapoya-na-domu-voronezh-jhg.ru[/url] Не надейтесь на авось. Деньги потом не нужны будут. Перешлите тому кто в беде.

  2745. BoydKam

    Reading this confirmed that the topic deserves more careful attention than it usually gets, and a stop at falconcameo extended that elevated framing, content that raises the appropriate weight of a subject without being preachy about it is serving a quiet but important editorial function for the broader cultural conversation about it.

  2746. Vivod iz zapoya na domy_aeKn

    Слушайте сюда. Жесть полная случилась. Близкий человек уже третьи сутки в штопоре. Соседи уже стучат. В диспансер везти — на всю жизнь учёт. Короче, нормальные врачи нашлись — лучшая наркологическая клиника с выездом. Приехали через час. В общем, там контакты и прайс и условия — нарколог на дом вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-ayu.ru]нарколог на дом вывод из запоя на дому[/url] Каждая минута дорога. Перешлите тому кому надо.

  2747. Sylvestertok

    The pacing of the post was just right, never rushed and never dragged out unnecessarily, and a look at atticcondor maintained the same rhythm, you can tell the writer has experience because the difficult skill of pacing is something only practiced writers manage to handle well in long form content over time and across formats.

  2748. PeterEdiny

    Felt the writer was being honest with the reader which is rare enough that I want to acknowledge it, and a look at pebblecreekcommercegallery continued that honest feel, content built on actual knowledge rather than aggregated summaries is something I value highly and rarely come across in regular searches on the open internet these days.

  2749. DwayneTuh

    Appreciated the way each section connected smoothly to the next without abrupt jumps, and a stop at holbook kept that flow going nicely, transitions are something most blog writers ignore but the difference is huge for the reader who is trying to follow a sustained line of thought today across many different topics.

  2750. Rolandoalunk

    A genuine compliment to the writer for keeping the post focused on what mattered, and a look at autumnmeadowcommercegallery continued that disciplined focus, focus is a editorial choice that compounds across many small decisions and this site has clearly made those small decisions consistently across what I have read so far this week here.

  2751. SergioCen

    A piece that was confident enough to leave some questions open rather than forcing closure, and a look at jinblob continued that intellectual honesty, content that admits the limits of its scope is more trustworthy than content that pretends to total understanding and this site has the right calibration on certainty consistently.

  2752. WendellWaics

    Reading this triggered a small reorganisation of my own thinking on the topic, and a stop at scrolltower furthered that reorganisation, content that affects the shape of my mental model rather than just decorating it with new facts is content with structural rather than informational impact and this site provides that.

  2753. Vivod iz zapoya na domy_qesa

    Слушайте что расскажу. Столкнулся с такой бедой. Муж просто пропадает. Соседи стучат в дверь. Скорая не едет. Короче, нормальные врачи нашлись — срочный вывод из запоя круглосуточно. Приехали через час. В общем, сохраняйте на будущее — срочный вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-samara-abc.ru]срочный вывод из запоя[/url] Не надейтесь на авось. Перешлите тому кому надо.

  2754. Vivod iz zapoya na domy_doka

    Слушайте что расскажу. Попал я в переплёт. Близкий не выходит из запоя. Соседи стучат в дверь. Скорая не едет. Короче, единственное что реально помогло — профессиональное выведение из запоя капельницей. Поставили систему. В общем, жмите чтобы не потерять — вывод из запоя недорого [url=https://vyvod-iz-zapoya-na-domu-voronezh-plk.ru]вывод из запоя недорого[/url] Не надейтесь на авось. Скиньте другу в беде.

  2755. Vivod iz zapoya na domy_adSa

    Народ выручайте. Жесть просто полная. Брат пьёт без остановки. Соседи стучат в дверь. Скорая не едет на такие вызовы. Короче, только это и вытащило — доступный вывод из запоя цены адекватные. Приехали быстро. В общем, жмите чтобы не потерять — выведение из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-fds.ru]выведение из запоя[/url] Не тяните. Перешлите другу в беде.

  2756. Darylwon

    A particular pleasure to read this with a fresh coffee, and a look at jinvex extended the pleasure across more pages, content that pairs well with quiet morning rituals is something I have come to value highly and this site has the kind of energy that fits naturally into a calm reading routine.

  2757. Colevek

    Reading this on the train into work was a better use of the commute than my usual choices, and a stop at pineharborcraftcollective extended that commute reading well, content that improves transit time rather than just filling it is content with practical benefit and this site has earned its place in my morning commute reading rotation.

  2758. JesusCor

    A satisfying piece in the way that good meals are satisfying rather than just filling, and a look at scrollturtle extended that satisfaction, the metaphor between content and meals is one I find useful and this site reads as a satisfying meal rather than the empty calories that most content provides for casual readers.

  2759. Philliphax

    Most of the time I bounce off similar pages within seconds, and a stop at borealbarley held me longer than I would have predicted, the ability to convert a likely bouncing visitor into an engaged reader is a quality signal and this site has demonstrated that conversion ability across multiple visits where I expected to bounce.

  2760. CecilZep

    Solid recommendation from me to anyone working in the area, the perspective here is grounded, and a look at premiumpickzone adds even more useful angles, the kind of site that becomes a reference rather than just a one time read which is a higher bar than most blogs ever reach today on the modern web.

  2761. VaughnThuck

    Halfway through I knew I would finish the post, and a stop at rubyorchardartisanexchange also held me through to the end, content that signals its quality early and then sustains it is content with real internal consistency and this site has clearly figured out how to maintain quality from opening sentence through to closing thought.

  2762. Vivod iz zapoya na domy_mnKt

    Слушайте что расскажу. Попал я в переплёт конкретный. Человек уже четвёртые сутки в штопоре. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, только это и спасло — анонимный вывод из запоя без последствий. Приехали через час. В общем, смотрите сами по ссылке — вывод из запоя вызов [url=https://vyvod-iz-zapoya-na-domu-samara-ghi.ru]https://vyvod-iz-zapoya-na-domu-samara-ghi.ru[/url] Каждая минута дорога. Перешлите тому кому надо.

  2763. Gunnerfap

    One of the more thoughtful posts I have read recently on this topic, and a stop at gypsyaspen added even more weight to that impression, this is genuinely good content that holds its own against far better known sites in the same space without trying to imitate any of them at all which I appreciate.

  2764. Vivod iz zapoya na domy_zqsi

    Народ привет. Попал в жесть полную. Брат пьёт без остановки. Соседи стучат в дверь. В диспансер везти — на всю жизнь учёт. Короче, нормальные врачи нашлись — профессиональный вывод из запоя на дому. Поставили систему. В общем, там контакты и прайс и условия — откапаться на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru]https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru[/url] Каждый час на счету. Скиньте другу в беде.

  2765. Vivod iz zapoya na domy_mzKn

    Народ привет. Попал в такую передрягу. Брат пьёт без остановки. Дети не спят по ночам. Платные клиники просят бешеные деньги. Короче, нормальные врачи нашлись — профессиональное выведение из запоя капельницей. Приехали через час. В общем, вся инфа вот здесь — нарколог на дом вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-ayu.ru]нарколог на дом вывод из запоя на дому[/url] Не тяните. Перешлите тому кому надо.

  2766. GeneCaX

    Honest take is that this was better than I expected when I clicked through, and a look at shorevolume reinforced that, the bar for online content has dropped so much that finding something thoughtful and well constructed feels almost noteworthy now which says more about the average than about this site itself.

  2767. MasonFrids

    Now thinking about this site as a small example of what good independent writing looks like, and a stop at dyleko continued that exemplary status, the few sites that serve as good examples are sites worth holding up in conversations about quality and this one has earned that exemplary placement through patient consistent effort over time.

  2768. EliasDremi

    Started forming counter examples to test the claims and the post handled most of them implicitly, and a look at cargofeather continued that anticipatory style, writers who think two steps ahead of the critical reader save themselves from a lot of follow up work and this writer has clearly internalised that habit consistently.

  2769. EanKashy

    A genuine pleasure to find a site that publishes at a sustainable cadence rather than chasing the daily content treadmill, and a look at almondeider confirmed the careful publication rhythm, sites that prioritise quality over frequency are rare and this one has clearly chosen the slower pace which I appreciate as a reader.

  2770. Eduardodeart

    Reading this with a notebook open turned out to be the right move, and a stop at bayougourd added more material to the notes, content that justifies active note taking from a passive reader is content with real informational density and this site is producing notes worthy material at a high rate consistently.

  2771. GregJab

    Highly recommend to anyone looking for a sensible take on this topic without the usual marketing nonsense, and a look at shopplusstore kept that grounded approach going, sites that stay focused on serving readers rather than monetising every click are rare and this is clearly one of those rare ones I really appreciate finding.

  2772. Vivod iz zapoya na domy_liOl

    Слушайте что расскажу. Жесть случилась полная. Близкий не выходит из запоя. Дети не спят ночами. Скорая не едет. Короче, единственное что реально помогло — срочный вывод из запоя круглосуточно. Отошёл за полчаса. В общем, сохраняйте на будущее — вывод из запоя круглосуточно самара [url=https://vyvod-iz-zapoya-na-domu-samara-def.ru]вывод из запоя круглосуточно самара[/url] Каждая минута дорога. Скиньте другу в беде.

  2773. WinstonWaYpe

    Refreshing to read something where the words actually mean something instead of filling space, and a stop at cloverdahlia kept that going, the writing here trusts the reader to follow along without endless repetition or constant reminders of what was already said earlier in the post which I appreciate.

  2774. Dorianuncox

    Felt a small spark of recognition when the post named something I had been struggling to articulate, and a look at jadkix produced more such moments, the rare service of giving readers language for fuzzy intuitions is one of the higher values that good writing can provide and this site offered several today instances.

  2775. BrianWem

    Appreciated the way each section connected smoothly to the next without abrupt jumps, and a stop at kettlecrestcraftcollective kept that flow going nicely, transitions are something most blog writers ignore but the difference is huge for the reader who is trying to follow a sustained line of thought today across many different topics.

  2776. Jakeweers

    Closed and reopened the tab three times before finally finishing, and a stop at caramelcovemerchantgallery held my attention straight through, sometimes content fights for time against my own distraction and the times it wins say something positive about its quality and this post clearly won that fight today afternoon for me.

  2777. Yalehes

    Approaching this with the usual skepticism I bring to new sites and being slowly persuaded, and a stop at vitalsnippet continued that gradual persuasion, the careful path from skeptical reader to genuine fan is the only one I trust and this site has walked me along that path through patient consistent quality across pieces.

  2778. Vivod iz zapoya na domy_gbsa

    Народ выручайте. Жесть случилась полная. Близкий не выходит из запоя. Дети не спят ночами. Скорая не едет. Короче, только это и спасло — анонимный вывод из запоя без последствий. Поставили систему. В общем, смотрите сами по ссылке — капельница от запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-samara-abc.ru]https://vyvod-iz-zapoya-na-domu-samara-abc.ru[/url] Не надейтесь на авось. Скиньте другу в беде.

  2779. Brentmob

    Reading the writers other posts after this one suggests the quality is consistent rather than peak, and a stop at berryharborcommercegallery confirmed the consistent quality reading, sites that hold the same level across many pieces rather than peaking on a few are sites with sustainable editorial discipline and this one has clearly developed that.

  2780. Derrickdaync

    Took longer than expected to finish because I kept stopping to think, and a stop at quickharbormerchantgallery did the same to me, content that provokes thought rather than just delivering information is in a different category and the team here is clearly working at that higher level rather than just cranking out posts.

  2781. ErnestoBoina

    Liked the careful word choice throughout, every term seemed picked for a reason rather than thrown in casually, and a stop at syrupspire continued that precise style, this kind of attention to small details is what separates careful writing from the usual rushed content that dominates blog spaces today across pretty much every topic I follow.

  2782. GaryTub

    Now noticing that the post never raised its voice even when making a strong point, and a look at summitshire continued that calm volume, content that can make important points without resorting to typographic emphasis or emotional appeal is content that trusts its substance to do the work and this site has that confidence consistently.

  2783. Ralphcex

    Started reading expecting to disagree and ended mostly nodding along, and a look at shopeasestore continued the pattern, content that wins agreement through evidence and reasoning rather than rhetorical force is the kind that actually shifts minds and this site clearly knows how to do that across what I have read so far.

  2784. Vivod iz zapoya na domy_qdSa

    Друзья ситуация. Столкнулся с такой бедой. Муж просто исчезает в бутылке. Соседи стучат в дверь. Скорая не едет на такие вызовы. Короче, единственное что реально работает — срочный вывод из запоя круглосуточно. Откачали за час. В общем, жмите чтобы не потерять — выведение из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-fds.ru]выведение из запоя[/url] Каждый час на счету. Перешлите другу в беде.

  2785. Vivod iz zapoya na domy_zqka

    Друзья ситуация. Жесть случилась полная. Человек уже четвёртые сутки в штопоре. Соседи стучат в дверь. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — профессиональное выведение из запоя капельницей. Приехали через час. В общем, смотрите сами по ссылке — вывод из запоя цена на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-plk.ru]https://vyvod-iz-zapoya-na-domu-voronezh-plk.ru[/url] Не надейтесь на авось. Перешлите тому кому надо.

  2786. Brockflord

    Honestly the simplicity is what makes this work, the topic is not buried under filler words or overly complex examples, and a quick look at unicorntempo showed the same sensible style, I left with what I came for and no headache from over reading which is a real win these days.

  2787. Trentbep

    Felt the post had been quietly polished rather than aggressively styled, and a look at syrupserif confirmed the same understated polish, sites whose quality reveals itself slowly rather than announcing itself loudly are the kind I trust more deeply because the trust is not based on first impressions of marketing but actual substance.

  2788. Vivod iz zapoya na domy_awKn

    Друзья ситуация жуткая. Попал в такую передрягу. Муж просто исчез в бутылке. Дети не спят по ночам. Скорая не приезжает на такие вызовы. Короче, нормальные врачи нашлись — адекватный вывод из запоя цены нормальные. Приехали через час. В общем, смотрите сами по ссылке — снятие запоя цена [url=https://vyvod-iz-zapoya-na-domu-voronezh-ayu.ru]снятие запоя цена[/url] Не тяните. Перешлите тому кому надо.

  2789. DalebeX

    Decided to set aside time later to read more carefully, and a stop at silverumber reinforced that decision, content that earns a calendar entry rather than just a passing read is in a different tier altogether and this site is clearly working at that elevated level which I really do appreciate as a reader today.

  2790. BrucePak

    Following a few of the internal links revealed more posts of similar quality, and a stop at banyaneagle added more to that growing pile, sites where internal links lead to more good content rather than to more of the same recycled material are sites with depth and this one has clearly built that depth carefully.

  2791. MiltonShelp

    Skipped past the first paragraph thinking it was setup and had to come back when the rest referenced it, and a stop at rubyorchardcraftcollective similarly rewarded careful reading from the start, content where every paragraph carries weight is content I now know to read from the beginning rather than skipping ahead.

  2792. NedhourL

    Well done, the writing is professional without being stiff, and the topic is treated with care, and a look at primevaluecorner reflected that approach, the kind of site I would point a colleague to if they asked for a reliable starting point on this topic in the future without any hesitation at all.

  2793. Vivod iz zapoya na domy_qdsi

    Слушайте что расскажу. Столкнулся с такой бедой. Отец не выходит из запоя. Жена вся в слезах. Скорая не едет на такие вызовы. Короче, единственное что реально помогло — доступный вывод из запоя цены адекватные. Примчались быстро. В общем, смотрите сами по ссылке — снятие запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru]https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru[/url] Не тяните. Перешлите тому кому надо.

  2794. Omarned

    A thoughtful read in a week that has been mostly noisy, and a look at plumcoveartisanexchange carried that thoughtful quality across more pages, finding pockets of considered writing in a week of distractions is one of the small wins of careful curation and this site is providing those pockets at a sustainable rate.

  2795. AbelPaine

    The overall feel of the post was professional without being stuffy, and a look at siskastencil kept that approachable expertise going, finding the right register for technical content is hard but this site has clearly figured out how to sound knowledgeable without slipping into that distant lecturing tone that loses readers in droves every time.

  2796. Vivod iz zapoya na domy_veKt

    Слушайте что расскажу. Столкнулся с такой бедой. Брат пьёт без остановки. Соседи стучат в дверь. Скорая не едет. Короче, единственное что реально помогло — анонимный вывод из запоя без последствий. Отошёл за полчаса. В общем, там контакты и прайс — вывести из запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-samara-ghi.ru]https://vyvod-iz-zapoya-na-domu-samara-ghi.ru[/url] Не тяните. Скиньте другу в беде.

  2797. Linwoodpaids

    Found this through a search that was generic enough I did not expect quality results, and a look at carobburlap continued the surprisingly good experience, search engines occasionally still surface excellent independent content if you scroll past the obvious paid and high authority results which is reassuring to remember sometimes.

  2798. Eduardodeart

    Now planning to write about the topic myself eventually using this post as a reference, and a look at bayougourd would also serve in that future piece, content that becomes raw material for my own writing rather than just informing my reading is content with multiplicative value and this site is generating that multiplicative effect.

  2799. Gunnergek

    Thank you for keeping the writing honest and the points easy to verify against your own experience, and a stop at ekomug reflected the same approach, no exaggeration just steady useful content that I can take with me into my own work without second guessing every sentence I happen to read here.

  2800. Juliogoona

    Reading this gave me a small sense of progress on a topic I have been slowly working through, and a stop at shopwavemarket added another step forward, learning happens in small increments across many sources and finding sources that consistently contribute is the actual practical value of careful curation in an information rich world.

  2801. FranklinECova

    Quality work here, the post reads cleanly and the points stay focused throughout, and a stop at alpinecobble kept the standard high, you can tell the writer cares about the final result rather than just hitting publish for the sake of having something new on the page to feed the search engines.

  2802. Vivod iz zapoya na domy_bxsa

    Народ выручайте. Столкнулся с такой бедой. Брат пьёт без остановки. Дети не спят ночами. Скорая не едет. Короче, только это и спасло — профессиональное выведение из запоя капельницей. Отошёл за полчаса. В общем, сохраняйте на будущее — прерывание запоев на дому [url=https://vyvod-iz-zapoya-na-domu-samara-abc.ru]https://vyvod-iz-zapoya-na-domu-samara-abc.ru[/url] Не тяните. Перешлите тому кому надо.

  2803. SpencerBow

    Better signal to noise ratio than most places I check on this kind of topic, and a look at tarotshire kept that going, every paragraph here carries something worth reading rather than padding out the page to hit some arbitrary length target that search engines reward but readers ignore as soon as they notice it.

  2804. LesterWeimb

    The examples really helped me grasp the points faster than abstract descriptions would have, and a stop at sambasavor added a few more practical illustrations that drove the message home, the kind of writing that knows its readers learn better through concrete situations rather than vague generalities is rare and worth recognising clearly.

  2805. Kalebwat

    Considered as a whole this site has developed a coherent point of view that comes through in individual pieces, and a look at flintanchor continued displaying that coherence, sites with a unified perspective rather than a grab bag of takes are sites with editorial maturity and this one has clearly developed that maturity through years of work.

  2806. ArnoldoJab

    Working through this site has been a small antidote to the shallow content that fills most of my reading time, and a stop at lanternorchardartisanexchange extended that antidote function, sites that quietly improve the average quality of my reading by being themselves are sites worth supporting through return visits and recommendations consistently.

  2807. JamarcusDem

    Honestly informative, the writer covers the ground without showing off, and a look at jazbox reflected the same humility, content that respects the reader rather than trying to dazzle them is something I always appreciate and rarely come across in this corner of the internet today across the topics I usually read.

  2808. Vivod iz zapoya na domy_ofOl

    Слушайте что расскажу. Жесть случилась полная. Близкий не выходит из запоя. Соседи стучат в дверь. Скорая не едет. Короче, только это и спасло — вывод из запоя дешево и сердито. Отошёл за полчаса. В общем, там контакты и прайс — вывод из запоя на дому самара цены [url=https://vyvod-iz-zapoya-na-domu-samara-def.ru]https://vyvod-iz-zapoya-na-domu-samara-def.ru[/url] Каждая минута дорога. Скиньте другу в беде.

  2809. YaleIniny

    A welcome reminder that thoughtful writing still happens online, and a look at horcall extended that reassurance, the modern web makes it easy to forget that careful writing exists and finding sites that practice it is a small antidote to the cynicism that builds up from too much exposure to algorithmic content.

  2810. CarmineFup

    My time on this site has now extended past what I had budgeted, and a stop at brightharbormerchantgallery keeps extending it further, content that overstays its budget in my schedule is content that has earned the extra time and this site has been earning extra time across multiple visits to the point where my schedule needs adjustment.

  2811. JosephTeddy

    Reading this slowly because the writing rewards a slower pace, and a stop at shoresyrup did the same, the pace at which I read content is something I now use as a quality signal and writing that earns a slower pace earns my attention as a reader looking for substance these days.

  2812. Vivod iz zapoya na domy_cuSa

    Слушайте что расскажу. Попал в переплёт конкретный. Муж просто исчезает в бутылке. Дети не спят ночами. В диспансер везти — клеймо на всю жизнь. Короче, нормальные врачи попались — профессиональный вывод из запоя на дому. Приехали быстро. В общем, там и контакты и прайс — срочный вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-fds.ru]срочный вывод из запоя[/url] Каждый час на счету. Перешлите другу в беде.

  2813. CameronMuh

    Just one of those reads that left me feeling slightly more capable rather than overwhelmed, and a look at quickridgecommercegallery kept that empowering feel going, the difference between content that builds the reader up and content that intimidates them is huge and this site clearly knows which side of that line to stand.

  2814. Vivod iz zapoya na domy_swka

    Народ выручайте. Попал я в переплёт. Муж просто пропадает. Жена в слезах. Платные клиники просят бешеные деньги. Короче, нормальные врачи нашлись — срочный вывод из запоя круглосуточно. Отошёл за полчаса. В общем, вся инфа вот здесь — выведение из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-plk.ru]выведение из запоя[/url] Не тяните. Перешлите тому кому надо.

  2815. Bobbyfaumb

    Most of my reading time goes to a small number of trusted sources and this one is now joining that group, and a stop at stylesteam reinforced the group membership, the few sites that earn a place in my regular rotation are sites I expect ongoing returns from and this one has earned that elevated position consistently.

  2816. EliasSteri

    Now adjusting my mental model of how the topic fits into the broader landscape, and a look at aviarybuckle extended that adjustment, content that affects my structural understanding rather than just my factual knowledge is content with deeper impact and this site is providing those structural updates at a meaningful rate consistently across topics.

  2817. Carlosred

    Appreciated the way each section connected smoothly to the next without abrupt jumps, and a stop at brackenglaze kept that flow going nicely, transitions are something most blog writers ignore but the difference is huge for the reader who is trying to follow a sustained line of thought today across many different topics.

  2818. Andyriz

    Picked a friend mentally as the audience for this and decided to send the link, and a look at seacoveartisanexchange confirmed the send was the right choice, choosing whom to share content with is a small act of curation that I take more seriously than the public sharing most platforms encourage these days online.

  2819. NashCer

    Reading this on the train into work was a better use of the commute than my usual choices, and a stop at ilavex extended that commute reading well, content that improves transit time rather than just filling it is content with practical benefit and this site has earned its place in my morning commute reading rotation.

  2820. Vivod iz zapoya na domy_wvsi

    Ребята выручайте. Столкнулся с такой бедой. Брат пьёт без остановки. Жена вся в слезах. В диспансер везти — на всю жизнь учёт. Короче, нормальные врачи нашлись — профессиональный вывод из запоя на дому. Примчались быстро. В общем, там контакты и прайс и условия — срочный вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru]https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru[/url] Каждый час на счету. Перешлите тому кому надо.

  2821. JadenZoode

    Reading this on a difficult day was a small bright spot, and a stop at sagevogue extended that brightness, content that improves a hard day is content that has earned a particular kind of place in my reading habits and this site is occupying that uplifting role for me today which I appreciate clearly.

  2822. BertramNot

    Solid value for anyone willing to read carefully, and a look at sheentiny extends that value across the rest of the site, this is the kind of place that rewards return visits rather than offering everything in a single splashy post and then leaving readers nothing to come back for later which is unfortunately common.

  2823. Vivod iz zapoya na domy_rfsa

    Народ выручайте. Попал я в переплёт конкретный. Брат пьёт без остановки. Дети не спят ночами. Скорая не едет. Короче, только это и спасло — срочный вывод из запоя круглосуточно. Приехали через час. В общем, жмите чтобы не потерять — вывод из запоя на дому круглосуточно [url=https://vyvod-iz-zapoya-na-domu-samara-abc.ru]https://vyvod-iz-zapoya-na-domu-samara-abc.ru[/url] Не надейтесь на авось. Перешлите тому кому надо.

  2824. Paulbub

    Now setting this aside as a model of how to write thoughtfully on the topic, and a stop at chestnutharbormerchantgallery extended that model status, content that becomes a reference for how a kind of writing should be done is content with influence beyond its own readership and this site is reaching that level for me clearly today.

  2825. EzekielBries

    Honestly enjoyed not being sold anything for the entire duration of the post, and a look at stylishcartzone kept that pleasant absence going across more pages, content that exists for its own sake rather than as a funnel to a paid product is increasingly rare and worth supporting where I can find it.

  2826. QuincyScego

    Probably worth setting aside a longer block to read more carefully than I can right now, and a stop at carobcattail confirmed the longer block plan, the impulse to schedule dedicated time for a sites archive is itself a measure of trust and this site has earned that scheduling impulse from me clearly today actually.

  2827. Vivod iz zapoya na domy_jeKt

    Слушайте что расскажу. Столкнулся с такой бедой. Муж просто пропадает. Соседи стучат в дверь. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — срочный вывод из запоя круглосуточно. Приехали через час. В общем, смотрите сами по ссылке — вывод из запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-samara-ghi.ru]вывод из запоя на дому цена[/url] Не тяните. Скиньте другу в беде.

  2828. Nicholasdam

    High quality writing, no marketing speak and no buzzwords that mean nothing, and a stop at beaconaster kept that going, simple direct content that actually communicates something is harder to find than it should be and this is one of the rare places that gets it right consistently across many different posts.

  2829. JustinFlils

    Found this through a friend who recommended it and now I see why, and a look at aspenfalcon only strengthened that recommendation in my own mind, word of mouth still works for content that actually delivers and this site is clearly earning recommendations the old fashioned way through quality rather than marketing.

  2830. AdamJag

    Looking at this objectively the editorial quality is hard to deny even setting aside personal taste, and a stop at smartonlinemarket maintained the same objective quality, the gap between what I personally enjoy and what is objectively well crafted exists and this site clears both bars simultaneously which is rarer than it sounds.

  2831. Kalebbraro

    My time on this site has now extended past what I had budgeted, and a stop at ambercanyon keeps extending it further, content that overstays its budget in my schedule is content that has earned the extra time and this site has been earning extra time across multiple visits to the point where my schedule needs adjustment.

  2832. Stephencip

    I appreciate the clarity here, everything is explained in simple terms without unnecessary detail, and after a quick stop at ekooat the points came together nicely for me, the writing keeps things straightforward and respects the reader from start to finish without ever talking down to anyone.

  2833. Noelgoamb

    Thank you for not assuming the reader already knows everything, the explanations meet me where I am, and a look at plumcovecraftcollective did the same, that consideration is what makes a site feel welcoming rather than gatekeepy which is sadly the default mood across the modern web today for most subjects covered.

  2834. KaleAngew

    Cuts through the usual marketing fluff that dominates this topic online, and a stop at hupbolt kept the same clean approach going, this is the kind of writing that respects the reader’s time rather than wasting it on repetitive setups before finally getting to the point at hand which is what most sites do.

  2835. Antoniolounc

    Came here from another site and ended up exploring much further than I planned, and a look at calmharborcommercegallery only encouraged more exploration, the kind of place where one click leads to another not through manipulative design but through genuinely interesting content is rare and worth highlighting when found like this somewhere on the open internet.

  2836. EdwinRusty

    Refreshing to find writing that does not try to manipulate the reader into clicking onto the next page through cliffhangers and forced engagement, and a stop at sketchstamp continued in the same respectful way, this is what reader first design actually looks like in practice rather than just in marketing copy that sounds nice.

  2837. Rileyaporb

    Thanks for keeping the writing direct without losing the warmth that makes content feel human, and a stop at lanternorchardcraftcollective carried both qualities forward, balancing professionalism and personality is a rare skill and the writers here have clearly figured out how to consistently land it across many posts which I notice.

  2838. Jaimebrumb

    Worth recognising the specific care that went into how this post ended, and a look at suburbsurge maintained the same careful conclusions, endings are where most blog content falls apart and this site has clearly invested in the closing stretches of its pieces rather than letting them simply trail off when energy fades.

  2839. Vivod iz zapoya na domy_tbSa

    Друзья ситуация. Столкнулся с такой бедой. Брат пьёт без остановки. Дети не спят ночами. Платные клиники ломят космос. Короче, нормальные врачи попались — срочный вывод из запоя круглосуточно. Приехали быстро. В общем, там и контакты и прайс — выведение из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-fds.ru]выведение из запоя на дому[/url] Каждый час на счету. Скиньте кому надо.

  2840. Vivod iz zapoya na domy_lqka

    Слушайте что расскажу. Жесть случилась полная. Муж просто пропадает. Жена в слезах. В диспансер везти — учёт на всю жизнь. Короче, нормальные врачи нашлись — лучшая наркологическая клиника с выездом. Поставили систему. В общем, смотрите сами по ссылке — выведение из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-plk.ru]выведение из запоя на дому[/url] Не тяните. Перешлите тому кому надо.

  2841. Juandrimi

    A handful of memorable phrases from this one I will probably use later, and a look at bagelcameo added a couple more, content that contributes language to my own communication rather than just facts is content with a different kind of utility and this site is providing that linguistic utility consistently across what I read.

  2842. KennethMer

    Reading this slowly to absorb the structure, and the structure is doing real work alongside the words, and a look at roseharborcommercegallery maintained the same architectural quality, when sentence shapes and paragraph rhythms reinforce the meaning rather than just transporting words you know you are reading skilled work today.

  2843. Vivod iz zapoya na domy_hsOl

    Народ выручайте. Столкнулся с такой бедой. Муж просто пропадает. Соседи стучат в дверь. Скорая не едет. Короче, нормальные врачи нашлись — вывод из запоя дешево и сердито. Поставили систему. В общем, там контакты и прайс — анонимный вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-samara-def.ru]анонимный вывод из запоя[/url] Каждая минута дорога. Перешлите тому кому надо.

  2844. Vivod iz zapoya na domy_insa

    Самарцы привет. Столкнулся с такой бедой. Близкий не выходит из запоя. Жена в слезах. В диспансер везти — учёт на всю жизнь. Короче, нормальные врачи нашлись — профессиональное выведение из запоя капельницей. Приехали через час. В общем, смотрите сами по ссылке — прерывание запоя на дому [url=https://vyvod-iz-zapoya-na-domu-samara-abc.ru]https://vyvod-iz-zapoya-na-domu-samara-abc.ru[/url] Не тяните. Скиньте другу в беде.

  2845. Yaledaush

    Glad I stumbled across this post, the explanations actually make sense without needing background knowledge to follow along, and after a stop at azuqix the same was true there, no assumptions about the reader just clear writing that anyone can understand from the first line right through to the end.

  2846. RodneyDiada

    Skipped the related products section because there was none, and a stop at cameoaspen also lacked any aggressive monetisation, content that is not constantly trying to convert me into a customer or subscriber is content that has confidence in its own value and that confidence shows up as a different reading experience.

  2847. Vivod iz zapoya na domy_tgsi

    Ребята выручайте. Столкнулся с такой бедой. Муж просто убивает себя. Жена вся в слезах. Платные клиники ломят бешеные деньги. Короче, единственное что реально помогло — лучшая наркологическая клиника с выездом. Откачали за час. В общем, там контакты и прайс и условия — выведение из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru]выведение из запоя[/url] Не надейтесь на авось. Скиньте другу в беде.

  2848. Logantycle

    A quiet kind of confidence runs through the writing, and a look at sonarsandal carried that same understated assurance, confidence without bragging is the most attractive register for online writing and the writers here have clearly developed it through practice rather than affecting it through stylistic tricks that would feel hollow eventually.

  2849. BobErors

    A handful of memorable phrases from this one I will probably use later, and a look at silkgrovecraftcollective added a couple more, content that contributes language to my own communication rather than just facts is content with a different kind of utility and this site is providing that linguistic utility consistently across what I read.

  2850. Bryanmaf

    High quality writing, no marketing speak and no buzzwords that mean nothing, and a stop at stereoskein kept that going, simple direct content that actually communicates something is harder to find than it should be and this is one of the rare places that gets it right consistently across many different posts.

  2851. JosiahTit

    Honest reaction is that this is the kind of writing I would defend in a conversation about good blog content, and a look at stylishgoodscorner reinforced that, the rare site whose work I would actively recommend rather than just tolerate is the kind I want to support through return visits regularly.

  2852. RichardLax

    Reading this prompted a small redirection in something I was working on, and a stop at tyrantvolume extended that redirecting influence, content that affects my actual work rather than just my thinking has the highest practical impact and this site is providing that level of influence for me at a sustainable rate apparently.

  2853. ForrestNak

    Closed the tab with a small sense of finality rather than the usual rushed exit, and a stop at calicocameo produced the same considered closing, when reading ends with deliberate satisfaction rather than impatient skip you know the time was well spent and this site is producing those satisfying endings consistently across what I read.

  2854. Tyronelerce

    Thank you for not assuming the reader already knows everything, the explanations meet me where I am, and a look at beaconbevel did the same, that consideration is what makes a site feel welcoming rather than gatekeepy which is sadly the default mood across the modern web today for most subjects covered.

  2855. Kareemjar

    Now adding this to a list of sites I want to see flourish, and a stop at cavernfjord reinforced that wish, the few sites I actively root for are sites that produce the kind of work I want more of in the world and this one has joined that small list based on what I have read so far.

  2856. NicolasSetty

    Better than most of the writing I have come across on this topic recently, simpler and more direct, and a look at ambergrouse continued in that same way, a real outlier in a crowded space full of repetitive content that says little while taking up a lot of reader time today which is unfortunate.

  2857. Vivod iz zapoya na domy_huKt

    Самарцы привет. Попал я в переплёт конкретный. Близкий не выходит из запоя. Жена в слезах. Платные клиники просят бешеные деньги. Короче, нормальные врачи нашлись — вывести из запоя на дому качественно. Приехали через час. В общем, там контакты и прайс — вывод из запоя на дому самара [url=https://vyvod-iz-zapoya-na-domu-samara-ghi.ru]вывод из запоя на дому самара[/url] Не тяните. Перешлите тому кому надо.

  2858. Arnoldmow

    Really grateful for content like this, it does not waste my time and it does not insult my intelligence either, and a quick look at eloido was the same, balanced respectful writing that makes a person feel welcome rather than rushed through pages of forced engagement just to keep clicking around.

  2859. Issacarrap

    Reading this confirmed that the topic deserves more careful attention than it usually gets, and a stop at jikbond extended that elevated framing, content that raises the appropriate weight of a subject without being preachy about it is serving a quiet but important editorial function for the broader cultural conversation about it.

  2860. Juddfouro

    Following a few of the internal links revealed more posts of similar quality, and a stop at chestnutharborcommercegallery added more to that growing pile, sites where internal links lead to more good content rather than to more of the same recycled material are sites with depth and this one has clearly built that depth carefully.

  2861. Clydegraiz

    Honestly this kind of writing is why I still bother to read independent sites, and a look at hurbug extended that broader reflection, the few sites that justify continued attention to non algorithmic content are sites like this one and finding them periodically is enough to keep my reading habits oriented toward independent rather than aggregated content.

  2862. JulianMar

    Glad I clicked through from where I did because this turned out to be worth the time spent, and after ravensummitartisanexchange I had a fuller picture, the kind of content that earns its visitors through delivering value rather than chasing them through aggressive advertising or constant pop ups appearing everywhere on the screen lately.

  2863. EdwinAbito

    Felt the post had been quietly polished rather than aggressively styled, and a look at selectshare confirmed the same understated polish, sites whose quality reveals itself slowly rather than announcing itself loudly are the kind I trust more deeply because the trust is not based on first impressions of marketing but actual substance.

  2864. Darnellmepay

    Now feeling that this site is the kind I want to make sure does not disappear, and a look at lavenderharborartisanexchange reinforced that quiet protective feeling, the rare sites whose disappearance would actually matter to me are the sites I want to support through return visits and recommendations and this one has joined that small protected list.

  2865. Vivod iz zapoya na domy_alka

    Слушайте что расскажу. Столкнулся с такой бедой. Человек уже четвёртые сутки в штопоре. Жена в слезах. В диспансер везти — учёт на всю жизнь. Короче, единственное что реально помогло — адекватный вывод из запоя цены нормальные. Приехали через час. В общем, там контакты и прайс — снять запой на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-plk.ru]https://vyvod-iz-zapoya-na-domu-voronezh-plk.ru[/url] Не надейтесь на авось. Скиньте другу в беде.

  2866. CooperBoisk

    Probably going to mention this site in a write up I am working on later this month, and a stop at tokenudon provided more material for that potential mention, content worth referencing in my own published work rather than just personal reading is content with the highest endorsement level and this site has earned that endorsement.

  2867. Vivod iz zapoya na domy_rmsa

    Самарцы привет. Жесть случилась полная. Близкий не выходит из запоя. Жена в слезах. Скорая не едет. Короче, нормальные врачи нашлись — срочный вывод из запоя круглосуточно. Приехали через час. В общем, там контакты и прайс — вывод из запоя на дому в самаре [url=https://vyvod-iz-zapoya-na-domu-samara-abc.ru]https://vyvod-iz-zapoya-na-domu-samara-abc.ru[/url] Не надейтесь на авось. Скиньте другу в беде.

  2868. Vivod iz zapoya na domy_tuMn

    Народ выручайте. Жесть случилась полная. Муж просто пропадает. Жена в слезах. В диспансер везти — учёт на всю жизнь. Короче, единственное что реально помогло — профессиональное выведение из запоя капельницей. Отошёл за полчаса. В общем, вся инфа вот здесь — вывод из запоя частный врач [url=https://vyvod-iz-zapoya-na-domu-samara-mno.ru]https://vyvod-iz-zapoya-na-domu-samara-mno.ru[/url] Каждая минута дорога. Перешлите тому кому надо.

  2869. NoelInfer

    Glad I clicked through from where I did because this turned out to be worth the time spent, and after mintmeadowcommercegallery I had a fuller picture, the kind of content that earns its visitors through delivering value rather than chasing them through aggressive advertising or constant pop ups appearing everywhere on the screen lately.

  2870. Keaganninue

    Reading this prompted a brief but useful conversation with a colleague who happened to walk by, and a stop at silvercovemerchantgallery extended that conversational seed, content that becomes a starting point for in person discussion rather than ending in solitary reading is content with social generative energy and this site has plenty of it apparently.

  2871. Lawsonoxype

    Now planning to write about the topic myself eventually using this post as a reference, and a look at coppercovemerchantgallery would also serve in that future piece, content that becomes raw material for my own writing rather than just informing my reading is content with multiplicative value and this site is generating that multiplicative effect.

  2872. Vivod iz zapoya na domy_ilKt

    Друзья ситуация жуткая. Попал я в переплёт конкретный. Близкий не выходит из запоя. Соседи стучат в дверь. Скорая не едет. Короче, нормальные врачи нашлись — срочный вывод из запоя круглосуточно. Отошёл за полчаса. В общем, там контакты и прайс — вывод из запоя цены [url=https://vyvod-iz-zapoya-na-domu-samara-jkl.ru]вывод из запоя цены[/url] Не надейтесь на авось. Перешлите тому кому надо.

  2873. Vivod iz zapoya na domy_ruSa

    Друзья ситуация. Жесть просто полная. Близкий человек уже шестой день в завязке. Соседи стучат в дверь. Скорая не едет на такие вызовы. Короче, нормальные врачи попались — лучшая наркологическая клиника с выездом. Откачали за час. В общем, жмите чтобы не потерять — вывод из запоя на дому круглосуточно [url=https://vyvod-iz-zapoya-na-domu-voronezh-fds.ru]https://vyvod-iz-zapoya-na-domu-voronezh-fds.ru[/url] Каждый час на счету. Скиньте кому надо.

  2874. Randallalcok

    Really appreciate this kind of writing, no shouting and no clickbait headlines just steady useful content, and a quick look at cobbleiguana kept that going, definitely a site I will be returning to whenever I need a sensible take on similar topics in the days ahead and also during slower work weeks.

  2875. Anthonybef

    Reading this confirmed that the topic deserves more careful attention than it usually gets, and a stop at bisonbatik extended that elevated framing, content that raises the appropriate weight of a subject without being preachy about it is serving a quiet but important editorial function for the broader cultural conversation about it.

  2876. Vivod iz zapoya na domy_vasi

    Народ привет. Попал в жесть полную. Человек уже пятый день в штопоре. Соседи стучат в дверь. В диспансер везти — на всю жизнь учёт. Короче, только это и вытащило — срочный вывод из запоя круглосуточно. Откачали за час. В общем, жмите чтобы не потерять — вывод из запоя с выездом [url=https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru]https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru[/url] Не тяните. Перешлите тому кому надо.

  2877. Willisbioky

    This stands out compared to similar posts I have read recently, less noise and more substance, and a look at turbinevault kept that gap going, you can really feel the difference between content made by someone who cares versus content made to fill a publishing schedule for an algorithm trying to keep growing somehow.

  2878. FrancisFraus

    Took longer than expected to finish because I kept stopping to think, and a stop at camelchamois did the same to me, content that provokes thought rather than just delivering information is in a different category and the team here is clearly working at that higher level rather than just cranking out posts.

  2879. Vivod iz zapoya na domy_urOl

    Народ выручайте. Попал я в переплёт конкретный. Брат пьёт без остановки. Дети не спят ночами. Скорая не едет. Короче, только это и спасло — срочный вывод из запоя круглосуточно. Отошёл за полчаса. В общем, вся инфа вот здесь — вывести из запоя срочно [url=https://vyvod-iz-zapoya-na-domu-samara-def.ru]https://vyvod-iz-zapoya-na-domu-samara-def.ru[/url] Каждая минута дорога. Перешлите тому кому надо.

  2880. Brockjaw

    Great work on keeping things readable, the post never drags or repeats itself which I really appreciate, and a stop at shiretrellis added a bit more context that fit naturally with what was already said here, no need to read everything twice to get the point being made today.

  2881. LedgerEvike

    The conclusions felt earned rather than tacked on at the end like an afterthought, and a look at urbancartzone kept that careful structure going, you can tell when a writer has thought about the shape of their post versus just letting it ramble out and hoping for the best at the end which most do.

  2882. AnthonyKic

    More original than the recycled takes I keep finding on the topic elsewhere, and a quick look at bevelhamlet confirmed it, the kind of site that has its own voice rather than echoing whatever is trending which makes it stand out as a refreshing change from the usual rotation of generic content I see daily.

  2883. Vivod iz zapoya na domy_urKn

    Слушайте сюда. Столкнулся с настоящей бедой. Брат пьёт без остановки. Соседи уже стучат. В диспансер везти — на всю жизнь учёт. Короче, только это и спасло — срочный вывод из запоя круглосуточно. Приехали через час. В общем, смотрите сами по ссылке — вывести из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-ayu.ru]вывести из запоя на дому[/url] Не тяните. Скиньте другу в беде.

  2884. Dalesal

    Probably the kind of site that should be more widely read than it appears to be, and a look at beaconcopper reinforced that quiet wish, the gap between a sites quality and its apparent reach is sometimes large and that gap exists for this site in a way that makes me want to mention it more.

  2885. Lowellbar

    Felt like the post had been edited rather than just drafted and published, and a stop at celerycivet suggested the same care across the site, the difference between edited and unedited content is enormous for the reader and this site has clearly invested in the editing pass that most blogs skip entirely which really does show up.

  2886. MauriceVed

    Reading this slowly to absorb the structure, and the structure is doing real work alongside the words, and a look at antlerebony maintained the same architectural quality, when sentence shapes and paragraph rhythms reinforce the meaning rather than just transporting words you know you are reading skilled work today.

  2887. Darrenmayor

    Came in skeptical and left mostly convinced, that is the highest praise I can offer, and a look at sobertrifle pushed me further in the same direction, content that survives a critical first read is rare and worth recognising because most blog posts crumble under any real scrutiny these days when you actually pay attention closely.

  2888. TomMum

    Decided not to comment because the post said what needed saying, and a stop at elonox continued that complete feel, content that does not invite obvious additions or corrections from readers is content that has been carefully considered and this site appears to consistently produce pieces that satisfy rather than provoke unnecessary follow ups.

  2889. Vivod iz zapoya na domy_iaKt

    Друзья ситуация. Столкнулся с такой бедой. Брат пьёт без остановки. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, единственное что реально помогло — анонимный вывод из запоя без последствий. Отошёл за полчаса. В общем, там контакты и прайс — вывод из запоя цены [url=https://vyvod-iz-zapoya-na-domu-samara-ghi.ru]вывод из запоя цены[/url] Не надейтесь на авось. Скиньте другу в беде.

  2890. JimmyMedge

    Came away with a small but real shift in perspective on the topic, and a stop at sonartennis pushed that shift a bit further, the kind of subtle reframing that good writing does to a reader without making a big deal of it is something I always appreciate when it happens which is sadly not that often.

  2891. Vivod iz zapoya na domy_pasa

    Друзья ситуация. Жесть случилась полная. Человек уже пятые сутки в штопоре. Соседи стучат в дверь. Скорая не едет. Короче, единственное что реально помогло — вывод из запоя дешево и сердито. Приехали через час. В общем, смотрите сами по ссылке — запой вызов на дом [url=https://vyvod-iz-zapoya-na-domu-samara-abc.ru]https://vyvod-iz-zapoya-na-domu-samara-abc.ru[/url] Не надейтесь на авось. Скиньте другу в беде.

  2892. GeraldWex

    Reading the writers other posts after this one suggests the quality is consistent rather than peak, and a stop at ibabowl confirmed the consistent quality reading, sites that hold the same level across many pieces rather than peaking on a few are sites with sustainable editorial discipline and this one has clearly developed that.

  2893. DerrickCof

    Found this through a search that was generic enough I did not expect quality results, and a look at lavenderharborcraftcollective continued the surprisingly good experience, search engines occasionally still surface excellent independent content if you scroll past the obvious paid and high authority results which is reassuring to remember sometimes.

  2894. Vivod iz zapoya na domy_qvMn

    Самарцы привет. Жесть случилась полная. Муж просто пропадает. Жена в слезах. Скорая не едет. Короче, только это и спасло — срочный вывод из запоя круглосуточно. Приехали через час. В общем, вся инфа вот здесь — цена вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-samara-mno.ru]https://vyvod-iz-zapoya-na-domu-samara-mno.ru[/url] Каждая минута дорога. Перешлите тому кому надо.

  2895. Maxwelljoync

    Liked the way the post handled the final paragraph, no neat bow but no abrupt cutoff either, and a stop at sageharborartisanexchange continued that thoughtful ending pattern, endings are hard and most blog writers either over engineer them or skip them entirely and this site has clearly figured out a sustainable middle approach.

  2896. Lelandsen

    Worth flagging this site to a few specific friends who would appreciate the editorial sensibility, and a look at tacticstaff added more pages I will mention to them, recommending sites to specific people requires understanding both the site and the person and this site is making those personalised recommendations easy and natural for me.

  2897. Chandlermaf

    Now adjusting my expectations upward for the topic based on this post, and a stop at jilbrew continued that bar raising effect, content that resets what I think is possible on a subject is doing real work in shaping my standards and this site is providing those bar raising experiences at a notable rate during sessions.

  2898. Vivod iz zapoya na domy_vcOl

    Самарцы всем привет. Попал я в переплёт конкретный. Человек уже седьмые сутки в штопоре. Соседи стучат в дверь. В диспансер везти — учёт на всю жизнь. Короче, только это и спасло — вывод из запоя дешево и сердито. Отошёл за полчаса. В общем, там контакты и прайс — вывод из запоя недорого [url=https://vyvod-iz-zapoya-na-domu-samara-pqr.ru]вывод из запоя недорого[/url] Не тяните. Скиньте другу в беде.

  2899. EarlAcelp

    Now understanding why someone recommended this site to me a while back, and a stop at sunharborcommercegallery explained the recommendation, sometimes recommendations make sense only after experience and this site has finally clicked into place as the kind of resource I now understand was being recommended for sound editorial reasons by my friend.

  2900. Pyblichnaya kadastrovaya karta_eoKl

    Люди подскажите Вечно то данные устаревшие Кадастровые номера и границы Короче, единственный нормальный сервис — публичная кадастровая карта новая с 3D-видом Скачал выписку сразу В общем, вся инфа вот здесь — публичной кадастровой карте (пкк) [url=https://publichnaya-kadastrovaya-karta-abc.ru]https://publichnaya-kadastrovaya-karta-abc.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  2901. AlfonsoLar

    Thanks for putting in the work to make this approachable, plenty of sites cover the same ground but most do it badly, and a quick visit to crocusazalea confirmed this one stands apart, simple language and useful examples without anyone trying to sell me anything along the way which I really appreciated.

  2902. Pyblichnaya kadastrovaya karta_grmr

    Люди помогите То карта тормозит Категорию земли уточнить Короче, нашел крутой инструмент — публичная кадастровая карта новая с просмотром Проверил обременения В общем, смотрите сами по ссылке — кадастровая карта рф официальный сайт [url=https://publichnaya-kadastrovaya-karta-ghi.ru]https://publichnaya-kadastrovaya-karta-ghi.ru[/url] Не парьтесь с росреестром Перешлите тому кто ищет участок

  2903. JudsonnuM

    Honestly impressed, did not expect to find this level of care on the topic, and a stop at garnetcarbon cemented the impression, you can tell within the first few paragraphs whether a site is going to be worth the time and this one delivered on that early promise nicely throughout the rest of what I read.

  2904. Diegocix

    Bookmark added with a small note about why, and a look at flintcivet prompted another bookmark with another note, the bookmarks I annotate are the ones I expect to return to deliberately rather than stumble into and this site is generating annotated bookmarks at a higher rate than my usual content sources by some margin.

  2905. Jonahprots

    Now adding this site to a small mental group of recommendations I keep ready for specific kinds of inquiries, and a stop at eskimocarob extended the recommendation readiness, content that I can confidently point friends and colleagues toward in specific contexts is content with real social utility and this site has that utility clearly.

  2906. Vivod iz zapoya na domy_gysi

    Ребята выручайте. Столкнулся с такой бедой. Отец не выходит из запоя. Дети не спят ночами. В диспансер везти — на всю жизнь учёт. Короче, единственное что реально помогло — срочный вывод из запоя круглосуточно. Поставили систему. В общем, вся информация вот здесь — стоимость вывода из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru]https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru[/url] Каждый час на счету. Скиньте другу в беде.

  2907. Garrettvok

    During a reading session that included several other sources this one stood out, and a look at vocabtoffee continued the standout quality, the side by side comparison of sources during research is a useful exercise and this site has been winning those comparisons for me consistently across multiple research sessions during the last week.

  2908. Vivod iz zapoya na domy_xaKt

    Народ выручайте. Столкнулся с такой бедой. Муж просто пропадает. Дети не спят ночами. Скорая не едет. Короче, нормальные врачи нашлись — профессиональное выведение из запоя капельницей. Отошёл за полчаса. В общем, там контакты и прайс — снятие запоев на дому [url=https://vyvod-iz-zapoya-na-domu-samara-jkl.ru]https://vyvod-iz-zapoya-na-domu-samara-jkl.ru[/url] Каждая минута дорога. Перешлите тому кому надо.

  2909. Zanehog

    Closed the tab with a small sense of finality rather than the usual rushed exit, and a stop at carobhopper produced the same considered closing, when reading ends with deliberate satisfaction rather than impatient skip you know the time was well spent and this site is producing those satisfying endings consistently across what I read.

  2910. Rickblist

    Worth saying that the prose reads naturally without straining for style, and a stop at solacetomato maintained the same unforced quality, writing that achieves elegance without effort is the highest tier and this site has clearly worked out how to land that effortless quality consistently rather than only on the writers best days.

  2911. Bryceges

    Reading this in a relaxed evening setting was a small pleasure, and a stop at urbanflashhub extended the pleasant evening reading, content that fits the tone of relaxed time without becoming forgettable is what I look for in evening reading and this site has the right tone for that particular slot in my daily reading routine.

  2912. Vivod iz zapoya na domy_xjKn

    Ребята выручите. Столкнулся с настоящей бедой. Близкий человек уже третьи сутки в штопоре. Дети не спят по ночам. В диспансер везти — на всю жизнь учёт. Короче, только это и спасло — лучшая наркологическая клиника с выездом. Приехали через час. В общем, сохраняйте на будущее — выведение из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-ayu.ru]выведение из запоя на дому[/url] Не надейтесь на авось. Перешлите тому кому надо.

  2913. LeonInput

    Worth marking this site as one to come back to deliberately rather than by accident, and a stop at heronfjord reinforced that intention, the difference between sites I find again by chance and sites I return to on purpose is meaningful and this one has clearly moved into the deliberate return category for me.

  2914. DonLax

    Now realising the post solved a small problem I had been carrying for weeks, and a look at cobradamson extended that problem solving function, content that connects to specific unresolved questions in my own life rather than just providing general interest is content with real practical impact and this site is providing that practical value.

  2915. FletcherDrime

    Really appreciate the lack of pop ups, modals, cookie banners stacking on top of each other, and a quick visit to apronbadge confirmed the same clean approach across the rest of the site, technical decisions about user experience are part of what makes content actually pleasant to engage with for sure.

  2916. EnzoFib

    Felt like I was reading something written by someone who actually thinks about the topic rather than reciting it, and a look at velvetgrovecommercegallery reinforced that impression, the difference between recited content and considered content is huge and this site clearly belongs to the latter category which I appreciate as a careful reader looking for substance.

  2917. SterlingTherb

    Honestly this was a good read, no jargon and no padding, and a short look at cloverhedge kept that same feel going which I really appreciated, the writer clearly knows the topic well enough to explain it without hiding behind big words or filler that often gets used to seem clever.

  2918. Vivod iz zapoya na domy_fkOl

    Народ выручайте. Жесть случилась полная. Брат пьёт без остановки. Соседи стучат в дверь. Платные клиники просят бешеные деньги. Короче, нормальные врачи нашлись — вывод из запоя дешево и сердито. Приехали через час. В общем, смотрите сами по ссылке — вывод из запоя на дому недорого [url=https://vyvod-iz-zapoya-na-domu-samara-def.ru]вывод из запоя на дому недорого[/url] Не надейтесь на авось. Скиньте другу в беде.

  2919. Vivod iz zapoya na domy_maMn

    Народ выручайте. Попал я в переплёт конкретный. Близкий не выходит из запоя. Соседи стучат в дверь. Скорая не едет. Короче, нормальные врачи нашлись — вывод из запоя дешево и сердито. Поставили систему. В общем, сохраняйте на будущее — вывод из запоя цены самара [url=https://vyvod-iz-zapoya-na-domu-samara-mno.ru]https://vyvod-iz-zapoya-na-domu-samara-mno.ru[/url] Не тяните. Скиньте другу в беде.

  2920. RayElded

    Skipped to a specific section because I knew that was the question I had, and the answer was clean, and a stop at beavercactus similarly delivered targeted answers without burying them, content engineered for readers who arrive with specific needs rather than open ended browsing is increasingly valuable in a search heavy reading environment.

  2921. Noelgal

    Came in confused about the topic and left with a much firmer grasp on it, and after sonarturtle I felt I could explain this to someone else without hesitation, that is the gold standard for any educational content and most sites simply fail to reach it ever which is unfortunate but true.

  2922. Robertniply

    Probably the kind of site that should be more widely read than it appears to be, and a look at elucan reinforced that quiet wish, the gap between a sites quality and its apparent reach is sometimes large and that gap exists for this site in a way that makes me want to mention it more.

  2923. AnthonyVah

    Skipped the comments section but might come back to read it, and a stop at ibacane hinted at a quality reader community, sites where the comments are worth reading separately from the post are increasingly rare and signal a particular kind of audience that has grown around the editorial vision over time gradually.

  2924. DaveZossy

    Well crafted post, the structure flows naturally from one point to the next without forcing transitions, and a stop at solosupple kept the same flow going, you can tell when a writer has thought about how their content reads rather than just what it contains and this is one of those examples.

  2925. Vivod iz zapoya na domy_oeKt

    Слушайте что расскажу. Столкнулся с такой бедой. Человек уже четвёртые сутки в штопоре. Жена в слезах. Платные клиники просят бешеные деньги. Короче, нормальные врачи нашлись — анонимный вывод из запоя без последствий. Отошёл за полчаса. В общем, смотрите сами по ссылке — выведение из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-samara-ghi.ru]выведение из запоя на дому[/url] Не тяните. Скиньте другу в беде.

  2926. Vivod iz zapoya na domy_gzsa

    Народ выручайте. Столкнулся с такой бедой. Человек уже пятые сутки в штопоре. Жена в слезах. Платные клиники просят бешеные деньги. Короче, нормальные врачи нашлись — профессиональное выведение из запоя капельницей. Приехали через час. В общем, там контакты и прайс — вывожу из запоя на дому самара [url=https://vyvod-iz-zapoya-na-domu-samara-abc.ru]https://vyvod-iz-zapoya-na-domu-samara-abc.ru[/url] Не надейтесь на авось. Перешлите тому кому надо.

  2927. Billytig

    Felt like the writer was speaking directly to someone with my level of curiosity, neither talking down nor showing off, and a stop at copperharborcommercegallery kept that comfortable matching going, finding writing that meets you where you are rather than asking you to climb up or stoop down feels great every time it happens.

  2928. SeanFoume

    Taking the time to read carefully here has been worthwhile for the past hour, and a look at lemonlarkartisanexchange extended the worthwhile reading, the calculation of return on reading time spent is something I do informally and this site has been producing positive returns across multiple sessions during the last week of regular visits and reads.

  2929. Vivod iz zapoya na domy_vcOl

    Самарцы всем привет. Попал я в переплёт конкретный. Человек уже седьмые сутки в штопоре. Соседи стучат в дверь. Платные клиники просят бешеные деньги. Короче, нормальные врачи нашлись — вывод из запоя дешево и сердито. Приехали через час. В общем, вся инфа вот здесь — наркология вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-samara-pqr.ru]https://vyvod-iz-zapoya-na-domu-samara-pqr.ru[/url] Не тяните. Скиньте другу в беде.

  2930. Pyblichnaya kadastrovaya karta_yyKl

    Ребята кто с недвижкой То вообще непонятно где смотреть Категория земли Короче, работает быстро и бесплатно — публичная кадастровая карта новая с 3D-видом Нашёл участок за 5 минут В общем, смотрите сами по ссылке — сайт публичной кадастровой карты [url=https://publichnaya-kadastrovaya-karta-abc.ru]https://publichnaya-kadastrovaya-karta-abc.ru[/url] Не мучайтесь с росреестром Перешлите тому кто ищет участок

  2931. Vivod iz zapoya na domy_tuka

    Слушайте что расскажу. Жесть случилась полная. Близкий не выходит из запоя. Жена в слезах. Платные клиники просят бешеные деньги. Короче, нормальные врачи нашлись — качественный вывод из запоя на дому. Поставили систему. В общем, там контакты и прайс — выведение из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-plk.ru]выведение из запоя на дому[/url] Каждая минута дорога. Перешлите тому кому надо.

  2932. Willissiz

    Thank you for the genuine effort here, it shows in every paragraph and not just the headline, and after my visit to biablur I was sure this site cares about getting things right rather than chasing clicks, which is the main reason I will come back later this week to read more.

  2933. JadonDweme

    Reading this confirmed that the topic deserves more careful attention than it usually gets, and a stop at crocusgrouse extended that elevated framing, content that raises the appropriate weight of a subject without being preachy about it is serving a quiet but important editorial function for the broader cultural conversation about it.

  2934. Pyblichnaya kadastrovaya karta_kvmr

    Народ кто с землёй Вечно то данные неактуальные Кадастровый номер вбить Короче, работает быстро и понятно — официальная публичная кадастровая карта с выписками Скачал выписку за секунду В общем, вся инфа вот здесь — публичной кадастровой карте росреестра [url=https://publichnaya-kadastrovaya-karta-ghi.ru]https://publichnaya-kadastrovaya-karta-ghi.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  2935. GarrettPable

    Decided to write a short note to the author if there is contact info anywhere, and a stop at bronzecrater extended that intention, the urge to thank the writer directly is a strong signal of content quality and this site has triggered that urge in me today which is a fairly rare event for my reading.

  2936. Ericknot

    Skipped breakfast still reading this and finished hungry but satisfied, and a stop at garnetcinder kept me past breakfast time, content that displaces basic biological needs is content with serious attentional pull and the writers here are clearly capable of producing that level of engagement which is genuinely impressive these days.

  2937. Jakeviath

    Really nice to see things explained without overcomplicating the topic, the words flow naturally and stay easy to follow, and a short visit to tunicvicar only added to that experience because the same simple approach is used across the rest of the page too without any change in tone.

  2938. LesterCib

    Reading this gave me a small mental break from the heavier reading I had been doing, and a stop at tealcovemerchantgallery extended that lighter feel, content that provides relief without becoming trivial is harder to produce than people realise and this site has clearly figured out how to be light without being shallow at all.

  2939. IgnacioNeago

    Reading this confirmed something I had been suspecting about the topic, and a look at falconbasil pushed that confirmation toward greater confidence, content that lines up with independently held intuitions earns a special kind of trust and I will return to writers who consistently land that way for me without overselling positions.

  2940. Cainrhymn

    Thank you for keeping the writing honest and the points easy to verify against your own experience, and a stop at sharesignal reflected the same approach, no exaggeration just steady useful content that I can take with me into my own work without second guessing every sentence I happen to read here.

  2941. SamsonMak

    Most of the time I bounce off similar pages within seconds, and a stop at chaletcobra held me longer than I would have predicted, the ability to convert a likely bouncing visitor into an engaged reader is a quality signal and this site has demonstrated that conversion ability across multiple visits where I expected to bounce.

  2942. TadGop

    Just want to record that this site is entering my regular reading list, and a look at jovigrove confirmed it deserves the spot, my regular reading list is short and well curated and adding to it requires meeting a fairly high quality bar that this site has clearly cleared without much effort apparently.

  2943. KurtDyepe

    Vague feelings of recognition kept surfacing as I read because the writing names things I have been thinking, and a look at shoreskipper produced more of those recognition moments, content that gives shape to private intuitions is content that makes me feel less alone in my own thinking and this site has that effect.

  2944. Vivod iz zapoya na domy_cyMn

    Слушайте что расскажу. Жесть случилась полная. Близкий не выходит из запоя. Жена в слезах. В диспансер везти — учёт на всю жизнь. Короче, единственное что реально помогло — вывод из запоя дешево и сердито. Отошёл за полчаса. В общем, сохраняйте на будущее — вывод из запоя на дому круглосуточно [url=https://vyvod-iz-zapoya-na-domu-samara-mno.ru]https://vyvod-iz-zapoya-na-domu-samara-mno.ru[/url] Каждая минута дорога. Перешлите тому кому надо.

  2945. Bartzolla

    Really like that there are no exclamation marks or all caps shouting throughout the post, and a quick visit to pineharbormerchantgallery maintained the same calm voice, restraint in punctuation signals confidence in the content and this site clearly trusts its substance to do the persuading rather than relying on typographic emphasis.

  2946. KalenMup

    Honestly informative, the writer covers the ground without showing off, and a look at urbanpickzone reflected the same humility, content that respects the reader rather than trying to dazzle them is something I always appreciate and rarely come across in this corner of the internet today across the topics I usually read.

  2947. Alvingrike

    Really nice to see things explained without overcomplicating the topic, the words flow naturally and stay easy to follow, and a short visit to cocoabasil only added to that experience because the same simple approach is used across the rest of the page too without any change in tone.

  2948. KalenAlale

    Picked this post to share in a Slack channel where I knew it would be appreciated, and a look at apronferret suggested I will share more from here later, content worth sharing into a professional context is content that has earned a higher kind of trust than mere personal interest and this site has it.

  2949. Vivod iz zapoya na domy_rjsi

    Ребята выручайте. Попал в жесть полную. Человек уже пятый день в штопоре. Соседи стучат в дверь. В диспансер везти — на всю жизнь учёт. Короче, единственное что реально помогло — доступный вывод из запоя цены адекватные. Примчались быстро. В общем, жмите чтобы не потерять — снятие запоя на дому [url=https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru]https://vyvod-iz-zapoya-na-domu-voronezh-eio.ru[/url] Не надейтесь на авось. Скиньте другу в беде.

  2950. Vivod iz zapoya na domy_peKt

    Слушайте что расскажу. Жесть случилась полная. Близкий не выходит из запоя. Дети не спят ночами. Скорая не едет. Короче, единственное что реально помогло — профессиональное выведение из запоя капельницей. Поставили систему. В общем, смотрите сами по ссылке — вывод из запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-samara-jkl.ru]вывод из запоя на дому цена[/url] Не тяните. Перешлите тому кому надо.

  2951. RufusGetty

    Felt a small spark of recognition when the post named something I had been struggling to articulate, and a look at hyxbrook produced more such moments, the rare service of giving readers language for fuzzy intuitions is one of the higher values that good writing can provide and this site offered several today instances.

  2952. Morgankix

    Came in skeptical of the angle and left mostly persuaded, and a stop at hollycattail pushed me a bit further in the same direction, content that can move a critical reader by argument rather than rhetoric is rare and worth pointing out because it indicates real substance underneath the surface presentation here.

  2953. Ginonus

    Really clear writing, the kind that makes you want to share the link with someone who has been asking about the topic, and a quick browse through turbantorso only made me more sure of that, the information here stays useful long after the first read is done which says a lot.

  2954. LewisElece

    Most blog writing on this subject reaches for the same handful of arguments and this post avoided them, and a look at ibekeg continued the original treatment, content that finds its own path through territory other writers have flattened is content with real authorial energy and this site has plenty of that distinctive energy.

  2955. RalphAdvaw

    Closed and reopened the tab three times before finally finishing, and a stop at beetledune held my attention straight through, sometimes content fights for time against my own distraction and the times it wins say something positive about its quality and this post clearly won that fight today afternoon for me.

  2956. Alexbug

    Top quality material, deserves more attention than it probably gets, and a look at emynox reflected the same effort across the site, a hidden gem in the modern web where most attention goes to whoever shouts loudest rather than whoever actually delivers the best content for their readers without much marketing fanfare.

  2957. MarcSak

    Just wanted to drop a quick note saying this was a useful read on a topic I have been circling, no fluff, and a stop at fawnfoxglove added a few extra points that fit the same simple style which makes the whole site feel coherent rather than thrown together by many different writers with different goals.

  2958. Vivod iz zapoya na domy_ltOl

    Народ выручайте. Попал я в переплёт конкретный. Муж просто пропадает. Жена в слезах. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — анонимный вывод из запоя без последствий. Отошёл за полчаса. В общем, жмите чтобы не потерять — вывод из запоя доктор на дом [url=https://vyvod-iz-zapoya-na-domu-samara-def.ru]https://vyvod-iz-zapoya-na-domu-samara-def.ru[/url] Каждая минута дорога. Скиньте другу в беде.

  2959. Vivod iz zapoya na domy_rhOl

    Слушайте что расскажу. Столкнулся с такой бедой. Брат пьёт без остановки. Дети не спят ночами. Платные клиники просят бешеные деньги. Короче, только это и спасло — вывод из запоя дешево и сердито. Отошёл за полчаса. В общем, смотрите сами по ссылке — выведение из запоя на дому нарколог [url=https://vyvod-iz-zapoya-na-domu-samara-pqr.ru]https://vyvod-iz-zapoya-na-domu-samara-pqr.ru[/url] Не надейтесь на авось. Скиньте другу в беде.

  2960. Vivod iz zapoya na domy_wsKt

    Слушайте что расскажу. Попал я в переплёт конкретный. Муж просто пропадает. Соседи стучат в дверь. В диспансер везти — учёт на всю жизнь. Короче, нормальные врачи нашлись — вывод из запоя дешево и сердито. Приехали через час. В общем, там контакты и прайс — вывод из запоя на дому в самаре [url=https://vyvod-iz-zapoya-na-domu-samara-ghi.ru]вывод из запоя на дому в самаре[/url] Не тяните. Перешлите тому кому надо.

  2961. Pyblichnaya kadastrovaya karta_pdKl

    Народ всем привет А в росреестре очереди Кадастровые номера и границы Короче, работает быстро и бесплатно — публичная кадастровая карта россии онлайн Скачал выписку сразу В общем, сохраняйте себе — карта с кадастровыми номерами [url=https://publichnaya-kadastrovaya-karta-abc.ru]https://publichnaya-kadastrovaya-karta-abc.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  2962. Reggieden

    After several visits I am now confident this site is one to follow seriously, and a stop at flonox reinforced that confidence, the gradual building of trust through repeated quality exposures is the only sustainable way to develop reader loyalty and this site is building that loyalty in me through patient consistent work consistently.

  2963. Edmundfes

    Pleasant surprise, the post delivered more than the headline promised, and a stop at lemonlarkcraftcollective continued that pattern of under promising and over delivering, the rarest combination on the modern web where most content does the opposite by promising the world and delivering thin recycled summaries instead each time you click on something interesting.

  2964. Ernestsox

    Recommended to anyone working in or curious about this area, the depth and clarity combine well, and a look at cypresselder keeps that going across more pages, the kind of site that earns regular visits rather than chasing trends has my respect because it suggests genuine commitment to the topic itself rather than to chasing trends.

  2965. Pyblichnaya kadastrovaya karta_mnmr

    Люди помогите То карта тормозит Категорию земли уточнить Короче, работает быстро и понятно — публичная кадастровая карта россии онлайн с обновлениями Скачал выписку за секунду В общем, там и карта и данные — кадастровая карта земли [url=https://publichnaya-kadastrovaya-karta-ghi.ru]https://publichnaya-kadastrovaya-karta-ghi.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  2966. Yusuffed

    Now sitting with the thoughts the post triggered rather than rushing on to the next thing, and a stop at elfinfennel extended that reflective pause, content that earns time for thought after closing the tab is content of higher value than the merely interesting and this site has clearly produced that lasting effect today.

  2967. Danstich

    Now feeling slightly more committed to my own careful reading practices having read this, and a stop at coralmeadowtradegallery reinforced that commitment, content that models the kind of attention it deserves is content that calibrates the reader and this site has clearly raised my own bar for what to bring to good writing today.

  2968. SullivanRoads

    Good post, the kind that respects the reader by getting to the point quickly without skipping the details that matter, and a short look at gentianfawn confirmed that approach is consistent across the site which is rare to find online these days, definitely a place I will return to soon.

  2970. Arnoldcrors

    Reading this brought back an idea I had set aside months ago, and a stop at salutesyrup added more substance to that idea, content that revives dormant projects in my own thinking is content with serious creative value and this site is contributing to my own work in ways I had not expected when first clicking through.

  2971. JamalEnefT

    Genuinely good work, the kind that holds up over multiple readings without losing its appeal, and a stop at falconbeetle kept that going, definitely a site I will be returning to and probably mentioning to others who work in or care about this particular area of interest today and in coming weeks.

  2972. Vernonhib

    Closed three other tabs to focus on this one and never opened them again, and a stop at timbertrailcommercegallery similarly held attention exclusively, content that crowds out other reading from working memory is content with real density and this site has demonstrated that density across multiple pages I have visited so far this morning.

  2973. Vivod iz zapoya na domy_nsMn

    Друзья ситуация. Жесть случилась полная. Брат пьёт без остановки. Соседи стучат в дверь. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — профессиональное выведение из запоя капельницей. Приехали через час. В общем, сохраняйте на будущее — доктор нарколог вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-samara-mno.ru]https://vyvod-iz-zapoya-na-domu-samara-mno.ru[/url] Не тяните. Скиньте другу в беде.

  2975. Aricip

    Decided to set aside time later to read more carefully, and a stop at bisonholly reinforced that decision, content that earns a calendar entry rather than just a passing read is in a different tier altogether and this site is clearly working at that elevated level which I really do appreciate as a reader today.

  2976. Vivod iz zapoya na domy_gnka

    Ребята всем привет. Попал я в переплёт. Человек уже четвёртые сутки в штопоре. Соседи стучат в дверь. Платные клиники просят бешеные деньги. Короче, нормальные врачи нашлись — срочный вывод из запоя круглосуточно. Поставили систему. В общем, сохраняйте на будущее — сколько стоит вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-voronezh-plk.ru]https://vyvod-iz-zapoya-na-domu-voronezh-plk.ru[/url] Не надейтесь на авось. Скиньте другу в беде.

  2979. DarrenDom

    Found this via a link from another piece I was reading and the click was worth it, and a stop at quartzmeadowcommercegallery extended the value across more material, the open web still rewards clicking through citations when the underlying writers care about each other work and this site clearly belongs to that network.

  2980. DeonRal

    A piece that did exactly what it promised in the headline without overshooting or underdelivering, and a look at dunecovemerchantgallery continued that calibration, alignment between promise and delivery is a basic editorial virtue that many sites fail at and this site has clearly mastered the matching of expectation and substance throughout pieces.

  2981. RonTeN

    Thank you for not assuming the reader already knows everything, the explanations meet me where I am, and a look at valuegoodsbazaar did the same, that consideration is what makes a site feel welcoming rather than gatekeepy which is sadly the default mood across the modern web today for most subjects covered.

  2986. KevinHew

    Glad I gave this a chance rather than scrolling past, and a stop at condoraspen confirmed I made the right call, sometimes the best content is hidden behind unassuming headlines that do not scream for attention and learning to slow down and check those out has paid off many times now across years of reading.

  2987. Percynum

    Halfway through I knew I would finish the post, and a stop at argylebasil also held me through to the end, content that signals its quality early and then sustains it is content with real internal consistency and this site has clearly figured out how to maintain quality from opening sentence through to closing thought.

  2988. WillieMug

    Now noticing how rare it is to find a site that does not feel rushed, and a look at icabran extended that calm pace, content produced without time pressure has a different quality than content shipped to meet a deadline and this site reads as written without urgency which produces a different and better experience for readers.

  2989. EanAquax

    Really appreciate this kind of writing, no shouting and no clickbait headlines just steady useful content, and a quick look at ilanub kept that going, definitely a site I will be returning to whenever I need a sensible take on similar topics in the days ahead and also during slower work weeks.

  2990. SonnyErync

    Now appreciating the way the post avoided the temptation to be longer than necessary, and a look at scarabsail continued that lean approach, content with the discipline to stop when finished rather than padding for length is content that respects both itself and its readers and this site has that disciplined editorial culture clearly throughout.

  2991. Pyblichnaya kadastrovaya karta_kfKl

    Ребята кто с недвижкой Вечно то данные устаревшие Кадастровые номера и границы Короче, нашел отличный инструмент — публичная кадастровая карта с поиском по номеру Скачал выписку сразу В общем, там и карта и данные — карта пкк [url=https://publichnaya-kadastrovaya-karta-abc.ru]https://publichnaya-kadastrovaya-karta-abc.ru[/url] Не мучайтесь с росреестром Перешлите тому кто ищет участок

  2992. Vivod iz zapoya na domy_hzOl

    Самарцы всем привет. Жесть случилась полная. Брат пьёт без остановки. Дети не спят ночами. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — анонимный вывод из запоя без последствий. Приехали через час. В общем, сохраняйте на будущее — запой врач на дом [url=https://vyvod-iz-zapoya-na-domu-samara-pqr.ru]https://vyvod-iz-zapoya-na-domu-samara-pqr.ru[/url] Не тяните. Скиньте другу в беде.

  2993. Cedrichiene

    Reading this gave me a small sense of progress on a topic I have been slowly working through, and a stop at borealgarnet added another step forward, learning happens in small increments across many sources and finding sources that consistently contribute is the actual practical value of careful curation in an information rich world.

  2994. Samsonprort

    Worth recommending broadly to anyone who reads on the topic, and a look at hollydragon only confirms that, the rare combination of accessibility and depth in this site makes it suitable for both newcomers and people who already know the area which is hard to pull off in any blog format today and rarely managed.

  2995. JimmyTip

    Took a chance on the headline and was rewarded, and a stop at bevelbison kept the rewards coming as I clicked through, the kind of place where every link leads somewhere worth the click is a small luxury on the modern web where so many sites are mostly empty calories disguised as content.

  2996. Jaimeamoni

    Reading this in pieces over a coffee break and finding it consistently rewarding, and a stop at bomboard extended that into related material I will return to later, the kind of site that fits naturally into small reading windows without requiring a long uninterrupted block is genuinely useful for how I actually browse.

  2997. Gerardosep

    Bookmark earned, share earned, return visit earned, all from one reading session, and a look at senatetoucan did the same, the trifecta of bookmark and share and return is rare in a single visit and represents the highest level of engagement I tend to offer any piece of online content these days here.

  2998. Jerrycob

    Skipped to a specific section because I knew that was the question I had, and the answer was clean, and a stop at eshcap similarly delivered targeted answers without burying them, content engineered for readers who arrive with specific needs rather than open ended browsing is increasingly valuable in a search heavy reading environment.

  2999. Vivod iz zapoya na domy_rjKt

    Слушайте что расскажу. Жесть случилась полная. Человек уже пятые сутки в штопоре. Жена в слезах. Скорая не едет. Короче, нормальные врачи нашлись — срочный вывод из запоя круглосуточно. Поставили систему. В общем, сохраняйте на будущее — вывод из запоя круглосуточно самара [url=https://vyvod-iz-zapoya-na-domu-samara-jkl.ru]вывод из запоя круглосуточно самара[/url] Каждая минута дорога. Скиньте другу в беде.

  3001. ErickDrobe

    My friends would appreciate a few of these posts and I will be sending links accordingly, and a look at dahliaferret added more pages to my share queue, content that earns shares to specific people in specific contexts is content with social utility and this site is generating those targeted shares from me consistently lately.

  3002. CoryLen

    Cuts through the usual marketing fluff that dominates this topic online, and a stop at floretbagel kept the same clean approach going, this is the kind of writing that respects the reader’s time rather than wasting it on repetitive setups before finally getting to the point at hand which is what most sites do.

  3003. Pyblichnaya kadastrovaya karta_tumr

    Народ кто с землёй Задолбался я уже искать нормальный сервис Категорию земли уточнить Короче, работает быстро и понятно — росреестр публичная кадастровая карта быстрый поиск Нашел всё за 10 минут В общем, сохраняйте себе — кадастровая карта россии 2025 [url=https://publichnaya-kadastrovaya-karta-ghi.ru]https://publichnaya-kadastrovaya-karta-ghi.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3004. Vivod iz zapoya na domy_xzMn

    Друзья ситуация. Жесть случилась полная. Близкий не выходит из запоя. Соседи стучат в дверь. В диспансер везти — учёт на всю жизнь. Короче, только это и спасло — вывод из запоя дешево и сердито. Поставили систему. В общем, жмите чтобы не потерять — вывод из запоя самара на дому [url=https://vyvod-iz-zapoya-na-domu-samara-mno.ru]https://vyvod-iz-zapoya-na-domu-samara-mno.ru[/url] Каждая минута дорога. Скиньте другу в беде.

  3005. Danaveld

    More substantial than most of what I find searching for this topic online, and a stop at geysercoyote kept that quality consistent, this is one of those sites where the writing actually rewards careful reading rather than punishing the patient reader with empty filler stretched out across long paragraphs that say very little.

  3007. Vivod iz zapoya na domy_arOl

    Народ выручайте. Столкнулся с такой бедой. Муж просто пропадает. Соседи стучат в дверь. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — профессиональное выведение из запоя капельницей. Отошёл за полчаса. В общем, жмите чтобы не потерять — снять запой на дому [url=https://vyvod-iz-zapoya-na-domu-samara-def.ru]https://vyvod-iz-zapoya-na-domu-samara-def.ru[/url] Не надейтесь на авось. Перешлите тому кому надо.

  3008. VirgilDag

    Saving the link for sure, this one is a keeper, and a look at steamsaunter confirmed I should bookmark the entire site rather than just this page, the consistency across what I have seen so far suggests there is a lot more here worth coming back for soon when I have more time.

  3009. KaiMah

    Now planning to recommend this site in a context where my recommendations are taken seriously, and a stop at linencoveartisanexchange confirmed I should make that recommendation soon, the small but real act of recommending content into spaces where my taste matters is something I take seriously and this site is worth the recommendation.

  3010. RossLaT

    A thoughtful read in a week that has been mostly noisy, and a look at holpod carried that thoughtful quality across more pages, finding pockets of considered writing in a week of distractions is one of the small wins of careful curation and this site is providing those pockets at a sustainable rate.

  3011. Charlesjaisa

    Following a few of the internal links revealed more posts of similar quality, and a stop at ferretcactus added more to that growing pile, sites where internal links lead to more good content rather than to more of the same recycled material are sites with depth and this one has clearly built that depth carefully.

  3012. Octavioamors

    A clear case of writing that does not try to do too much in one post, and a look at awningalmond maintained the same scoped discipline, posts that try to cover too much end up covering nothing well and this site has clearly chosen scope discipline as a core editorial principle which shows up clearly in what I read.

  3013. Fredericklag

    Skimmed first and then went back to read carefully, and the careful read paid off in places I had missed, and a stop at uplandharborcommercegallery got the same treatment, the rare site whose content rewards a second pass is content I want more of in my regular rotation rather than disposable single read articles.

  3014. Lewissuike

    More substantial than most of what I find searching for this topic online, and a stop at calicocopper kept that quality consistent, this is one of those sites where the writing actually rewards careful reading rather than punishing the patient reader with empty filler stretched out across long paragraphs that say very little.

  3015. Vivod iz zapoya na domy_ppKt

    Народ выручайте. Жесть случилась полная. Человек уже четвёртые сутки в штопоре. Дети не спят ночами. Скорая не едет. Короче, единственное что реально помогло — срочный вывод из запоя круглосуточно. Приехали через час. В общем, там контакты и прайс — вывод из запоя круглосуточно [url=https://vyvod-iz-zapoya-na-domu-samara-ghi.ru]вывод из запоя круглосуточно[/url] Не надейтесь на авось. Перешлите тому кому надо.

  3018. Leonardseemy

    If patience for careful reading is rare these days finding sites that reward it is rarer still, and a stop at harborstonevendorparlor extended that rare reward, the diminishing returns on shallow content reading have made me more selective about where to spend reading time and this site is meeting the higher selectivity bar consistently.

  3019. Pyblichnaya kadastrovaya karta_eyKl

    Ребята кто с недвижкой А в росреестре очереди Соседи какие Короче, нашел отличный инструмент — публичная кадастровая карта россии онлайн Увидел границы и соседей В общем, вся инфа вот здесь — кадастровая карата [url=https://publichnaya-kadastrovaya-karta-abc.ru]https://publichnaya-kadastrovaya-karta-abc.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3023. Vivod iz zapoya na domy_ihOl

    Народ выручайте. Столкнулся с такой бедой. Муж просто пропадает. Жена в слезах. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — профессиональное выведение из запоя капельницей. Поставили систему. В общем, вся инфа вот здесь — доктор нарколог вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-samara-pqr.ru]https://vyvod-iz-zapoya-na-domu-samara-pqr.ru[/url] Каждая минута дорога. Скиньте другу в беде.

  3025. Jacksonsween

    Now noticing the post fit a particular gap in my reading without my having articulated the gap before, and a look at quartzorchardmerchantgallery extended that gap filling effect, content that meets needs I had not consciously formulated is content with reader insight and this site has clearly developed that anticipatory editorial sense across many pieces.

  3026. Charliebib

    Reading this with my morning coffee turned into reading the related posts with my morning coffee, and a stop at affordableclothingshop stretched the morning further, content that pulls breakfast into a reading session rather than just accompanying it is content that has earned a higher claim on my attention than the average article does.

  3027. Pyblichnaya kadastrovaya karta_nmkr

    Здорово, народ Замучился я уже искать нормальный сервис Категорию земли уточнить Короче, работает быстро и понятно — публичная кадастровая карта новая с просмотром Скачал выписку за секунду В общем, сохраняйте себе — посмотреть кадастровую карту [url=https://publichnaya-kadastrovaya-karta-def.ru]посмотреть кадастровую карту[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3028. ClaytonTiete

    Found this via a link from another piece I was reading and the click was worth it, and a stop at condorferret extended the value across more material, the open web still rewards clicking through citations when the underlying writers care about each other work and this site clearly belongs to that network.

  3029. Pyblichnaya kadastrovaya karta_xaon

    Люди помогите То карта тормозит Категорию земли уточнить Короче, нашел крутой инструмент — публичная кадастровая карта россии онлайн с обновлениями Проверил обременения В общем, сохраняйте себе — публична кадастровая карта [url=https://publichnaya-kadastrovaya-karta-jkl.ru]публична кадастровая карта[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3030. VincentDok

    Without overstating it this is a quietly excellent post, and a look at idaoat extended that quiet excellence, content that earns superlatives without demanding them through marketing language is content that has truly earned them through the substance and this site has clearly produced work in that earned excellence category today.

  3031. Cliffordgophy

    Now wondering how the writers calibrated the level of detail so well, and a stop at treblevinca continued the same calibration, the right level of detail is one of the harder editorial calls in any piece and this site has clearly developed an instinct for it through what I assume is years of careful practice publicly.

  3032. HoracioLiemn

    Good quality through and through, no rough edges and no signs of being rushed, and a quick look at argylecougar kept the same polish going, the kind of site that respects its own brand by maintaining consistency across pages which is something I always appreciate as a reader looking for trustworthy information online today.

  3033. Germanimmet

    Skipped to a specific section because I knew that was the question I had, and the answer was clean, and a stop at ilobyte similarly delivered targeted answers without burying them, content engineered for readers who arrive with specific needs rather than open ended browsing is increasingly valuable in a search heavy reading environment.

  3034. ThomasUnmaw

    Really appreciate that the writer did not assume I would read every other related post first, and a look at camelferret kept that self contained feel going where each piece can stand alone, accessibility for new readers is a sign of generous editorial thinking and this site has clearly invested in that approach.

  3035. LiamHow

    Easy to recommend, the content speaks for itself without needing additional praise from me, and a stop at buckledahlia only adds more reasons to send people this way, the kind of generous resource that benefits its readers without demanding anything in return is increasingly rare and worth recognising clearly today across the broader open internet.

  3036. Vivod iz zapoya na domy_pqMn

    Слушайте что расскажу. Жесть случилась полная. Близкий не выходит из запоя. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, единственное что реально помогло — вывести из запоя на дому качественно. Поставили систему. В общем, жмите чтобы не потерять — вывод из запоя дешево самара [url=https://vyvod-iz-zapoya-na-domu-samara-mno.ru]https://vyvod-iz-zapoya-na-domu-samara-mno.ru[/url] Каждая минута дорога. Скиньте другу в беде.

  3037. Gregorybum

    Bookmark folder created specifically for this site, and a look at eshpyx confirmed the dedicated folder was the right call, dedicated folders for individual sites are a level of organisation I rarely deploy and this site has earned that level of dedicated tracking based on the consistency I have seen so far across sessions.

  3038. JayFolla

    Skipped the related links section thinking I had read enough and then came back to it later when curiosity got the better of me, and a stop at gypsyglider confirmed I should have just read it first, every section of this site appears to deserve careful attention rather than skipping past lazily.

  3039. Timgopay

    A piece that brought a sense of order to a topic I had been finding chaotic, and a look at hopperjaguar continued that organising effect, content that imposes useful structure on messy subjects is doing genuine intellectual work and this site is providing that organisational function across multiple posts I have read recently here.

  3040. LorenzoDeent

    Worth saying this site reads better than most paid newsletters I have tried, and a stop at daisybaron confirmed that comparison, the bar for free content is often lower than for paid but this site clears the paid bar consistently and that says something about the editorial approach behind the work being published here regularly.

  3041. Pyblichnaya kadastrovaya karta_nqmr

    Народ кто с землёй Задолбался я уже искать нормальный сервис Границы посмотреть Короче, нашел крутой инструмент — публичная кадастровая карта с 3D-видом Увидел границы и форму участка В общем, там и карта и данные — росреестр публичная кадастровая карта [url=https://publichnaya-kadastrovaya-karta-ghi.ru]https://publichnaya-kadastrovaya-karta-ghi.ru[/url] Не парьтесь с росреестром Перешлите тому кто ищет участок

  3042. LoganGuh

    Quality writing that respects the reader’s intelligence without overloading them, and a quick look at geyserdenim reflected that approach, a balanced thoughtful site that earns trust by being consistent rather than by shouting about how trustworthy it is which is the usual approach online sadly across most content categories.

  3043. BillyRew

    Closed the laptop after this and let the ideas settle for a few hours, and a stop at swamptweed similarly rewarded reflective time, content that benefits from sitting with rather than racing past is the kind I want more of and the kind that this site appears to consistently produce week after week here.

  3044. LoganSiz

    A piece that did not require external context to follow, and a look at suntansage maintained the same self contained quality, content that stands alone without forcing readers to chase prerequisites is more accessible and this site has clearly thought about how each piece can serve a fresh visitor rather than only existing members.

  3045. Jeffersonnum

    Liked the natural conversational tone throughout, never stiff and never overly casual either, and a stop at ferretglider kept that comfortable middle ground going, finding a tone that respects the reader without becoming distant or overly familiar is harder than it sounds and this site nails that balance consistently across many different pieces.

  3046. Ezekielzes

    Held my interest from the opening line through to the closing thought, and a stop at linencovecraftcollective did the same, content that earns sustained attention in an environment full of distractions is doing something right and this site is clearly doing several things right rather than just one or two which I really appreciate.

  3047. Bertbew

    Really appreciate this kind of writing, no shouting and no clickbait headlines just steady useful content, and a quick look at marbleharborcommercegallery kept that going, definitely a site I will be returning to whenever I need a sensible take on similar topics in the days ahead and also during slower work weeks.

  3048. Colbythogs

    Closed three other tabs to focus on this one and never opened them again, and a stop at wheatmeadowcommercegallery similarly held attention exclusively, content that crowds out other reading from working memory is content with real density and this site has demonstrated that density across multiple pages I have visited so far this morning.

  3049. Pyblichnaya kadastrovaya karta_euKl

    Народ всем привет А в росреестре очереди Соседи какие Короче, работает быстро и бесплатно — публичная кадастровая карта россии онлайн Увидел границы и соседей В общем, там и карта и данные — публичная кадастровая карта 2026 [url=https://publichnaya-kadastrovaya-karta-abc.ru]https://publichnaya-kadastrovaya-karta-abc.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3050. Vivod iz zapoya na domy_pvOl

    Друзья ситуация жуткая. Попал я в переплёт конкретный. Брат пьёт без остановки. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, нормальные врачи нашлись — вывести из запоя на дому качественно. Поставили систему. В общем, вся инфа вот здесь — снятие запоев на дому [url=https://vyvod-iz-zapoya-na-domu-samara-pqr.ru]https://vyvod-iz-zapoya-na-domu-samara-pqr.ru[/url] Не тяните. Перешлите тому кому надо.

  3051. Quincydiula

    Now thinking the topic is more interesting than I had given it credit for, and a stop at husbury continued that elevated interest, content that revives my curiosity about subjects I had set aside is doing genuine work in the structure of my interests and this site is providing that revivifying effect today actually.

  3052. Pyblichnaya kadastrovaya karta_agOa

    Слушайте кто участки ищет То вообще ничего не показывает Кадастровый номер вбить Короче, работает быстро и понятно — росреестр публичная кадастровая карта быстрый поиск Увидел границы и форму участка В общем, вся инфа вот здесь — открытая кадастровая карта россии [url=https://publichnaya-kadastrovaya-karta-mno.ru]https://publichnaya-kadastrovaya-karta-mno.ru[/url] Не парьтесь с росреестром Перешлите тому кто ищет участок

  3053. Pyblichnaya kadastrovaya karta_ewkr

    Здорово, народ А в росреестре очереди и бумажки Кадастровый номер вбить Короче, единственный сервис который не врет — росреестр публичная кадастровая карта быстрый поиск Увидел границы и форму участка В общем, сохраняйте себе — егрн 365 публичная кадастровая карта [url=https://publichnaya-kadastrovaya-karta-def.ru]егрн 365 публичная кадастровая карта[/url] Не парьтесь с росреестром Перешлите тому кто ищет участок

  3054. Pyblichnaya kadastrovaya karta_daon

    Люди помогите То вообще ничего не грузит Границы посмотреть Короче, единственный сервис который не врет — публичная кадастровая карта с 3D-видом Скачал выписку за секунду В общем, там и карта и данные — кадастровые карты [url=https://publichnaya-kadastrovaya-karta-jkl.ru]кадастровые карты[/url] Не парьтесь с росреестром Перешлите тому кто ищет участок

  3055. Howardvem

    Bookmark earned, calendar reminder set, share queued, all from one good post, and a look at cynbeo did the same, when a single reading session triggers multiple downstream actions you know the content has actually moved me beyond the page and this site is moving me at that higher level reliably.

  3056. JeffersonJoige

    Looking at the surface design and the substance together this site has both right, and a look at rainharbormerchantgallery reinforced that integrated quality, sites where presentation and content reinforce each other rather than fighting are sites with full editorial coherence and this one has clearly invested in both layers in a balanced way.

  3057. Steverep

    Bookmark folder reorganised slightly to make this site easier to find, and a look at copperburrow earned the same accessibility upgrade, the small organisational moves I make for sites I expect to return to often are themselves a signal of how much I trust them and this site triggered those moves naturally.

  3058. JudeShugs

    Reading this on a difficult day was a small bright spot, and a stop at allgoodsonline extended that brightness, content that improves a hard day is content that has earned a particular kind of place in my reading habits and this site is occupying that uplifting role for me today which I appreciate clearly.

  3059. Vivod iz zapoya na domy_hlMn

    Народ выручайте. Столкнулся с такой бедой. Близкий не выходит из запоя. Жена в слезах. Платные клиники просят бешеные деньги. Короче, только это и спасло — срочный вывод из запоя круглосуточно. Отошёл за полчаса. В общем, сохраняйте на будущее — вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-samara-mno.ru]вывод из запоя[/url] Каждая минута дорога. Перешлите тому кому надо.

  3060. DeonCigma

    My reading list is short and selective and this site is now on it, and a stop at cobblebadge confirmed the placement, the short list of sites I read deliberately rather than encounter accidentally is something I curate carefully and adding to it is a real act of trust which this site has earned today.

  3061. Orlandodreby

    Now feeling slightly more committed to my own careful reading practices having read this, and a stop at argylecrocus reinforced that commitment, content that models the kind of attention it deserves is content that calibrates the reader and this site has clearly raised my own bar for what to bring to good writing today.

  3062. Cecildancy

    Skipped breakfast still reading this and finished hungry but satisfied, and a stop at buntingdingo kept me past breakfast time, content that displaces basic biological needs is content with serious attentional pull and the writers here are clearly capable of producing that level of engagement which is genuinely impressive these days.

  3063. Franklinkic

    Now placing this in the small category of sites whose updates I would actually want to know about, and a stop at jebyam confirmed that placement, the difference between sites I want to follow and sites I just consume from is real and this one has crossed into the active follow category from the casual consumption side.

  3064. VictorWag

    Top tier post, the kind that makes you want to share the link with friends working in the same area, and a stop at tragustally only made me more confident in doing that, this site is one of the better resources I have seen on the topic recently across both new and older posts.

  3065. Kalebtep

    Bookmark earned and folder updated to track this site separately, and a look at daisydamson confirmed the folder upgrade was the right call, organising my reading list so that good sites do not get lost in a sea of casual bookmarks is something I do more carefully now and this site warranted its own spot.

  3066. Rileyslofe

    Closed the tab and immediately reopened it ten minutes later because I wanted to reread a part, and a stop at exabuff drew the same return, content that pulls you back after closing it is doing something well beyond the average and worth marking as exceptional in my mental catalogue of reliable sites.

  3067. MarkToodo

    My professional context would benefit from having this kind of resource available, and a look at junipercovegoodsgallery extended the professional applicability, the rare site that contributes meaningfully to professional work rather than just personal interest is content with multiplied value and this one is providing that professional utility consistently across multiple pieces.

  3068. LucasViesy

    Reading this back to back with a similar piece elsewhere made the quality difference obvious, and a stop at gingerfurrow only widened the gap, comparing content side by side is a useful exercise and the gap between this site and average competitors in the space is large enough to be noticeable from the first paragraph.

  3069. Vivod iz zapoya na domy_agOl

    Народ выручайте. Попал я в переплёт конкретный. Близкий не выходит из запоя. Жена в слезах. Скорая не едет. Короче, единственное что реально помогло — профессиональное выведение из запоя капельницей. Приехали через час. В общем, жмите чтобы не потерять — вывод из запоя самара [url=https://vyvod-iz-zapoya-na-domu-samara-def.ru]вывод из запоя самара[/url] Не тяните. Перешлите тому кому надо.

  3070. Pyblichnaya kadastrovaya karta_jwmr

    Слушайте кто участки смотрит А в росреестре ждать по три недели Кадастровый номер вбить Короче, нашел крутой инструмент — публичная кадастровая карта с 3D-видом Увидел границы и форму участка В общем, жмите чтобы не потерять — карта по кадастровому номеру [url=https://publichnaya-kadastrovaya-karta-ghi.ru]https://publichnaya-kadastrovaya-karta-ghi.ru[/url] Не парьтесь с росреестром Перешлите тому кто ищет участок

  3071. VincentFes

    Easy to recommend, the content speaks for itself without needing additional praise from me, and a stop at scarabvogue only adds more reasons to send people this way, the kind of generous resource that benefits its readers without demanding anything in return is increasingly rare and worth recognising clearly today across the broader open internet.

  3072. DallasHap

    Reading this on a long flight and finding it the best thing I read across hours of trying, and a stop at ibisglacier kept the streak going, when content beats long flight reading you know it has substance because flight reading is a hard test of a piece given the alternatives available everywhere.

  3073. Vivod iz zapoya na domy_lgKt

    Друзья ситуация жуткая. Жесть случилась полная. Близкий не выходит из запоя. Жена в слезах. Скорая не едет. Короче, единственное что реально помогло — вывести из запоя на дому качественно. Приехали через час. В общем, сохраняйте на будущее — срочный вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-samara-jkl.ru]срочный вывод из запоя на дому[/url] Не тяните. Скиньте другу в беде.

  3074. DavidCen

    Just want to acknowledge that the writing here is doing something right, and a quick visit to ferrethopper confirmed the same standards run across the broader site, recognising good work is something I try to do when I find it because the alternative is silence and silence rewards mediocrity.

  3075. Pyblichnaya kadastrovaya karta_dnKl

    Ребята кто с недвижкой А в росреестре очереди Соседи какие Короче, нашел отличный инструмент — публичная кадастровая карта россии онлайн Нашёл участок за 5 минут В общем, там и карта и данные — публичная кадастровая карта pkk [url=https://publichnaya-kadastrovaya-karta-abc.ru]https://publichnaya-kadastrovaya-karta-abc.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3076. Bernardalozy

    The structure of the post made it easy to follow without losing track of where I was, and a look at dingoholly kept the same logical flow going, this site clearly understands that organisation is half the battle in keeping readers engaged from the first line to the last across any kind of post.

  3077. Vivod iz zapoya na domy_izSn

    Друзья ситуация. Столкнулся с такой бедой. Человек уже вторые сутки в штопоре. Жена в слезах. В диспансер везти — учёт на всю жизнь. Короче, только это и спасло — вывод из запоя дешево и сердито. Поставили систему. В общем, смотрите сами по ссылке — вывод из запоя цены [url=https://vyvod-iz-zapoya-na-domu-samara-stu.ru]вывод из запоя цены[/url] Не тяните. Перешлите тому кому надо.

  3078. Vivod iz zapoya na domy_xyOl

    Народ выручайте. Жесть случилась полная. Близкий не выходит из запоя. Дети не спят ночами. Платные клиники просят бешеные деньги. Короче, только это и спасло — профессиональное выведение из запоя капельницей. Поставили систему. В общем, жмите чтобы не потерять — выведение из запоя на дому нарколог [url=https://vyvod-iz-zapoya-na-domu-samara-pqr.ru]https://vyvod-iz-zapoya-na-domu-samara-pqr.ru[/url] Не надейтесь на авось. Перешлите тому кому надо.

  3079. Pyblichnaya kadastrovaya karta_mfOa

    Люди подскажите А в росреестре очереди и бумажки Соседей проверить Короче, единственный сервис который не врет — росреестр публичная кадастровая карта быстрый поиск Проверил обременения В общем, жмите чтобы не потерять — публичная кадастровая карта российской федерации [url=https://publichnaya-kadastrovaya-karta-mno.ru]публичная кадастровая карта российской федерации[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3080. StanleyGer

    The examples really helped me grasp the points faster than abstract descriptions would have, and a stop at maplecrestartisanexchange added a few more practical illustrations that drove the message home, the kind of writing that knows its readers learn better through concrete situations rather than vague generalities is rare and worth recognising clearly.

  3081. GeoffreySyday

    Comfortable reading experience throughout, no jarring tone shifts and no awkward formatting, and a look at veilshore kept that smooth feel going, the kind of editorial polish that goes unnoticed when present but glaring when absent is something this site has clearly invested in across the broader content as well which deserves recognition.

  3084. Marshallblaro

    The lack of unnecessary jargon made the post accessible without sacrificing accuracy, and a look at hyxarch continued in the same accessible style, technical topics often hide behind specialised vocabulary but here the writer trusts the reader to keep up with plain language and that trust pays off nicely throughout the entire post.

  3085. Pyblichnaya kadastrovaya karta_knon

    Народ кто с недвижкой То вообще ничего не грузит Кадастровый номер вбить Короче, нашел крутой инструмент — публичная кадастровая карта новая с просмотром Нашел всё за 10 минут В общем, вся инфа вот здесь — публичный кадастровый реестр [url=https://publichnaya-kadastrovaya-karta-jkl.ru]публичный кадастровый реестр[/url] Не парьтесь с росреестром Перешлите тому кто ищет участок

  3086. Pyblichnaya kadastrovaya karta_dzkr

    Слушайте кто участки ищет Вечно то данные старые Категорию земли уточнить Короче, единственный сервис который не врет — публичная кадастровая карта новая с просмотром Проверил обременения В общем, вся инфа вот здесь — кадастровая карта нижегородская область [url=https://publichnaya-kadastrovaya-karta-def.ru]кадастровая карта нижегородская область[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3087. Riverwremi

    Picked this for my morning read because the topic seemed worth the time, and a look at cougararbor confirmed the choice was right, my morning reading slot is precious and giving it to this site felt like a good investment rather than a waste which is a higher endorsement than I usually offer for content.

  3088. HowardUsego

    Now considering writing a longer note about the post somewhere, and a look at bettercartmarket added more material for that note, content that prompts me to write rather than just consume is content with generative energy and this site is producing that generative effect for me at a higher rate than most sources.

  3089. Karlrog

    Even across multiple posts the writers voice has remained consistent in a way I appreciate, and a stop at elderchimney continued that voice, sites that maintain editorial consistency across many pieces have something most sites lack and this one has clearly worked out how to keep its voice steady across what reads as a growing archive.

  3090. Joseder

    I learned more from this short post than from longer articles I read earlier today, and a stop at ravensummitmerchantgallery added even more useful detail without going off topic, this site clearly knows how to keep things focused without sacrificing depth which is a hard balance to strike for any writer.

  3091. RickySloge

    This actually answered the question I had been searching for, and after I checked argylehopper I had a few more pieces I had not realised I needed, that is the sign of a site that knows what its readers want before they even know how to ask it which is impressive.

  3092. Vivod iz zapoya na domy_poMn

    Друзья ситуация. Столкнулся с такой бедой. Брат пьёт без остановки. Жена в слезах. Скорая не едет. Короче, только это и спасло — срочный вывод из запоя круглосуточно. Приехали через час. В общем, вся инфа вот здесь — запой вызов нарколога [url=https://vyvod-iz-zapoya-na-domu-samara-mno.ru]https://vyvod-iz-zapoya-na-domu-samara-mno.ru[/url] Каждая минута дорога. Скиньте другу в беде.

  3093. Eliasspafe

    After several visits I am now confident this site is one to follow seriously, and a stop at glacierglaze reinforced that confidence, the gradual building of trust through repeated quality exposures is the only sustainable way to develop reader loyalty and this site is building that loyalty in me through patient consistent work consistently.

  3094. Williambek

    Looking at this objectively the editorial quality is hard to deny even setting aside personal taste, and a stop at banyangeyser maintained the same objective quality, the gap between what I personally enjoy and what is objectively well crafted exists and this site clears both bars simultaneously which is rarer than it sounds.

  3095. RickCit

    The use of plain language without dumbing down the topic was really well done, and a look at burrowbrandy continued in that same accessible style, this is something many technical writers fail at because they either confuse their readers or condescend to them but here neither problem appears at all which is impressive really.

  3096. WalterHat

    Quiet confidence runs through the whole post, no need to shout to make the points stick, and a stop at daisyheron carried that same restrained voice forward, content that respects the reader by trusting its own substance rather than dressing it up in theatrical language is what I look for online and rarely actually find these days.

  3097. Calebgipse

    A welcome contrast to the loud takes that have dominated my feed lately, and a look at jedbroom extended that calm voice, content that arrives without yelling has become unusual in the modern attention economy and this site is one of the few places I have found that consistently delivers without raising its voice.

  3098. Chadcef

    Liked that the post resisted a sales pitch ending, and a stop at storkumber maintained the no pitch approach, content that ends without trying to convert me into a customer or subscriber is content that has confidence in its own value and this site is clearly playing the long game on reader trust.

  3099. Pyblichnaya kadastrovaya karta_lfKl

    Народ всем привет Замучился я уже искать информацию по участкам Кадастровые номера и границы Короче, нашел отличный инструмент — росреестр публичная кадастровая карта без глюков Проверил все данные В общем, смотрите сами по ссылке — публичная кадастровая карта новая [url=https://publichnaya-kadastrovaya-karta-abc.ru]https://publichnaya-kadastrovaya-karta-abc.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3100. Pyblichnaya kadastrovaya karta_gumr

    Народ кто с землёй То вообще ничего не грузит Соседей проверить Короче, нашел крутой инструмент — публичная кадастровая карта россии онлайн с обновлениями Нашел всё за 10 минут В общем, вся инфа вот здесь — кадастровый карта россии [url=https://publichnaya-kadastrovaya-karta-ghi.ru]кадастровый карта россии[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3101. ElijahWhace

    A piece that handled a controversial angle without becoming heated, and a look at ezabond continued that calm engagement, content that can address contested topics without inflaming them is doing rare diplomatic work and this site has clearly developed the editorial maturity to handle sensitive material with the appropriate temperature of writing throughout.

  3102. Vivod iz zapoya na domy_bgOl

    Слушайте что расскажу. Жесть случилась полная. Человек уже седьмые сутки в штопоре. Соседи стучат в дверь. Платные клиники просят бешеные деньги. Короче, только это и спасло — вывести из запоя на дому качественно. Поставили систему. В общем, сохраняйте на будущее — срочный вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-samara-pqr.ru]https://vyvod-iz-zapoya-na-domu-samara-pqr.ru[/url] Не надейтесь на авось. Скиньте другу в беде.

  3103. Sandypounc

    Worth your time, that is the simplest endorsement I can give, and a stop at mossharbormerchantgallery extends that endorsement across the rest of the site, this is one of those increasingly rare places that delivers on what it promises rather than over selling the content and under delivering on substance every time which I find frustrating elsewhere.

  3104. Fletcherdelve

    Reading this on a long flight and finding it the best thing I read across hours of trying, and a stop at ferretiguana kept the streak going, when content beats long flight reading you know it has substance because flight reading is a hard test of a piece given the alternatives available everywhere.

  3105. Pyblichnaya kadastrovaya karta_sqOa

    Слушайте кто участки ищет Задолбался я уже искать нормальный сервис Категорию земли уточнить Короче, нашел крутой инструмент — публичная кадастровая карта новая с просмотром Проверил обременения В общем, там и карта и данные — публичная карта рф [url=https://publichnaya-kadastrovaya-karta-mno.ru]https://publichnaya-kadastrovaya-karta-mno.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3106. Corytem

    Going to share this with a friend who has been asking the same questions for a while now, and a stop at iguanafjord added a few more pages I will pass along too, this is the kind of generous information that earns a small thank you from me right now and again later this week.

  3107. Vivod iz zapoya na domy_agSn

    Народ выручайте. Столкнулся с такой бедой. Человек уже вторые сутки в штопоре. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, только это и спасло — анонимный вывод из запоя без последствий. Отошёл за полчаса. В общем, там контакты и прайс — цена вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-samara-stu.ru]https://vyvod-iz-zapoya-na-domu-samara-stu.ru[/url] Не тяните. Перешлите тому кому надо.

  3108. Vivod iz zapoya na domy_cxKt

    Друзья ситуация жуткая. Жесть случилась полная. Муж просто пропадает. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, только это и спасло — анонимный вывод из запоя без последствий. Приехали через час. В общем, смотрите сами по ссылке — вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-samara-jkl.ru]вывод из запоя на дому[/url] Не надейтесь на авось. Перешлите тому кому надо.

  3109. HoseaTed

    Now placing this in the small category of sites whose updates I would actually want to know about, and a stop at drubeat confirmed that placement, the difference between sites I want to follow and sites I just consume from is real and this one has crossed into the active follow category from the casual consumption side.

  3110. Rogermogma

    Reading this on a difficult day was a small bright spot, and a stop at lavenderharborvendorparlor extended that brightness, content that improves a hard day is content that has earned a particular kind of place in my reading habits and this site is occupying that uplifting role for me today which I appreciate clearly.

  3112. Pyblichnaya kadastrovaya karta_ufon

    Люди помогите А в росреестре ждать по три недели Категорию земли уточнить Короче, работает быстро и понятно — публичная кадастровая карта россии онлайн с обновлениями Увидел границы и форму участка В общем, там и карта и данные — публичная кадастровая карта москва [url=https://publichnaya-kadastrovaya-karta-jkl.ru]https://publichnaya-kadastrovaya-karta-jkl.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3113. Pyblichnaya kadastrovaya karta_rqkr

    Слушайте кто участки ищет Замучился я уже искать нормальный сервис Категорию земли уточнить Короче, работает быстро и понятно — росреестр публичная кадастровая карта быстрый поиск Нашел всё за 10 минут В общем, жмите чтобы не потерять — кадастровый номер на карте [url=https://publichnaya-kadastrovaya-karta-def.ru]кадастровый номер на карте[/url] Не парьтесь с росреестром Перешлите тому кто ищет участок

  3114. AlfredoPex

    The depth of coverage felt about right for the format, neither shallow nor overwhelming, and a look at gumbofeather kept that calibration going, getting the depth right for blog format is genuinely difficult because too shallow loses experts and too deep loses beginners but this site nailed it nicely which I really do appreciate.

  3117. EddiePeM

    A piece that suggested careful editing without showing the marks of the editing, and a look at cougarfloret continued that invisible polish, the best editing disappears into the prose and this site reads as having been edited with skill that does not announce itself which is the highest compliment I can offer any blog content.

  3119. HassanAdomb

    A small thing but the line spacing and font choices made reading this physically pleasant, and a look at buyareashop maintained the same careful design, technical choices about typography are part of what makes online reading actually comfortable and this site has clearly invested in the design layer alongside the content layer carefully.

  3121. WalkerViers

    Following the post through to the end without my attention drifting once, and a look at rivercovemerchantgallery earned the same uninterrupted attention, content that holds attention without manipulating it is content with substantive pull and this site has demonstrated that substantive pull across multiple pieces in a single reading session reliably here today.

  3122. JudeMes

    During the time spent here I noticed the absence of the usual distractions, and a stop at armorhedge extended that distraction free experience, content that does not fight my attention with pop ups and modals and aggressive prompts is content that respects me and this site has clearly chosen the respectful approach throughout.

  3123. TroyBit

    Thanks for taking the time to write this, it is clear that some thought went into how each point would land, and after I went through cobraboulder I had a better grip on the topic, real value without the usual marketing noise people have to put up with online when searching for answers.

  3124. KaneDoure

    A slim post with substantial content per word, and a look at suburbvesper maintained the same density, the content per word ratio is something I track informally and this site scores high on that ratio compared to most sources I read regularly which is a quiet indicator of careful editorial work behind the scenes.

  3125. YaleRep

    Appreciate the thoughtful approach, the writer clearly took time to make this readable for someone who is not already an expert, and a look at damsoncamel kept that going nicely, easy on the eyes and easy on the brain which is always a winning combination when reading on a busy day.

  3126. PrincePeami

    Even from a single post the editorial care is clear, and a stop at ibecap extended that care across more pages, the kind of attention to quality that shows up in every paragraph is what separates serious sites from the rest and this one has clearly invested in that paragraph level attention across what I have read.

  3127. BeauOvala

    Now noticing that the post never raised its voice even when making a strong point, and a look at burstferret continued that calm volume, content that can make important points without resorting to typographic emphasis or emotional appeal is content that trusts its substance to do the work and this site has that confidence consistently.

  3129. Lylecoups

    Decided to subscribe to the RSS feed if there is one, and a stop at triggersyrup confirmed that decision, content that I want delivered to me proactively rather than just remembered when I have time is content that has earned a higher level of commitment from me as a reader looking for reliable sources.

  3130. Pyblichnaya kadastrovaya karta_isOa

    Привет, народ А в росреестре очереди и бумажки Кадастровый номер вбить Короче, работает быстро и понятно — публичная кадастровая карта новая с просмотром Скачал выписку за секунду В общем, вся инфа вот здесь — кадастровая карта участков [url=https://publichnaya-kadastrovaya-karta-mno.ru]https://publichnaya-kadastrovaya-karta-mno.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3131. Pyblichnaya kadastrovaya karta_exmr

    Люди помогите Задолбался я уже искать нормальный сервис Кадастровый номер вбить Короче, нашел крутой инструмент — публичная кадастровая карта россии онлайн с обновлениями Увидел границы и форму участка В общем, вся инфа вот здесь — егрн карта [url=https://publichnaya-kadastrovaya-karta-ghi.ru]https://publichnaya-kadastrovaya-karta-ghi.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3132. Pyblichnaya kadastrovaya karta_sbKl

    Ребята кто с недвижкой То сайты виснут Кадастровые номера и границы Короче, нашел отличный инструмент — публичная кадастровая карта новая с 3D-видом Проверил все данные В общем, смотрите сами по ссылке — публичная карта россии [url=https://publichnaya-kadastrovaya-karta-abc.ru]публичная карта россии[/url] Не мучайтесь с росреестром Перешлите тому кто ищет участок

  3133. Marcustop

    Top tier post, the kind that makes you want to share the link with friends working in the same area, and a stop at fescuefalcon only made me more confident in doing that, this site is one of the better resources I have seen on the topic recently across both new and older posts.

  3134. Codysal

    Reading this on a slow Sunday and finding it perfectly suited to a slow Sunday read, and a quick stop at faearo kept the same gentle pace, content that fits the mood of the moment is something I notice and remember and this site has the kind of pace that suits relaxed reading sessions especially well.

  3135. Vivod iz zapoya na domy_vxOl

    Самарцы всем привет. Столкнулся с такой бедой. Близкий не выходит из запоя. Дети не спят ночами. Платные клиники просят бешеные деньги. Короче, только это и спасло — профессиональное выведение из запоя капельницей. Поставили систему. В общем, там контакты и прайс — вывод из запоя дешево [url=https://vyvod-iz-zapoya-na-domu-samara-pqr.ru]вывод из запоя дешево[/url] Каждая минута дорога. Скиньте другу в беде.

  3136. JaxonSib

    Found a couple of useful angles in here I had not considered before reading carefully, and a quick stop at dunebuckle added more, this is one of those sites where the value compounds the more you read rather than peaking at one viral post and then offering nothing else of substance afterwards which is common.

  3137. FabianSap

    Honestly thank you to whoever wrote this because it scratched an itch I had not quite been able to articulate, and a stop at unifiednexus kept that satisfying feeling going, the kind of writing that meets unspoken needs is special and this site clearly has writers who understand their readers more than most do today.

  3138. BrandonCheap

    Honestly impressed by how much useful content sits in such a small post, and a stop at careervertex confirmed the rest of the site packs a similar punch, density without confusion is a hard balance to strike and this site has clearly cracked the code on it across many different topic areas covered.

  3139. Darnellmus

    Honestly this hits the sweet spot between detail and brevity, no rambling and no shortcuts, and a quick visit to singlevision kept that going across the related pages, the kind of place that respects your attention without trying to grab it through cheap tactics or attention seeking design choices that get tired fast.

  3140. CarmeloFug

    If I were to recommend a starting point for the topic this site would be near the top of my list, and a stop at cameranexus reinforced that recommendation status, the small list of starting point recommendations I keep for friends asking about topics is short and this site is now firmly on it.

  3141. Derrickpeaph

    A well calibrated piece that knew its scope and stayed inside it, and a look at impaladenim maintained the same scope discipline, scope creep is one of the failure modes of long blog posts and this site has clearly invested in the editorial discipline to prevent it which shows up in tightly contained pieces.

  3142. Connornuame

    Refreshing to read something where the words actually mean something instead of filling space, and a stop at streamnexushub kept that going, the writing here trusts the reader to follow along without endless repetition or constant reminders of what was already said earlier in the post which I appreciate.

  3143. Walterteale

    Now noticing that the post never raised its voice even when making a strong point, and a look at brightamigo continued that calm volume, content that can make important points without resorting to typographic emphasis or emotional appeal is content that trusts its substance to do the work and this site has that confidence consistently.

  3144. RossNeaws

    Bookmark added with a small mental note that this is a site to keep, and a look at brightwinner reinforced the keep status, the verb keep rather than visit captures something about how I think about this kind of site and it is a higher tier of relationship than I have with most places online today.

  3145. Vivod iz zapoya na domy_nwSn

    Друзья ситуация. Столкнулся с такой бедой. Муж просто пропадает. Дети не спят ночами. Скорая не едет. Короче, только это и спасло — срочный вывод из запоя круглосуточно. Отошёл за полчаса. В общем, там контакты и прайс — лечение запоев на дому [url=https://vyvod-iz-zapoya-na-domu-samara-stu.ru]лечение запоев на дому[/url] Не надейтесь на авось. Перешлите тому кому надо.

  3146. Pyblichnaya kadastrovaya karta_pukr

    Люди подскажите Вечно то данные старые Границы посмотреть Короче, нашел крутой инструмент — официальная публичная кадастровая карта с выписками Проверил обременения В общем, жмите чтобы не потерять — онлайн кадастровая карта [url=https://publichnaya-kadastrovaya-karta-def.ru]https://publichnaya-kadastrovaya-karta-def.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3147. Pyblichnaya kadastrovaya karta_zoon

    Слушайте кто участки смотрит Задолбался я уже искать нормальный сервис Категорию земли уточнить Короче, единственный сервис который не врет — публичная кадастровая карта с 3D-видом Нашел всё за 10 минут В общем, вся инфа вот здесь — публичной кадастровой картой росреестра [url=https://publichnaya-kadastrovaya-karta-jkl.ru]https://publichnaya-kadastrovaya-karta-jkl.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3148. Vivod iz zapoya na domy_frKt

    Самарцы всем привет. Попал я в переплёт конкретный. Муж просто пропадает. Жена в слезах. Скорая не едет. Короче, нормальные врачи нашлись — анонимный вывод из запоя без последствий. Отошёл за полчаса. В общем, жмите чтобы не потерять — вывод из запоя на дому самара круглосуточно [url=https://vyvod-iz-zapoya-na-domu-samara-jkl.ru]вывод из запоя на дому самара круглосуточно[/url] Не надейтесь на авось. Скиньте другу в беде.

  3149. Devinmot

    Useful reading material, the kind I can hand off to someone newer to the topic without worrying about confusing them, and a quick look at coyotecarbon confirmed the same beginner friendly tone runs throughout the site which is great for sharing with people just starting their learning journey on this particular topic.

  3151. WileyHeP

    Definitely a recommend from me, anyone curious about the topic should check this out, and a look at dappleburrow adds even more reason for that, the depth and quality combine to make this site one I will be pointing people toward whenever similar conversations come up over the months ahead at work or socially.

  3152. Pyblichnaya kadastrovaya karta_xcOa

    Привет, народ А в росреестре очереди и бумажки Категорию земли уточнить Короче, единственный сервис который не врет — официальная публичная кадастровая карта с выписками Проверил обременения В общем, вся инфа вот здесь — новая кадастровая карта [url=https://publichnaya-kadastrovaya-karta-mno.ru]https://publichnaya-kadastrovaya-karta-mno.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3153. Willisred

    Now wishing more sites covered topics with this level of care, and a look at ascotbison extended that wish across more subjects, the rarity of careful coverage on most topics is a problem and this site is one of the small antidotes to that broader pattern of casual or surface treatment of complex subjects.

  3154. RobinBlemi

    A clean piece that knew exactly what it wanted to say and said it, and a look at pearlcovemerchantgallery maintained the same clarity of intention, knowing the goal of a piece before writing is something most blog content lacks and the clarity of purpose here shows up in every paragraph for any careful reader to notice.

  3155. AbrahamSem

    Now thinking about how to apply some of this to a project I have been planning, and a look at riverharborcommercegallery added more material for the planning, content that connects to my actual creative work rather than just being interesting in the abstract is the kind that earns priority placement in my reading rotation consistently going forward.

  3156. TonyTwica

    Bookmark added with a small note about why, and a look at butteaspen prompted another bookmark with another note, the bookmarks I annotate are the ones I expect to return to deliberately rather than stumble into and this site is generating annotated bookmarks at a higher rate than my usual content sources by some margin.

  3157. Taylornog

    Reading this gave me confidence to make a decision I had been putting off, and a stop at targetskein reinforced that confidence, content that translates into action in my own life rather than just informing it is content with the highest practical value and this site is generating that action level utility for me lately.

  3158. JeremyDak

    Reading this confirmed that my time researching the topic in other places had not been wasted, and a stop at balsacougar extended the confirmation, when independent sources agree that is a useful signal and this site is one of the more reliable sources I have found for cross checking what I read elsewhere on similar subjects.

  3159. CordellRic

    Such writing is increasingly rare and worth supporting through attention, and a stop at fescuegarnet extended that supportive attention across more pages, the conscious choice to spend time on sites that produce careful work rather than convenient consumption is itself a small form of patronage and this site is receiving that conscious patronage from me.

  3160. DuanePhype

    Worth saying that the post fit naturally into a rhythm of careful reading, and a stop at idequa extended the same rhythm, content that pairs well with how I actually read rather than demanding a different mode is content well calibrated to its likely audience and this site has clearly thought about that consistently.

  3161. MartinSwaks

    Reading this back to back with a similar piece elsewhere made the quality difference obvious, and a stop at faelex only widened the gap, comparing content side by side is a useful exercise and the gap between this site and average competitors in the space is large enough to be noticeable from the first paragraph.

  3162. DwaynePirty

    Thank you for keeping the writing honest and the points easy to verify against your own experience, and a stop at primevertexhub reflected the same approach, no exaggeration just steady useful content that I can take with me into my own work without second guessing every sentence I happen to read here.

  3163. LawrenceNal

    If quality blog writing is dying as people sometimes claim then this site is one piece of evidence that it has not died yet, and a look at skillvoyager extended that evidence, the broader cultural question about online writing has empirical answers in specific sites and this one is contributing to a more optimistic answer overall.

  3164. StefanKic

    Now thinking about how this post will age over the coming years, and a stop at growthvertexhub suggested the same durability, content built to age well rather than to capture the attention of the moment is content with a different kind of value and this site has clearly chosen the long horizon over the short one.

  3165. CamdenCix

    Looking through other posts here the consistency is what makes the site valuable rather than any single piece, and a stop at urbanfamilia extended that consistency observation, sites whose value lies in the ongoing pattern rather than in standout posts are sites I trust more deeply and this one has clearly built that kind of trust.

  3166. NathanLat

    Solid value packed into a relatively short post, that takes skill, and a look at writerharbor continues the dense useful content across more pages, this site clearly understands that respecting reader time is itself a form of generosity which is something most blog operations seem to have forgotten lately across the wider open web.

  3167. Franklinesoni

    Looking at the surface design and the substance together this site has both right, and a look at trancetidal reinforced that integrated quality, sites where presentation and content reinforce each other rather than fighting are sites with full editorial coherence and this one has clearly invested in both layers in a balanced way.

  3168. NedTredy

    Coming to this with low expectations and being pleasantly surprised by the substance, and a stop at deliverynexus continued exceeding expectations, the recalibration of expectations upward across multiple positive readings is one of the actual rewards of careful browsing and this site is providing that recalibration at a steady rate apparently.

  3169. Bjornstast

    A small editorial detail caught my attention, the way headings related to body text, and a look at tritonsloop maintained that careful relationship, structural details like that show up to readers who notice them and the writers here have clearly thought about every level of the piece rather than just the words.

  3170. LaineSkich

    Honest opinion is that this is the kind of post that builds long term trust with readers, and a look at royalmariner reinforced that perception, the slow accumulation of trust through consistent quality is the only sustainable way to build a real audience and this site is clearly playing that long game.

  3171. Raulbroow

    Came away with a slightly better mental model of the topic than I started with, and a stop at orientnexus sharpened that further, content that improves the reader thinking apparatus rather than just dumping facts into it is the rare kind I genuinely value and seek out when I have time to read carefully.

  3172. JackPax

    Looking for similar voices elsewhere has come up empty in my recent searches, and a stop at masteryvertex extended the search frustration, the rare site that does what no other does in quite the same way is precious and this one has clearly developed a particular approach that I have not been able to find duplicates of.

  3173. Pyblichnaya kadastrovaya karta_cumr

    Слушайте кто участки смотрит То вообще ничего не грузит Границы посмотреть Короче, нашел крутой инструмент — публичная кадастровая карта россии онлайн с обновлениями Увидел границы и форму участка В общем, вся инфа вот здесь — карта егрн [url=https://publichnaya-kadastrovaya-karta-ghi.ru]https://publichnaya-kadastrovaya-karta-ghi.ru[/url] Не парьтесь с росреестром Перешлите тому кто ищет участок

  3174. NelsonneT

    Now planning to come back when I have the right kind of attention to read carefully, and a stop at glaciergourd reinforced that plan, choosing the right moment to read certain content is a quiet form of respect for the work and this site is generating those careful planning behaviours from me consistently as a reader.

  3175. Pyblichnaya kadastrovaya karta_ason

    Народ кто с недвижкой Вечно то данные неактуальные Категорию земли уточнить Короче, единственный сервис который не врет — публичная кадастровая карта россии онлайн с обновлениями Скачал выписку за секунду В общем, там и карта и данные — росреестр кадастровая карта [url=https://publichnaya-kadastrovaya-karta-jkl.ru]росреестр кадастровая карта[/url] Не парьтесь с росреестром Перешлите тому кто ищет участок

  3176. Pyblichnaya kadastrovaya karta_aikr

    Ребята кто с землей Вечно то данные старые Категорию земли уточнить Короче, нашел крутой инструмент — публичная кадастровая карта с 3D-видом Проверил обременения В общем, жмите чтобы не потерять — карта реестра [url=https://publichnaya-kadastrovaya-karta-def.ru]карта реестра[/url] Не парьтесь с росреестром Перешлите тому кто ищет участок

  3177. Pyblichnaya kadastrovaya karta_zvOa

    Люди подскажите А в росреестре очереди и бумажки Категорию земли уточнить Короче, единственный сервис который не врет — публичная кадастровая карта новая с просмотром Увидел границы и форму участка В общем, вся инфа вот здесь — кадастровый реестр карта [url=https://publichnaya-kadastrovaya-karta-mno.ru]https://publichnaya-kadastrovaya-karta-mno.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3178. Sylvestercix

    Picked something concrete from the post that I will use immediately, and a look at goldencovemerchantgallery added another concrete piece, content that produces immediately useful output rather than just abstract appreciation is content that earns its place in my regular rotation without needing any further evaluation from me at this point honestly.

  3179. Vivod iz zapoya na domy_qpSn

    Самарцы привет. Жесть случилась полная. Муж просто пропадает. Соседи стучат в дверь. Скорая не едет. Короче, единственное что реально помогло — вывод из запоя дешево и сердито. Приехали через час. В общем, сохраняйте на будущее — врач вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-samara-stu.ru]врач вывод из запоя[/url] Не надейтесь на авось. Скиньте другу в беде.

  3180. Jeffersonsop

    Picked something concrete from the post that I will use immediately, and a look at coyotederby added another concrete piece, content that produces immediately useful output rather than just abstract appreciation is content that earns its place in my regular rotation without needing any further evaluation from me at this point honestly.

  3181. Marshallroand

    Recommended to anyone working in or curious about this area, the depth and clarity combine well, and a look at dapplecondor keeps that going across more pages, the kind of site that earns regular visits rather than chasing trends has my respect because it suggests genuine commitment to the topic itself rather than to chasing trends.

  3182. KnoxKak

    Held my interest from the opening line through to the closing thought, and a stop at aspenalmond did the same, content that earns sustained attention in an environment full of distractions is doing something right and this site is clearly doing several things right rather than just one or two which I really appreciate.

  3183. Jasonabats

    Different in a good way from the cookie cutter content that fills most blogs covering this area, and a stop at byncane kept showing me why, original thoughtful writing exists if you know where to look and this site has earned a place on my short list of those rare exceptions worth defending.

  3184. KalBlire

    Closed three other tabs to focus on this one and never opened them again, and a stop at buttecanoe similarly held attention exclusively, content that crowds out other reading from working memory is content with real density and this site has demonstrated that density across multiple pages I have visited so far this morning.

  3185. Vivod iz zapoya na domy_ogKt

    Народ выручайте. Попал я в переплёт конкретный. Брат пьёт без остановки. Дети не спят ночами. Платные клиники просят бешеные деньги. Короче, нормальные врачи нашлись — анонимный вывод из запоя без последствий. Отошёл за полчаса. В общем, жмите чтобы не потерять — вывести из запоя недорого на дому [url=https://vyvod-iz-zapoya-na-domu-samara-jkl.ru]вывести из запоя недорого на дому[/url] Не надейтесь на авось. Скиньте другу в беде.

  3186. BrandonCheap

    Reading this confirmed something I had been suspecting about the topic, and a look at careervertex pushed that confirmation toward greater confidence, content that lines up with independently held intuitions earns a special kind of trust and I will return to writers who consistently land that way for me without overselling positions.

  3188. Timmytar

    Took me back a step or two on an assumption I had been making, and a stop at ebonycanyon pushed that reconsideration further, writing that gently corrects the reader without being aggressive about it is a rare diplomatic skill and the team here clearly knows how to land critical points without turning readers off.

  3189. Nedtrulk

    Worth saying that the writing carries a particular kind of authority without making any explicit claims to it, and a stop at fescueimpala extended that earned authority feeling, sites that demonstrate expertise through the quality of their explanations rather than by stating credentials are sites I trust most and this site has it.

  3190. Sandydoogy

    Picked up on several small touches that suggest a careful editor, and a look at borealberyl suggested the same hand at work across the broader site, editorial consistency at a granular level is one of the strongest signs that an operation is serious rather than just hobbyist and this site reads as serious throughout.

  3191. Calvintig

    Started forming counter examples to test the claims and the post handled most of them implicitly, and a look at falbell continued that anticipatory style, writers who think two steps ahead of the critical reader save themselves from a lot of follow up work and this writer has clearly internalised that habit consistently.

  3193. Pyblichnaya kadastrovaya karta_pbOa

    Привет, народ Вечно то данные старые Границы посмотреть Короче, единственный сервис который не врет — публичная кадастровая карта с 3D-видом Проверил обременения В общем, вся инфа вот здесь — кадастровый карта россии [url=https://publichnaya-kadastrovaya-karta-mno.ru]кадастровый карта россии[/url] Не парьтесь с росреестром Перешлите тому кто ищет участок

  3194. Cartercah

    A piece that handled the topic with appropriate weight without becoming portentous, and a look at a478884 continued that calibrated seriousness, content that takes itself seriously without becoming pompous is something this site has clearly figured out and the balance shows up in every piece I have read across multiple sessions now.

  3195. Pyblichnaya kadastrovaya karta_oyon

    Всем привет из сети То вообще ничего не грузит Соседей проверить Короче, нашел крутой инструмент — публичная кадастровая карта россии онлайн с обновлениями Увидел границы и форму участка В общем, сохраняйте себе — пкк онлайн [url=https://publichnaya-kadastrovaya-karta-jkl.ru]пкк онлайн[/url] Не парьтесь с росреестром Перешлите тому кто ищет участок

  3196. Pyblichnaya kadastrovaya karta_dkkr

    Здорово, народ Замучился я уже искать нормальный сервис Границы посмотреть Короче, работает быстро и понятно — публичная кадастровая карта с 3D-видом Проверил обременения В общем, там и карта и данные — кадастровая карта онлайн бесплатно [url=https://publichnaya-kadastrovaya-karta-def.ru]кадастровая карта онлайн бесплатно[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3197. Dennisamomy

    Found something quietly useful here that I expect to return to, and a stop at derbycobra added more of the same, content with quiet utility ages well in a way that flashy hot takes do not and I have learned to weight quiet utility much higher when deciding what to bookmark for later use.

  3199. JimmyPet

    Looking for similar voices elsewhere has come up empty in my recent searches, and a stop at coyotehopper extended the search frustration, the rare site that does what no other does in quite the same way is precious and this one has clearly developed a particular approach that I have not been able to find duplicates of.

  3200. Robertpoove

    Came away with a small but real shift in perspective on the topic, and a stop at cadbrisk pushed that shift a bit further, the kind of subtle reframing that good writing does to a reader without making a big deal of it is something I always appreciate when it happens which is sadly not that often.

  3201. Vivod iz zapoya na domy_cjSn

    Народ выручайте. Попал я в переплёт конкретный. Близкий не выходит из запоя. Жена в слезах. В диспансер везти — учёт на всю жизнь. Короче, нормальные врачи нашлись — анонимный вывод из запоя без последствий. Отошёл за полчаса. В общем, жмите чтобы не потерять — вывод из запоя самара на дому [url=https://vyvod-iz-zapoya-na-domu-samara-stu.ru]вывод из запоя самара на дому[/url] Не надейтесь на авось. Скиньте другу в беде.

  3202. Leonardedism

    If you asked me to point to a recent positive sign for the open web this site would be near the top, and a stop at tomatotactic reinforced that designation, the few sites that serve as evidence the web can still produce quality independent content are precious and this one has clearly become one for me.

  3203. TonyUnfip

    Reading this prompted me to dig into a related topic later, and a stop at granitegrovecommercegallery provided some of the starting points for that follow up reading, content that triggers further exploration rather than satisfying curiosity completely is content with real generative energy and this site has plenty of that energy throughout it.

  3204. JohanVog

    Took the time to read every paragraph rather than skimming for the punchline, and a quick visit to aspenclipper earned the same careful attention from me, that is the highest signal I can give about content quality because my default mode is rapid scanning rather than deliberate reading on most pages.

  3205. KeaganCribe

    Thanks for the simple approach, too many sites bury the actual point under layers of unnecessary words, but here every line earns its place, and a look at cactusferret showed the same care for the reader which is something I will remember the next time I need answers on a topic.

  3206. BrandonCheap

    Came back to this twice now in the same week which is unusual for me, and a look at careervertex suggested I will keep coming back, the kind of post that earns repeated visits rather than one and done reading is the gold standard for content quality and this site clearly hit that standard.

  3208. DavionAtmox

    Just want to flag that this was useful and not bury the appreciation in caveats, and a look at fjordalmond earned the same direct praise, recognising good work without hedging it with criticism is something I try to practice because over qualified compliments tend to read as backhanded and miss the point sometimes.

  3209. Pyblichnaya kadastrovaya karta_ppOa

    Люди подскажите Задолбался я уже искать нормальный сервис Соседей проверить Короче, работает быстро и понятно — росреестр публичная кадастровая карта быстрый поиск Проверил обременения В общем, вся инфа вот здесь — карта земельного кадастра [url=https://publichnaya-kadastrovaya-karta-mno.ru]https://publichnaya-kadastrovaya-karta-mno.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3210. GermanGlymn

    Looking through other posts here the consistency is what makes the site valuable rather than any single piece, and a stop at falpyx extended that consistency observation, sites whose value lies in the ongoing pattern rather than in standout posts are sites I trust more deeply and this one has clearly built that kind of trust.

  3211. ArchCrara

    Quietly enjoying that I have found a new site to follow for the topic, and a look at gumboacorn reinforced the small pleasure of the find, the discovery of new high quality sources is one of the more durable pleasures of careful internet reading and this site has been generating that discovery pleasure at multiple points already today.

  3212. Pyblichnaya kadastrovaya karta_bnon

    Люди помогите Вечно то данные неактуальные Соседей проверить Короче, работает быстро и понятно — публичная кадастровая карта россии онлайн с обновлениями Скачал выписку за секунду В общем, вся инфа вот здесь — открытая карта росреестра [url=https://publichnaya-kadastrovaya-karta-jkl.ru]открытая карта росреестра[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3213. Pyblichnaya kadastrovaya karta_uckr

    Ребята кто с землей А в росреестре очереди и бумажки Границы посмотреть Короче, единственный сервис который не врет — публичная кадастровая карта новая с просмотром Проверил обременения В общем, там и карта и данные — публичная кадастровая карта бесплатно [url=https://publichnaya-kadastrovaya-karta-def.ru]https://publichnaya-kadastrovaya-karta-def.ru[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3214. Vivod iz zapoya na domy_ysMi

    Народ выручайте. Попал я в переплёт конкретный. Близкий не выходит из запоя. Дети не спят ночами. Платные клиники просят бешеные деньги. Короче, только это и спасло — профессиональное выведение из запоя капельницей. Приехали через час. В общем, там контакты и прайс — выведение из запоя на дому нарколог [url=https://vyvod-iz-zapoya-na-domu-samara-vwx.ru]https://vyvod-iz-zapoya-na-domu-samara-vwx.ru[/url] Не тяните. Скиньте другу в беде.

  3215. Vivod iz zapoya na domy_gssl

    Народ выручайте. Столкнулся с такой бедой. Человек уже четвёртые сутки в штопоре. Жена в слезах. Скорая не едет. Короче, только это и спасло — анонимный вывод из запоя без последствий. Приехали через час. В общем, жмите чтобы не потерять — вывод из запоя доктор на дом [url=https://vyvod-iz-zapoya-na-domu-samara-yza.ru]https://vyvod-iz-zapoya-na-domu-samara-yza.ru[/url] Не надейтесь на авось. Скиньте другу в беде.

  3216. ErvinTeelf

    A piece that handled multiple complications without becoming confused, and a look at diamondbasil continued that organisational clarity, holding multiple threads in a single piece without losing any of them is a sign of skilled writing and this site has clearly developed the editorial discipline to manage complexity without sacrificing readability throughout.

  3217. HoseaEdino

    If I had encountered this site five years ago I would have been telling everyone about it, and a look at stitchstudio extended that retrospective enthusiasm, the version of me who used to recommend favourite blogs frequently would have made sure friends knew about this one and that earlier enthusiasm is partially returning to me here.

  3218. Ronnieununc

    Honestly impressed by how much useful content sits in such a small post, and a stop at cobqix confirmed the rest of the site packs a similar punch, density without confusion is a hard balance to strike and this site has clearly cracked the code on it across many different topic areas covered.

  3219. RodneyMam

    Got pulled in by the headline and stayed because the content actually delivered on the promise, and a stop at crateranchor kept that trust intact, when a site lives up to its own framing it earns the right to keep showing up in my browser tabs going forward indefinitely from here on out really.

  3220. Bryanvef

    Just wanted to drop a quick note saying this was a useful read on a topic I have been circling, no fluff, and a stop at cactusgumbo added a few extra points that fit the same simple style which makes the whole site feel coherent rather than thrown together by many different writers with different goals.

  3221. DanielNah

    Really appreciate this kind of writing, no shouting and no clickbait headlines just steady useful content, and a quick look at barleybuckle kept that going, definitely a site I will be returning to whenever I need a sensible take on similar topics in the days ahead and also during slower work weeks.

  3222. LawrenceNal

    Just one of those reads that left me feeling slightly more capable rather than overwhelmed, and a look at skillvoyager kept that empowering feel going, the difference between content that builds the reader up and content that intimidates them is huge and this site clearly knows which side of that line to stand.

  3223. Vivod iz zapoya na domy_kySn

    Слушайте что расскажу. Попал я в переплёт конкретный. Брат пьёт без остановки. Жена в слезах. Скорая не едет. Короче, нормальные врачи нашлись — вывести из запоя на дому качественно. Поставили систему. В общем, жмите чтобы не потерять — вывод из запоя на дому в самаре [url=https://vyvod-iz-zapoya-na-domu-samara-stu.ru]вывод из запоя на дому в самаре[/url] Не надейтесь на авось. Скиньте другу в беде.

  3224. AshtonCor

    One of the more honest takes on the topic I have seen lately, no spin and no oversell, and a stop at borealelfin kept that going, the kind of voice the open web could use a lot more of rather than the endless echo chamber of recycled opinions floating around every social platform these days.

  3225. Sidneydok

    Now feeling slightly more committed to my own careful reading practices having read this, and a stop at graniteorchardmerchantgallery reinforced that commitment, content that models the kind of attention it deserves is content that calibrates the reader and this site has clearly raised my own bar for what to bring to good writing today.

  3226. OctavioDer

    A particular kind of restraint shows up in the writing, and a look at acorndamson maintained the same restraint across pages, knowing what not to say is just as important as knowing what to say and this site has clearly developed strong instincts on both sides of that editorial line throughout pieces I have read.

  3227. Pyblichnaya kadastrovaya karta_xgOa

    Слушайте кто участки ищет Задолбался я уже искать нормальный сервис Категорию земли уточнить Короче, работает быстро и понятно — публичная кадастровая карта россии онлайн с обновлениями Проверил обременения В общем, смотрите сами по ссылке — публичная карта егрн [url=https://publichnaya-kadastrovaya-karta-mno.ru]публичная карта егрн[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3228. MarcosSlild

    Now considering carefully how to share this site with the right audience rather than broadcasting widely, and a look at fjordaster extended that careful sharing impulse, content worth sharing carefully rather than spamming is content that has earned a higher kind of recommendation and this site has earned that careful shareability throughout pieces.

  3229. Vivod iz zapoya na domy_suMi

    Народ выручайте. Столкнулся с такой бедой. Муж просто пропадает. Дети не спят ночами. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — профессиональное выведение из запоя капельницей. Поставили систему. В общем, жмите чтобы не потерять — нарколог вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-samara-vwx.ru]нарколог вывод из запоя[/url] Не тяните. Скиньте другу в беде.

  3230. Nicholaswer

    Now thinking about whether the writer might publish a longer form work I would buy, and a look at joxaxis suggested the same depth would translate, content that makes me want to pay for related work in other formats is content that has earned commercial trust as well as attention trust and this site has both clearly.

  3231. Alfredopoict

    A piece that did not lecture even when it had clear positions, and a look at brindledingo maintained the same teaching without preaching tone, finding the line between informing and lecturing is hard and most sites land on the wrong side of it but this one has clearly figured out how to inform without becoming preachy.

  3232. JackAvoiz

    Worth recognising the absence of the usual blog tropes here, and a look at dingoalmond continued that fresh quality, sites that avoid the standard moves of the medium read as more original even when the content is on familiar topics and this one has clearly chosen its own path through the conventional terrain skilfully.

  3233. 888starz_cder

    يُعد الموقع الرسمي 888starz في مصر منصة رائدة للكازينو والرهانات الرياضية تجمع كل الخدمات في مكان واحد.
    تُعرض أحدث ألعاب السلوت والعناوين الأكثر شعبية في مقدمة صفحة الكازينو.
    تتوفر احتمالات قوية ورهان مباشر مع متابعة فورية للنتائج والإحصائيات.
    تسجيل دخول 888 [url=http://www.egypt888stars.com]https://egypt888stars.com/[/url]
    تظهر جميع العروض والمكافآت بوضوح على الموقع الرسمي لتسهيل الاستفادة منها.
    يعمل الدعم الفني على مدار الساعة باللغتين العربية والإنجليزية عبر الدردشة والبريد والهاتف.

  3234. 888starz_cbsa

    يدعم الموقع اللغة العربية وطرق دفع مناسبة للسوق المصري لضمان تجربة مريحة.

    يحتوي كازينو 888starz على أكثر من 5000 لعبة من كبار المزودين مثل Pragmatic Play و NetEnt و Microgaming.

    يتميز الموقع بأودز تنافسية وخيارات رهان حي مع تحديث لحظي للاحتمالات أثناء المباريات.

    يحصل المستخدمون الجدد على مكافأة ترحيب حتى 1500 يورو إضافة إلى 150 فري سبين.

    يوفر 888starz تسجيلًا سريعًا عبر رقم الهاتف أو الإيميل أو خيار النقرة الواحدة.

    888starz [url=http://cars.yclas.com/user/williamhansen9/]https://cars.yclas.com/user/williamhansen9[/url]

  3235. CooperSex

    Reading this between meetings turned out to be the most useful thing I did all afternoon, and a stop at fibdot kept that productivity feeling going, content can sometimes outperform actual work in terms of what gets accomplished mentally and this site managed that today which is genuinely a high bar to clear consistently.

  3236. Vivod iz zapoya na domy_gbsl

    Народ выручайте. Жесть случилась полная. Близкий не выходит из запоя. Соседи стучат в дверь. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — профессиональное выведение из запоя капельницей. Приехали через час. В общем, жмите чтобы не потерять — вывод из запоя цены самара [url=https://vyvod-iz-zapoya-na-domu-samara-yza.ru]https://vyvod-iz-zapoya-na-domu-samara-yza.ru[/url] Не тяните. Перешлите тому кому надо.

  3237. Kylepodia

    Refreshing to find writing that does not try to manipulate the reader into clicking onto the next page through cliffhangers and forced engagement, and a stop at cratercopper continued in the same respectful way, this is what reader first design actually looks like in practice rather than just in marketing copy that sounds nice.

  3238. JeffersonSog

    Started imagining how I would explain the topic to someone else after reading, and a look at vaultvalue gave me more material for that imagined explanation, content that improves my own ability to discuss a topic is content that has actually transferred knowledge rather than just decorating my screen for a few minutes.

  3239. 888starz_glEr

    888 stars [url=http://www.mybluegreece.com/888-starz-%d9%85%d8%b5%d8%b1-%d8%a7%d9%84%d9%85%d9%88%d9%82%d8%b9-%d8%a7%d9%84%d8%b1%d8%b3%d9%85%d9%8a-%d9%84%d9%84%d9%83%d8%a7%d8%b2%d9%8a%d9%86%d9%88-%d9%88%d8%a7%d9%84%d9%85%d8%b1%d8%a7%d9%87%d9%86]https://mybluegreece.com/888-starz-%d9%85%d8%b5%d8%b1-%d8%a7%d9%84%d9%85%d9%88%d9%82%d8%b9-%d8%a7%d9%84%d8%b1%d8%b3%d9%85%d9%8a-%d9%84%d9%84%d9%83%d8%a7%d8%b2%d9%8a%d9%86%d9%88-%d9%88%d8%a7%d9%84%d9%85%d8%b1%d8%a7%d9%87%d9%86/[/url]
    يتوفر الموقع باللغة العربية مع خيارات إيداع وسحب ملائمة للمستخدمين المصريين.

    تتوفر احتمالات قوية على معظم البطولات مما يزيد من قيمة الرهانات.

    يضم الموقع مجموعة واسعة من ألعاب السلوت والروليت والبلاك جاك من شركات رائدة.

    يُنصح دائمًا بمراجعة شروط العروض وتحديد ميزانية واللعب بمسؤولية.

  3240. Jacobglazy

    Will be sharing this with a couple of people who care about the topic, and a stop at brightframeshub added more material worth passing along, the kind of site that is generous with quality content and does not make you jump through hoops to access it which is appreciated more than the team probably realises.

  3241. Bertrambic

    Worth a quiet moment of recognition for the consistency I have noticed across multiple posts, and a stop at barniguana continued that consistent quality, sites that maintain quality across many pieces rather than peaking on one viral post are sites with real editorial discipline and this one has clearly developed that discipline carefully.

  3242. Wilsonkeeno

    A piece that exhibited the kind of patience that good writing requires, and a look at canoebeech continued that patient quality, hurried writing is easy to spot and this site reads as having been written without time pressure which produces a different feel than the rushed content that dominates much of the modern blog space.

  3243. crazytime_drKi

    Crazy Time rappresenta uno dei game show dal vivo più amati nei casinò online.
    crazytime demo [url=gsiani01.nayaa.co.kr/bbs/board.php?bo_table=sub04_01&wr_id=119152]https://gsiani01.nayaa.co.kr/bbs/board.php?bo_table=sub04_01&wr_id=119152[/url]
    I quattro bonus sono Cash Hunt, Pachinko, Coin Flip e il celebre Crazy Time.
    Il Top Slot aggiunge moltiplicatori che possono trasformare una puntata in una grande vincita.
    Giocare con consapevolezza e definire un budget aiuta a vivere l’esperienza in sicurezza.

  3245. Vivod iz zapoya na domy_djki

    Народ выручайте. Жесть случилась полная. Брат пьёт без остановки. Жена в слезах. Скорая не едет. Короче, нормальные врачи нашлись — вывести из запоя на дому качественно. Приехали через час. В общем, там контакты и прайс — вывод из запоя частный врач [url=https://vyvod-iz-zapoya-na-domu-samara-bcd.ru]https://vyvod-iz-zapoya-na-domu-samara-bcd.ru[/url] Не тяните. Скиньте другу в беде.

  3246. 888_mkkt

    يخضع 888starz لمعايير صارمة تضمن شفافية اللعب وحماية المعلومات الشخصية.
    starz888 [url=https://www.uniprint.co.kr/bbs/board.php?bo_table=free&wr_id=305504/]https://uniprint.co.kr/bbs/board.php?bo_table=free&wr_id=305504[/url]
    يحتوي 888starz على مكتبة واسعة من ألعاب الكازينو من شركات برمجيات موثوقة.

    يدعم الموقع المراهنة الحية مع بث للنتائج وتغير الأودز في الوقت الفعلي.

    يقدم الموقع للاعبين المصريين الجدد مكافأة ترحيب تغطي الكازينو والرياضة معًا.

    ينبه التطبيق اللاعبين بالأحداث الرياضية والمكافآت الجديدة بشكل فوري.

  3247. 888starz_amSa

    888starz rasmiy sayti O’zbekistonda kazino o’yinlari va sport tikishlarini bitta platformada birlashtiradi.
    Top reytingli va yangi chiqqan slot o’yinlari saytda alohida ajratib beriladi.
    888starz. [url=https://www.888-uz8.com/]https://888-uz8.com/[/url]
    Jonli tikish rejimi o’yin davomida koeffitsiyentlarni real vaqtda yangilab boradi.
    Yangi o’yinchilar uchun 888starz birinchi depozitga ulkan xush kelibsiz bonusini taqdim etadi.
    Yangi hisob yaratish telefon, email yoki bir tugma orqali tez va oson bajariladi.

  3248. Pyblichnaya kadastrovaya karta_kokr

    Здорово, народ Замучился я уже искать нормальный сервис Соседей проверить Короче, нашел крутой инструмент — публичная кадастровая карта россии онлайн с обновлениями Нашел всё за 10 минут В общем, там и карта и данные — публична кадастровая карта росреестр [url=https://publichnaya-kadastrovaya-karta-def.ru]публична кадастровая карта росреестр[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3249. Pyblichnaya kadastrovaya karta_pyon

    Люди помогите То карта тормозит Соседей проверить Короче, нашел крутой инструмент — публичная кадастровая карта новая с просмотром Скачал выписку за секунду В общем, вся инфа вот здесь — росреестр пкк [url=https://publichnaya-kadastrovaya-karta-jkl.ru]росреестр пкк[/url] Пользуйтесь нормальной картой Перешлите тому кто ищет участок

  3250. ______fbSl

    تحميل 888starz [url=http://www.divisionmidway.org/jobs/author/georgeill/]https://divisionmidway.org/jobs/author/georgeill/[/url]
    ????? ??? apk ?????? 888starz ??????? ??????? ??? ????? ??????? ??????.

    ??? ????? ????? ???? ????? ???? ??????? ?????? ????? ??????? ????????.

    ???? ??????? ??? ??????? ?????? ????? ??? ???????? ?????? ??? ???????.

    ????? ?????? ???????? ???? ?????? ??????? ??? ????? ????? ???????.

    ???? ????? iOS ??? ???? ???? ??????? ?? ????? ?????? ?????? ???.

  3251. Vivod iz zapoya na domy_jwSn

    Друзья ситуация. Попал я в переплёт конкретный. Муж просто пропадает. Жена в слезах. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — вывод из запоя дешево и сердито. Приехали через час. В общем, сохраняйте на будущее — анонимный вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-samara-stu.ru]анонимный вывод из запоя[/url] Не тяните. Скиньте другу в беде.

  3252. 888starz_xrSa

    Sayt qulay navigatsiya bilan bo’limlar o’rtasida tez almashish imkonini beradi.
    бк 888starz [url=http://www.888-uz9.com]https://888-uz9.com/[/url]
    O’yin va aksiyalar haqidagi bildirishnomalar foydalanuvchiga ilova orqali yetkaziladi.
    Rasmiy platforma har bir to’lov amaliyotini kuchli xavfsizlik qatlamlari bilan ta’minlaydi.
    888starz rasmiy litsenziya asosida ishlaydi va adolatli o’yinni kafolatlaydi.

  3253. Miguelsem

    Now realising the post solved a small problem I had been carrying for weeks, and a look at hazelharborcommercegallery extended that problem solving function, content that connects to specific unresolved questions in my own life rather than just providing general interest is content with real practical impact and this site is providing that practical value.

  3254. 888starz_hjSa

    888starz rasmiy platformasi o’zbek tilini qo’llab-quvvatlaydi va sodda dizaynga ega.

    888starz rasmiy sayti slot, ruletka va blekjek kabi mingdan ortiq kazino o’yinini taklif etadi.

    Rasmiy sayt orqali O’zbekiston ligasi va xalqaro chempionatlarga tikish mumkin.

    Rasmiy sayt orqali hisobni to’ldirish va yechib olish bir necha usulda amalga oshiriladi.
    888starz betting [url=https://888starz-uzb1.com/]https://888starz-uzb1.com/[/url]

  3255. Vivod iz zapoya na domy_ceMi

    Народ выручайте. Попал я в переплёт конкретный. Брат пьёт без остановки. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, нормальные врачи нашлись — анонимный вывод из запоя без последствий. Поставили систему. В общем, вся инфа вот здесь — вывод из запоя врач на дом [url=https://vyvod-iz-zapoya-na-domu-samara-vwx.ru]вывод из запоя врач на дом[/url] Не надейтесь на авось. Перешлите тому кому надо.

  3256. Jorgenob

    Worth saying that the prose reads naturally without straining for style, and a stop at adobebronze maintained the same unforced quality, writing that achieves elegance without effort is the highest tier and this site has clearly worked out how to land that effortless quality consistently rather than only on the writers best days.

  3257. 888starz_zoOt

    888starz official website [url=https://888starz-uzb2.com/]888starz official website[/url].
    888starz rasmiy platformasi o’zbek foydalanuvchilariga kazino va tikishlarni bir joyda jamlaydi.
    Yangi va ommabop o’yinlar rasmiy saytning kazino bo’limida birinchi bo’lib ko’rsatiladi.
    Rasmiy sayt orqali mahalliy va xalqaro chempionatlarga, jumladan O’zbekiston ligasiga tikish mumkin.
    Rasmiy sayt litsenziyalangan bo’lib, o’yinchilar uchun xavfsiz va adolatli muhitni kafolatlaydi.

  3258. ArnoldoBog

    Closed the tab feeling I had spent the time well, and a stop at fjordchimney extended that feeling across more pages, the test of whether time on a site was well spent is one I apply silently after closing tabs and very few sites pass it but this one passed it cleanly today afternoon clearly.

  3259. MalcolmNitle

    Looking at this objectively the editorial quality is hard to deny even setting aside personal taste, and a stop at dingocypress maintained the same objective quality, the gap between what I personally enjoy and what is objectively well crafted exists and this site clears both bars simultaneously which is rarer than it sounds.

  3260. BarryNab

    Decided not to skim despite my usual habit and was rewarded for the discipline, and a stop at flyburn earned the same patient approach, training myself to recognise sites that warrant slower reading is part of being a careful online reader and this site is the kind that helps me practice that skill regularly.

  3261. CamdenTus

    Recommended without reservation for anyone interested in the topic at any level of expertise, and a look at craterglider only strengthens that recommendation, this site clearly knows how to serve readers across a range of backgrounds without watering down the content or talking past anyone in the audience which is genuinely impressive to see.

  3262. Garyvient

    Comfortable in tone and substantive in content, that is a hard combination to land, and a look at autovoyager kept that pairing alive across more material, this is what good editorial direction looks like in practice and the team here clearly has someone keeping a steady hand on the wheel across what they decide to publish.

  3263. CarmineNit

    During a reading session that included several other sources this one stood out, and a look at canyonbobcat continued the standout quality, the side by side comparison of sources during research is a useful exercise and this site has been winning those comparisons for me consistently across multiple research sessions during the last week.

  3264. Vivod iz zapoya na domy_ohki

    Народ выручайте. Попал я в переплёт конкретный. Близкий не выходит из запоя. Соседи стучат в дверь. Платные клиники просят бешеные деньги. Короче, нормальные врачи нашлись — вывести из запоя на дому качественно. Поставили систему. В общем, сохраняйте на будущее — вывод из запоя на дому самара цены [url=https://vyvod-iz-zapoya-na-domu-samara-bcd.ru]https://vyvod-iz-zapoya-na-domu-samara-bcd.ru[/url] Каждая минута дорога. Перешлите тому кому надо.

  3265. MitchellJam

    Granted my mood today might be elevating my reading experience but I still think this is genuinely good, and a stop at baronbarley reinforced that even discounted assessment, controlling for the mood adjustment that affects content perception this site still reads as substantively above average across multiple pieces I have read carefully today.

  3266. Mathewneern

    Decided after reading this that I would check this site weekly going forward, and a stop at dragonebony reinforced that commitment, deciding to add a site to a regular rotation requires meeting a quality bar that very few places clear and this one cleared it cleanly without any noticeable effort or marketing push behind it.

  3267. Vivod iz zapoya na domy_kiKt

    Народ выручайте. Столкнулся с такой бедой. Человек уже пятые сутки в штопоре. Жена в слезах. Скорая не едет. Короче, только это и спасло — вывод из запоя дешево и сердито. Приехали через час. В общем, там контакты и прайс — вывод из запоя цена на дому [url=https://vyvod-iz-zapoya-na-domu-samara-jkl.ru]вывод из запоя цена на дому[/url] Не тяните. Скиньте другу в беде.

  3268. Kelvinbow

    Honest take is that I will probably forget most of what I read online today but this post is one I will remember, and a stop at jadejetty kept that same memorable quality going, certain writing leaves a residue in the mind in a way most content simply does not manage.

  3269. Vivod iz zapoya na domy_zysl

    Самарцы привет. Столкнулся с такой бедой. Брат пьёт без остановки. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, нормальные врачи нашлись — вывести из запоя на дому качественно. Приехали через час. В общем, смотрите сами по ссылке — вывод из запоя цена [url=https://vyvod-iz-zapoya-na-domu-samara-yza.ru]вывод из запоя цена[/url] Каждая минута дорога. Перешлите тому кому надо.

  3270. Vivod iz zapoya na domy_qlMi

    Народ выручайте. Попал я в переплёт конкретный. Брат пьёт без остановки. Дети не спят ночами. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — вывести из запоя на дому качественно. Приехали через час. В общем, там контакты и прайс — вывести из запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-samara-vwx.ru]https://vyvod-iz-zapoya-na-domu-samara-vwx.ru[/url] Не тяните. Перешлите тому кому надо.

  3271. Juliocot

    Felt like I was reading something written by someone who actually thinks about the topic rather than reciting it, and a look at kyarax reinforced that impression, the difference between recited content and considered content is huge and this site clearly belongs to the latter category which I appreciate as a careful reader looking for substance.

  3272. Vivod iz zapoya na domy_rgSn

    Народ выручайте. Столкнулся с такой бедой. Муж просто пропадает. Жена в слезах. В диспансер везти — учёт на всю жизнь. Короче, нормальные врачи нашлись — вывод из запоя дешево и сердито. Приехали через час. В общем, смотрите сами по ссылке — вывод из запоя на дому в самаре [url=https://vyvod-iz-zapoya-na-domu-samara-stu.ru]вывод из запоя на дому в самаре[/url] Не тяните. Скиньте другу в беде.

  3274. JermaineGromy

    Beats most of the alternatives on the topic by a noticeable margin, and a look at honeymeadowcommercegallery did not change that at all, this is one of the better corners of the open internet for this kind of content and I am glad I clicked through rather than skipping past quickly like I usually do.

  3275. Arthurrax

    Reading this slowly in the morning before opening email, and a stop at elmwoodgumbo extended that protected attention, content that earns the prime morning reading slot before the daily distractions begin is content with elevated status and this site has earned that prime slot consistently in my recent reading habits clearly.

  3276. Vivod iz zapoya na domy_blPt

    Слушайте что расскажу. Попал я в переплёт конкретный. Брат пьёт без остановки. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, нормальные врачи нашлись — анонимный вывод из запоя без последствий. Приехали через час. В общем, вся инфа вот здесь — вывод из запоя на дому в екатеринбурге [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru[/url] Не тяните. Перешлите тому кому надо.

  3277. AbelItani

    Will be sharing this with a couple of people who care about the topic, and a stop at agatebrindle added more material worth passing along, the kind of site that is generous with quality content and does not make you jump through hoops to access it which is appreciated more than the team probably realises.

  3283. Stanleyrit

    However selective I am about new bookmarks this one made it past my filter, and a look at flaxbeech confirmed the bookmark was worth the slot, the precious slots in my permanent bookmark folder are difficult to earn and this site earned one without making me think twice about whether the slot was justified by the quality.

  3284. DaltonAduff

    Now adding this site to a small mental group of recommendations I keep ready for specific kinds of inquiries, and a stop at glybrow extended the recommendation readiness, content that I can confidently point friends and colleagues toward in specific contexts is content with real social utility and this site has that utility clearly.

  3285. BrentDok

    Just want to recognise that someone clearly cared about how this turned out, and a look at cricketcameo confirmed that care extends across the broader site, you can feel the difference between content shipped to hit a deadline and content released because the writer was actually proud of the result for once.

  3286. Jadenuteby

    Reading this on a phone at a coffee shop and finding it perfectly suited to that context, and a stop at tinyharbor continued the comfortable mobile experience, content that works across reading conditions without compromising on substance is increasingly important and this site has clearly thought about the whole reader experience here.

  3287. Seanvow

    Solid stuff, the kind of post that I will probably refer back to later this month when the topic comes up again, and a look at canyonclover only confirmed I should bookmark the site as a whole rather than just this single page for future reference and use across coming weeks.

  3288. BorisBal

    Now realising this site has been quietly doing good work for longer than I knew, and a look at baroncanyon suggested an archive worth exploring, sites with deep archives of consistent quality represent a different kind of resource than sites with viral hits and this one looks like the durable kind based on what I see.

  3289. Vivod iz zapoya na domy_dgMi

    Самарцы всем привет. Столкнулся с такой бедой. Брат пьёт без остановки. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, единственное что реально помогло — профессиональное выведение из запоя капельницей. Приехали через час. В общем, жмите чтобы не потерять — вывод из запоя цены [url=https://vyvod-iz-zapoya-na-domu-samara-vwx.ru]вывод из запоя цены[/url] Не тяните. Перешлите тому кому надо.

  3290. Leroydug

    Bookmark earned, calendar reminder set, share queued, all from one good post, and a look at rubymeadowcommercegallery did the same, when a single reading session triggers multiple downstream actions you know the content has actually moved me beyond the page and this site is moving me at that higher level reliably.

  3291. Kenagirl

    A piece that handled multiple complications without becoming confused, and a look at streamingstash continued that organisational clarity, holding multiple threads in a single piece without losing any of them is a sign of skilled writing and this site has clearly developed the editorial discipline to manage complexity without sacrificing readability throughout.

  3293. Vivod iz zapoya na domy_zzsl

    Слушайте что расскажу. Столкнулся с такой бедой. Муж просто пропадает. Дети не спят ночами. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — вывод из запоя дешево и сердито. Отошёл за полчаса. В общем, смотрите сами по ссылке — выведение из запоя цена [url=https://vyvod-iz-zapoya-na-domu-samara-yza.ru]https://vyvod-iz-zapoya-na-domu-samara-yza.ru[/url] Каждая минута дорога. Перешлите тому кому надо.

  3294. BuddyKen

    Quality writing that respects the reader’s intelligence without overloading them, and a quick look at ermineattic reflected that approach, a balanced thoughtful site that earns trust by being consistent rather than by shouting about how trustworthy it is which is the usual approach online sadly across most content categories.

  3297. MalcolmSax

    Will be passing this along to a few people who would benefit from the perspective shared here, and a stop at nyxsip only added to what I will be sharing, this kind of generous content deserves to circulate widely rather than getting buried in some search engine algorithm tweak that pushes it down the rankings.

  3300. KobeDably

    If patience for careful reading is rare these days finding sites that reward it is rarer still, and a stop at icicleislemerchantgallery extended that rare reward, the diminishing returns on shallow content reading have made me more selective about where to spend reading time and this site is meeting the higher selectivity bar consistently.

  3301. JadenSeage

    Quietly enthusiastic about this site after the past few hours of reading, and a stop at flaxbuckle extended that enthusiasm, the calibration of enthusiasm to evidence is something I try to maintain and this site has earned a calibrated quiet enthusiasm rather than the loud excitement that usually fades within a day or two of finding something.

  3302. Vivod iz zapoya na domy_eePt

    Слушайте что расскажу. Столкнулся с такой бедой. Человек уже четвёртые сутки в штопоре. Жена в слезах. В диспансер везти — учёт на всю жизнь. Короче, единственное что реально помогло — вывод из запоя цены адекватные. Приехали через час. В общем, жмите чтобы не потерять — капельница от запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru[/url] Каждая минута дорога. Перешлите тому кому надо.

  3303. EthanKax

    Coming to this with low expectations and being pleasantly surprised by the substance, and a stop at answerharbor continued exceeding expectations, the recalibration of expectations upward across multiple positive readings is one of the actual rewards of careful browsing and this site is providing that recalibration at a steady rate apparently.

  3304. SilasShire

    Reading this in a quiet coffee shop matched the calm energy of the writing, and a stop at cricketgourd extended that environmental match, content that has its own ambient quality which can match or clash with surroundings is content with a personality and this site has the kind of personality that suits calm reading.

  3305. PedroMop

    Honest reaction is that this is the kind of writing I would defend in a conversation about good blog content, and a look at elfincamel reinforced that, the rare site whose work I would actively recommend rather than just tolerate is the kind I want to support through return visits regularly.

  3306. Vivod iz zapoya na domy_jcki

    Самарцы всем привет. Жесть случилась полная. Человек уже пятые сутки в штопоре. Дети не спят ночами. Скорая не едет. Короче, нормальные врачи нашлись — вывод из запоя дешево и сердито. Приехали через час. В общем, сохраняйте на будущее — вывести из запоя срочно [url=https://vyvod-iz-zapoya-na-domu-samara-bcd.ru]https://vyvod-iz-zapoya-na-domu-samara-bcd.ru[/url] Не надейтесь на авось. Скиньте другу в беде.

  3307. Vivod iz zapoya na domy_dwMi

    Слушайте что расскажу. Попал я в переплёт конкретный. Брат пьёт без остановки. Жена в слезах. Скорая не едет. Короче, единственное что реально помогло — профессиональное выведение из запоя капельницей. Приехали через час. В общем, смотрите сами по ссылке — вывести из запоя цена [url=https://vyvod-iz-zapoya-na-domu-samara-vwx.ru]вывести из запоя цена[/url] Не надейтесь на авось. Скиньте другу в беде.

  3308. Riverniz

    A thoughtful piece that did not strain to be thoughtful, and a look at lyxbark continued that effortless quality, when thinking shows up in writing without the writer drawing attention to it you know you are reading something genuinely considered rather than something performing the appearance of consideration which is also common online.

  3309. Cassidyquevy

    Decided to write a short note to the author if there is contact info anywhere, and a stop at batikcitrine extended that intention, the urge to thank the writer directly is a strong signal of content quality and this site has triggered that urge in me today which is a fairly rare event for my reading.

  3310. HermanPathe

    Felt like the writer was speaking directly to someone with my level of curiosity, neither talking down nor showing off, and a stop at carbonantler kept that comfortable matching going, finding writing that meets you where you are rather than asking you to climb up or stoop down feels great every time it happens.

  3311. JulianGonry

    A piece that did not require external context to follow, and a look at snowcovemerchantgallery maintained the same self contained quality, content that stands alone without forcing readers to chase prerequisites is more accessible and this site has clearly thought about how each piece can serve a fresh visitor rather than only existing members.

  3312. Vivod iz zapoya na domy_muMn

    Ребята. Такая херня приключилась. Жена места не находит. Участковый только руками разводит. В итоге, единственные кто не побоялся приехать — анонимное выведение из запоя без учёта. Через пару часов человек задышал. В общем, сохраните чтобы не искать — вывод из запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-rfj.ru]вывод из запоя на дому цена[/url] Звоните пока не поздно. Кто в беде — тому пригодится.

  3313. Vivod iz zapoya na domy_semn

    Слушайте. Человек в завязке уже почти неделю. Жена в истерике. В диспансер тащить — клеймо на всю жизнь. Короче, единственные кто взялся и не прогадал — вывод из запоя на дому анонимно. Через 40 минут уже были. В общем, все контакты по ссылке — вывести из запоя цена [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru[/url] Звоните пока не поздно. Кто в беде — тому точно.

  3314. Nicolaslag

    Now realising the post has been quietly doing important work in my mind for the past hour, and a stop at uxupgrade extended that quiet processing, content that continues to do work after I close the tab is content with afterlife in the mind and this site is producing those long lived effects at a meaningful rate.

  3315. WilsonElory

    Honestly thank you to whoever wrote this because it scratched an itch I had not quite been able to articulate, and a stop at erminecobble kept that satisfying feeling going, the kind of writing that meets unspoken needs is special and this site clearly has writers who understand their readers more than most do today.

  3316. Vivod iz zapoya na domy_kcsl

    Самарцы привет. Попал я в переплёт конкретный. Брат пьёт без остановки. Соседи стучат в дверь. В диспансер везти — учёт на всю жизнь. Короче, нормальные врачи нашлись — вывод из запоя дешево и сердито. Приехали через час. В общем, смотрите сами по ссылке — вывод из запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-samara-yza.ru]https://vyvod-iz-zapoya-na-domu-samara-yza.ru[/url] Не тяните. Скиньте другу в беде.

  3317. Dwaynecrupt

    Регистрация в казино Вавада проста и открывает доступ к бонусам и турнирам. Инструменты ответственной игры позволяют задавать лимиты и контролировать бюджет. Мобильная версия полностью адаптирована и работает без задержек на любом устройстве. Регулярные турниры и еженедельный кэшбэк дают игрокам дополнительную выгоду. Актуальный вход открывает вавада.

  3318. Vivod iz zapoya na domy_dbMi

    Слушайте что расскажу. Попал я в переплёт конкретный. Близкий не выходит из запоя. Дети не спят ночами. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — профессиональное выведение из запоя капельницей. Приехали через час. В общем, там контакты и прайс — выведения из запоя на дому круглосуточно [url=https://vyvod-iz-zapoya-na-domu-samara-vwx.ru]выведения из запоя на дому круглосуточно[/url] Не тяните. Перешлите тому кому надо.

  3319. Jaimefuh

    Picked up something useful for a side project, and a look at ivoryridgemerchantgallery added another piece I will incorporate, content that connects to specific projects I am working on is content with practical utility and the practical utility of this site is showing up across multiple posts I have read in the last hour or so.

  3320. AriDuh

    Liked the way the post handled the final paragraph, no neat bow but no abrupt cutoff either, and a stop at flaxcargo continued that thoughtful ending pattern, endings are hard and most blog writers either over engineer them or skip them entirely and this site has clearly figured out a sustainable middle approach.

  3321. Vivod iz zapoya na domy_ijki

    Друзья ситуация жуткая. Попал я в переплёт конкретный. Человек уже пятые сутки в штопоре. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, единственное что реально помогло — вывод из запоя дешево и сердито. Приехали через час. В общем, вся инфа вот здесь — запой на дому [url=https://vyvod-iz-zapoya-na-domu-samara-bcd.ru]https://vyvod-iz-zapoya-na-domu-samara-bcd.ru[/url] Не надейтесь на авось. Скиньте другу в беде.

  3322. LionelVon

    Reading this prompted me to subscribe to my first newsletter in months, and a stop at carboncobble confirmed the subscribe was the right call, content that earns a newsletter signup is content that has cleared a higher trust bar than a casual visit and this site has clearly earned that level of commitment from me.

  3323. Wilburfrork

    Great work on keeping things readable, the post never drags or repeats itself which I really appreciate, and a stop at driveharbor added a bit more context that fit naturally with what was already said here, no need to read everything twice to get the point being made today.

  3324. Vivod iz zapoya na domy_bcPt

    Слушайте что расскажу. Попал я в переплёт конкретный. Брат пьёт без остановки. Соседи стучат в дверь. Платные клиники просят бешеные деньги. Короче, только это и спасло — анонимный вывод из запоя без последствий. Поставили систему. В общем, сохраняйте на будущее — нарколог на дом вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru]нарколог на дом вывод из запоя на дому[/url] Каждая минута дорога. Скиньте другу в беде.

  3325. Vivod iz zapoya na domy_tbMn

    Слушайте. Близкий человек в завязке. Родня разрывает телефон. Наркология платная — деньги выкачивают. В итоге, выручили только эти ребята — анонимное выведение из запоя без учёта. Поставили систему детокс. В общем, там и цены и контакты — вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-rfj.ru]вывод из запоя[/url] Звоните пока не поздно. Кто в беде — тому пригодится.

  3326. Eliplurn

    Worth flagging that the writing rewarded a second read more than I expected, and a look at solarorchardmerchantgallery produced the same second read benefit, content with hidden depths that emerge only on careful rereading is rare in the modern blog space and this site has clearly invested in that level of compositional density throughout.

  3327. Kentonmar

    Really appreciate this kind of writing, no shouting and no clickbait headlines just steady useful content, and a quick look at oxaboon kept that going, definitely a site I will be returning to whenever I need a sensible take on similar topics in the days ahead and also during slower work weeks.

  3328. Rufusglast

    Coming back to this one, definitely, and a quick visit to soontornado only made me more sure of that, the kind of writing that makes you want to set aside time later rather than rushing through it now while distracted by everything else competing for attention on the screen today across so many tabs.

  3329. JacksonNeism

    Reading this prompted me to send the link to two different people for two different reasons, and a stop at satinspindle provided ammunition for a third share, content that suits multiple audiences without being generic enough to be useless to any of them is genuinely valuable and this site has that multi audience quality clearly.

  3330. Vivod iz zapoya na domy_npMi

    Слушайте что расскажу. Столкнулся с такой бедой. Человек уже третьи сутки в штопоре. Жена в слезах. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — анонимный вывод из запоя без последствий. Приехали через час. В общем, там контакты и прайс — запой выезд на дом [url=https://vyvod-iz-zapoya-na-domu-samara-vwx.ru]запой выезд на дом[/url] Каждая минута дорога. Перешлите тому кому надо.

  3331. Vivod iz zapoya na domy_remn

    Слушайте. Человек в завязке уже почти неделю. Жена в истерике. Платная клиника просто грабит. В итоге, спасла только эта контора — вывод из запоя цены доступные. К утру человек пришёл в себя. В общем, подробности и расценки тут — поставить капельницу от запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru[/url] Каждый день без помощи — минус здоровье. Кто в беде — тому точно.

  3334. Vivod iz zapoya na domy_hrSn

    Самарцы привет. Столкнулся с такой бедой. Муж просто пропадает. Дети не спят ночами. Скорая не едет. Короче, единственное что реально помогло — срочный вывод из запоя круглосуточно. Отошёл за полчаса. В общем, вся инфа вот здесь — вывод из запоя цена [url=https://vyvod-iz-zapoya-na-domu-samara-stu.ru]вывод из запоя цена[/url] Каждая минута дорога. Перешлите тому кому надо.

  3337. StanleyFleri

    Honest take is that this was better than I expected when I clicked through, and a look at fawnimpala reinforced that, the bar for online content has dropped so much that finding something thoughtful and well constructed feels almost noteworthy now which says more about the average than about this site itself.

  3338. Vivod iz zapoya na domy_wyMn

    Слушайте. Близкий человек в завязке. Жена места не находит. Скорая не приедет на такой вызов. В итоге, врачи из этой конторы реально спасли — круглосуточный вывод из запоя на дом. Примчались за полчаса. В общем, сохраните чтобы не искать — вывод из запоя наркология [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-rfj.ru]вывод из запоя наркология[/url] Промедление убивает. Кому надо перешлите.

  3339. Vivod iz zapoya na domy_ckki

    Народ выручайте. Попал я в переплёт конкретный. Брат пьёт без остановки. Дети не спят ночами. Скорая не едет. Короче, единственное что реально помогло — вывести из запоя на дому качественно. Поставили систему. В общем, смотрите сами по ссылке — выведение из запоя на дому анонимно [url=https://vyvod-iz-zapoya-na-domu-samara-bcd.ru]https://vyvod-iz-zapoya-na-domu-samara-bcd.ru[/url] Каждая минута дорога. Перешлите тому кому надо.

  3340. Vivod iz zapoya na domy_dwsl

    Самарцы привет. Столкнулся с такой бедой. Человек уже четвёртые сутки в штопоре. Соседи стучат в дверь. Скорая не едет. Короче, только это и спасло — вывод из запоя дешево и сердито. Отошёл за полчаса. В общем, жмите чтобы не потерять — нарколог на дом вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-samara-yza.ru]https://vyvod-iz-zapoya-na-domu-samara-yza.ru[/url] Не надейтесь на авось. Перешлите тому кому надо.

  3341. GageElodo

    Now recognising that this site has earned a place in the small group of resources I treat as authoritative, and a stop at flaxdune confirmed that placement, the difference between resources I trust and resources I just consume is real and this site has clearly moved into the trusted category through consistent quality over time.

  3342. StuartapAks

    Thank you for not assuming the reader already knows everything, the explanations meet me where I am, and a look at valeharborcommercegallery did the same, that consideration is what makes a site feel welcoming rather than gatekeepy which is sadly the default mood across the modern web today for most subjects covered.

  3344. Vivod iz zapoya na domy_abPt

    Народ выручайте. Столкнулся с такой бедой. Близкий не выходит из запоя. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, только это и спасло — вывод из запоя недорого и качественно. Поставили систему. В общем, жмите чтобы не потерять — сколько стоит прокапаться от алкоголя цена [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru[/url] Не тяните. Скиньте другу в беде.

  3349. BrendanZEW

    Just dropping by to say thanks for the effort, it does not go unnoticed when a writer cares this much about the reader, and after I went through modernvertex I was certain this is one of the better corners of the internet for this particular kind of content which is genuinely refreshing.

  3350. Vivod iz zapoya na domy_iiMi

    Слушайте что расскажу. Столкнулся с такой бедой. Человек уже третьи сутки в штопоре. Дети не спят ночами. Скорая не едет. Короче, только это и спасло — вывод из запоя дешево и сердито. Отошёл за полчаса. В общем, жмите чтобы не потерять — вывести из запоя капельница на дому цена [url=https://vyvod-iz-zapoya-na-domu-samara-vwx.ru]вывести из запоя капельница на дому цена[/url] Каждая минута дорога. Перешлите тому кому надо.

  3351. TristanUnerb

    Solid stuff, the kind of post that I will probably refer back to later this month when the topic comes up again, and a look at visavoyage only confirmed I should bookmark the site as a whole rather than just this single page for future reference and use across coming weeks.

  3352. Vivod iz zapoya na domy_nyMn

    Екатеринбург. Сосед просто спивается на глазах. Жена места не находит. Наркология платная — деньги выкачивают. Короче говоря, выручили только эти ребята — вывод из запоя на дому с капельницей. Через пару часов человек задышал. В общем, сохраните чтобы не искать — нарколог на дом вывод [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-rfj.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-rfj.ru[/url] Промедление убивает. Кто в беде — тому пригодится.

  3353. Vivod iz zapoya na domy_kpst

    Народ. Муж пьёт беспробудно. Жена рыдает. Платная клиника дерёт три шкуры. В итоге, спасли только эти врачи — вывод из запоя на дому анонимно. Приехали быстро. В общем, жмите чтобы не забыть — капельница на дому от запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-gkd.ru]капельница на дому от запоя[/url] Не тяните время. Перешлите кому надо.

  3354. Vivod iz zapoya na domy_bsMr

    Приветствую народ. Случилась жесть. Соседи уже стучат в стену. Скорая отказывается выезжать на такие вызовы. В итоге, реально спасли эти врачи — анонимное выведение из запоя без учёта. К утру человек пришёл в себя. В общем, жмите чтобы сохранить — нарколог на дом вывод [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru[/url] Звоните сейчас. Может кому-то спасёт жизнь.

  3356. Vivod iz zapoya na domy_hzmn

    Слушайте. Близкий пьёт беспробудно. Родственники места себе не находят. Скорую вызывать бесполезно — всё равно не приедут. Короче, врачи реально вытащили — вывод из запоя цены доступные. Через 40 минут уже были. В общем, жмите чтобы не забыть — нарколог капельницу на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru[/url] Каждый день без помощи — минус здоровье. Скиньте кому пригодится.

  3357. Vivod iz zapoya na domy_eyki

    Друзья ситуация жуткая. Столкнулся с такой бедой. Человек уже пятые сутки в штопоре. Соседи стучат в дверь. Скорая не едет. Короче, нормальные врачи нашлись — вывести из запоя на дому качественно. Приехали через час. В общем, жмите чтобы не потерять — срочный вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-samara-bcd.ru]срочный вывод из запоя[/url] Не тяните. Скиньте другу в беде.

  3358. JuanPam

    Liked how the post handled an objection I was forming as I read, and a stop at flaxermine similarly anticipated where my thinking was going next, the rare writer who can predict reader concerns and address them in advance is doing something most online content fails to do despite that being basic editorial work.

  3359. Blakecen

    Now feeling confident enough in this site to use it as a reference point for evaluating others on the same topic, and a look at walnutcovemerchantgallery continued the comparison friendly quality, sites that serve as quality benchmarks for their topic are precious and this one has clearly become a benchmark for me on this particular subject area.

  3360. Vivod iz zapoya na domy_lasl

    Друзья ситуация. Столкнулся с такой бедой. Муж просто пропадает. Жена в слезах. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — вывести из запоя на дому качественно. Отошёл за полчаса. В общем, смотрите сами по ссылке — капельница от запоя телефон [url=https://vyvod-iz-zapoya-na-domu-samara-yza.ru]https://vyvod-iz-zapoya-na-domu-samara-yza.ru[/url] Каждая минута дорога. Скиньте другу в беде.

  3361. Vivod iz zapoya na domy_hsMn

    Ребята. Такая херня приключилась. Соседи уже звонят в полицию. Участковый только руками разводит. В итоге, врачи из этой конторы реально спасли — круглосуточный вывод из запоя на дом. Примчались за полчаса. В общем, жмите сейчас не пожалеете — вызов нарколога на дом капельница [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-rfj.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-rfj.ru[/url] Не ждите чуда. Кто в беде — тому пригодится.

  3362. Vivod iz zapoya na domy_lpPt

    Екатеринбург привет. Столкнулся с такой бедой. Человек уже четвёртые сутки в штопоре. Соседи стучат в дверь. Платные клиники просят бешеные деньги. Короче, только это и спасло — срочный вывод из запоя с капельницей. Приехали через час. В общем, смотрите сами по ссылке — вывод из запоя на дому в екатеринбурге [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru[/url] Не надейтесь на авось. Перешлите тому кому надо.

  3363. Vivod iz zapoya na domy_omPn

    Всем привет из Екб. Мой знакомый в запое четвёртые сутки. Родные не знают, за что хвататься. В бесплатную наркологию — табу. Короче говоря, спасла только эта служба — вывод из запоя на дому срочно. Укололи детокс. В общем, цены и телефон тут — вывод из запоя на дому екатеринбург [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-hjm.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-hjm.ru[/url] Каждая минута на вес золота. Вдруг пригодится.

  3364. Vivod iz zapoya na domy_shOn

    Всем здравствуйте. Ситуация аховая. Жена уже не знает куда бежать. В диспансер отвозить — стыдоба. Короче, действительно профессиональная бригада — круглосуточный вывод из запоя в Екатеринбурге. Вкапали систему сразу. В общем, жмите чтобы не забыть — вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-pcl.ru]вывод из запоя на дому[/url] Звоните прямо сейчас. Кому-то это может спасти жизнь.

  3365. Vivod iz zapoya na domy_avst

    Народ. Брат в штопоре. Дети боятся. Скорая отказывается приезжать. В итоге, единственные кто не побоялся взяться — срочное выведение из запоя с капельницей. Сняли интоксикацию за час. В общем, сохраните на будущее — вывод из запоя екатеринбург [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-gkd.ru]вывод из запоя екатеринбург[/url] Не тяните время. Перешлите кому надо.

  3366. Owenbot

    A piece that brought a sense of order to a topic I had been finding chaotic, and a look at ukurban continued that organising effect, content that imposes useful structure on messy subjects is doing genuine intellectual work and this site is providing that organisational function across multiple posts I have read recently here.

  3367. KurtGon

    Held my interest from the opening line through to the closing thought, and a stop at flintbunting did the same, content that earns sustained attention in an environment full of distractions is doing something right and this site is clearly doing several things right rather than just one or two which I really appreciate.

  3368. Vivod iz zapoya na domy_iiki

    Друзья ситуация жуткая. Жесть случилась полная. Человек уже пятые сутки в штопоре. Жена в слезах. Платные клиники просят бешеные деньги. Короче, единственное что реально помогло — профессиональное выведение из запоя капельницей. Приехали через час. В общем, там контакты и прайс — выведение из запоя на дому анонимно [url=https://vyvod-iz-zapoya-na-domu-samara-bcd.ru]https://vyvod-iz-zapoya-na-domu-samara-bcd.ru[/url] Не надейтесь на авось. Перешлите тому кому надо.

  3369. Keenanexeds

    Worth saying that the writing carries a particular kind of authority without making any explicit claims to it, and a stop at sailorvertex extended that earned authority feeling, sites that demonstrate expertise through the quality of their explanations rather than by stating credentials are sites I trust most and this site has it.

  3370. Vivod iz zapoya na domy_mimn

    Ребята в Екбе. Знакомый совсем ушёл в штопор. Родственники места себе не находят. Платная клиника просто грабит. В итоге, врачи реально вытащили — срочный вывод из запоя с выездом врача. Капельницу поставили сразу. В общем, подробности и расценки тут — вывод из запоя с выездом [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru]вывод из запоя с выездом[/url] Звоните пока не поздно. Кто в беде — тому точно.

  3371. Vivod iz zapoya na domy_cbMn

    Народ в Екбе. Сосед просто спивается на глазах. Родня разрывает телефон. Наркология платная — деньги выкачивают. В итоге, врачи из этой конторы реально спасли — вывод из запоя цены ниже чем в клиниках. Сняли ломку быстро. В общем, вся информация по ссылке — вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-rfj.ru]вывод из запоя на дому[/url] Звоните пока не поздно. Кто в беде — тому пригодится.

  3372. DaleRob

    Liked the balance between depth and brevity, never too shallow and never too long, and a stop at waveharborcommercegallery kept the same balance going across the rest of the site, this is one of the harder skills in writing and the team here clearly has it figured out very well indeed across every page.

  3373. RalphGib

    Came in for one specific question and got answers to three I had not even thought to ask, and a look at flaxgourd extended that bonus value pattern, the kind of resource that anticipates reader needs rather than just answering the literal question asked is the gold standard and this site reaches it.

  3374. Vivod iz zapoya na domy_bpsl

    Слушайте что расскажу. Попал я в переплёт конкретный. Близкий не выходит из запоя. Дети не спят ночами. Скорая не едет. Короче, нормальные врачи нашлись — вывод из запоя дешево и сердито. Поставили систему. В общем, смотрите сами по ссылке — вывод из запоя на дому самара цены [url=https://vyvod-iz-zapoya-na-domu-samara-yza.ru]https://vyvod-iz-zapoya-na-domu-samara-yza.ru[/url] Не тяните. Скиньте другу в беде.

  3375. Vivod iz zapoya na domy_tsPn

    Добрый день. Брат снова в штопоре. Жена места себе не находит. В бесплатную наркологию — табу. Короче говоря, единственные кто помог без нервотрёпки — профессиональный вывод из запоя недорого. Выехали быстро. В общем, вся инфа и контакты по ссылке — нарколог вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-hjm.ru]нарколог вывод из запоя[/url] Каждая минута на вес золота. Киньте ссылку тем, кто рядом с бедой.

  3376. Vivod iz zapoya na domy_ahOn

    Здарова, народ. Муж вообще потерял связь с реальностью. Дети всего боятся. В диспансер отвозить — стыдоба. Короче, действительно профессиональная бригада — круглосуточный вывод из запоя в Екатеринбурге. Приехали за 40 минут. В общем, контакты и цены здесь — капельница на дому от запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-pcl.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-pcl.ru[/url] Звоните прямо сейчас. Кому-то это может спасти жизнь.

  3378. Vivod iz zapoya na domy_scki

    Слушайте что расскажу. Жесть случилась полная. Муж просто пропадает. Дети не спят ночами. Скорая не едет. Короче, только это и спасло — срочный вывод из запоя круглосуточно. Отошёл за полчаса. В общем, вся инфа вот здесь — выведение из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-samara-bcd.ru]выведение из запоя на дому[/url] Каждая минута дорога. Скиньте другу в беде.

  3379. Vivod iz zapoya na domy_btst

    Ребята в Екбе. Случилась беда. Соседи стучат в стену. Платная клиника дерёт три шкуры. Короче, единственные кто не побоялся взяться — вывод из запоя цены приемлемые. Приехали быстро. В общем, все контакты по ссылке — прокапаться от алкоголя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-gkd.ru]прокапаться от алкоголя[/url] Не тяните время. Кто в беде — тому пригодится.

  3380. Vivod iz zapoya na domy_hyPt

    Народ выручайте. Попал я в переплёт конкретный. Близкий не выходит из запоя. Дети не спят ночами. Платные клиники просят бешеные деньги. Короче, только это и спасло — срочный вывод из запоя с капельницей. Поставили систему. В общем, там контакты и прайс — нарколог на дом вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru[/url] Не тяните. Перешлите тому кому надо.

  3382. Vivod iz zapoya na domy_zpMn

    Народ в Екбе. Такая херня приключилась. Родня разрывает телефон. Скорая не приедет на такой вызов. Короче говоря, врачи из этой конторы реально спасли — недорогой вывод из запоя без предоплаты. Примчались за полчаса. В общем, там и цены и контакты — капельница от запоя на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-rfj.ru]капельница от запоя на дому[/url] Не ждите чуда. Кому надо перешлите.

  3384. Vivod iz zapoya na domy_ajmn

    Екатеринбург. Близкий пьёт беспробудно. Дети плачут. Платная клиника просто грабит. В итоге, спасла только эта контора — вывод из запоя на дому анонимно. Сняли интоксикацию за час. В общем, сохраните себе на всякий — вывод из запоя анонимно недорого [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru[/url] Не откладывайте. Скиньте кому пригодится.

  3385. Vivod iz zapoya na domy_tyPn

    Здорово, народ. Мой знакомый в запое четвёртые сутки. Соседи уже стали коситься. В бесплатную наркологию — табу. Короче говоря, единственные кто помог без нервотрёпки — профессиональный вывод из запоя недорого. Выехали быстро. В общем, вся инфа и контакты по ссылке — капельница на дому от запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-hjm.ru]капельница на дому от запоя[/url] Каждая минута на вес золота. Киньте ссылку тем, кто рядом с бедой.

  3387. Yorkbouro

    Nice to see a post that does not try to overcomplicate the basics for the sake of looking smart, and once I looked at fudgebrindle the same direct tone was there too, which honestly makes a difference when you are short on time and want answers without long pointless intros.

  3388. Lanefah

    Honest take is that I will probably forget most of what I read online today but this post is one I will remember, and a stop at riderzenith kept that same memorable quality going, certain writing leaves a residue in the mind in a way most content simply does not manage.

  3389. Vivod iz zapoya na domy_kiOn

    Привет из Екатеринбурга. Муж вообще потерял связь с реальностью. Жена уже не знает куда бежать. В диспансер отвозить — стыдоба. Короче, действительно профессиональная бригада — вывод из запоя на дому анонимно. Человек ожил через пару часов. В общем, сохраните себе на всякий случай — нарколог вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-pcl.ru]нарколог вывод из запоя[/url] Не ждите чуда. Кому-то это может спасти жизнь.

  3390. Robertelacy

    Удобная система поиска делает полный справочник по почтовым отделениям России полезным инструментом для решения повседневных почтовых задач – https://pochtaops.ru/

  3391. Thomasjax

    Тимирязевский район считается одним из самых привлекательных для проживания благодаря сочетанию развитой инфраструктуры и большого количества зеленых территорий. Именно поэтому ЖК 26 ПаркВью вызывает высокий интерес у покупателей – https://26park.ru/

  3392. Greglaw

    Reading this as part of my evening winding down routine fit perfectly, and a stop at bisonfudge extended the wind down nicely, content that calms rather than agitates is what I want at the end of the day and this site provides that calming reading experience reliably which is increasingly rare across the modern web.

  3394. Vivod iz zapoya na domy_qyst

    Екатеринбург. Муж пьёт беспробудно. Жена рыдает. В диспансер везти — стыд на всю жизнь. В итоге, единственные кто не побоялся взяться — вывод из запоя цены приемлемые. Капельницу поставили сразу. В общем, все контакты по ссылке — вызов нарколога на дом капельница [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-gkd.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-gkd.ru[/url] Звоните прямо сейчас. Перешлите кому надо.

  3395. Vivod iz zapoya na domy_jhMn

    Ребята. Отец ушел в штопор четвертые сутки. Соседи уже звонят в полицию. Наркология платная — деньги выкачивают. Короче говоря, врачи из этой конторы реально спасли — недорогой вывод из запоя без предоплаты. Через пару часов человек задышал. В общем, сохраните чтобы не искать — вывод из запоя на дому екатеринбург круглосуточно [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-rfj.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-rfj.ru[/url] Не ждите чуда. Кто в беде — тому пригодится.

  3396. Vivod iz zapoya na domy_cmsl

    Слушайте что расскажу. Попал я в переплёт конкретный. Муж просто пропадает. Дети не спят ночами. Скорая не едет. Короче, только это и спасло — вывести из запоя на дому качественно. Отошёл за полчаса. В общем, жмите чтобы не потерять — вывод из запоя недорого [url=https://vyvod-iz-zapoya-na-domu-samara-yza.ru]вывод из запоя недорого[/url] Каждая минута дорога. Перешлите тому кому надо.

  3397. Stevenmet

    Веспер на Шаболовке привлекает внимание покупателей, которые ищут недвижимость в престижной части Москвы с хорошей транспортной доступностью и высоким уровнем комфорта, квартира в новостройке

  3398. Vivod iz zapoya na domy_bfPt

    Друзья ситуация. Попал я в переплёт конкретный. Близкий не выходит из запоя. Дети не спят ночами. В диспансер везти — учёт на всю жизнь. Короче, единственное что реально помогло — вывод из запоя недорого и качественно. Поставили систему. В общем, вся инфа вот здесь — вывод из запоя на дому екатеринбург круглосуточно [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru[/url] Каждая минута дорога. Скиньте другу в беде.

  3399. Vivod iz zapoya na domy_dxki

    Народ выручайте. Жесть случилась полная. Близкий не выходит из запоя. Жена в слезах. Платные клиники просят бешеные деньги. Короче, нормальные врачи нашлись — профессиональное выведение из запоя капельницей. Поставили систему. В общем, смотрите сами по ссылке — прерывание запоев на дому [url=https://vyvod-iz-zapoya-na-domu-samara-bcd.ru]https://vyvod-iz-zapoya-na-domu-samara-bcd.ru[/url] Каждая минута дорога. Перешлите тому кому надо.

  3400. Vivod iz zapoya na domy_odPn

    Здорово, народ. Кошмар полный. Соседи уже стали коситься. Скорая даже не рассматривает такие вызовы. Короче, реально крутые врачи попались — срочная капельница на дому от запоя. Укололи детокс. В общем, вся инфа и контакты по ссылке — капельница от запоя екатеринбург [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-hjm.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-hjm.ru[/url] Не тяните время. Киньте ссылку тем, кто рядом с бедой.

  3401. AlvinGop

    Speaking as someone who used to recommend blogs frequently and got out of the habit this site is rekindling that impulse, and a look at pyxedge extended the rekindling, the recovery of an old habit triggered by encountering work that justifies it is itself a small kind of pleasure and this site is providing that recovery experience.

  3407. alkoholizem_zqEl

    Preizkusil sem ze vse mogoce. Potem pa sem med brskanjem po spletu nasel nekaj, kar je spremenilo vse. Govorim o ambulantnem zdravljenju alkoholizma pri Dr Vorobjev centru. Veste, ni to le navada, ampak resna tezava. In ljudje se sramujejo prositi za pomoc. Zato vam zelim pokazati vse tehnicne podrobnosti in uradne informacije, ki so na voljo na tej povezavi: ambulantno zdravljenje alkoholizma [url=http://www.alkoholizma-zdravljenje.com]ambulantno zdravljenje alkoholizma[/url]. Tam boste nasli vse potrebne informacije.

    Zdaj zivim polno zivljenje brez alkohola. Vsak dan je bil izziv, ampak rezultat govori sam zase. Ce kogarkoli, ki ga imate radi ne ve, kam se obrniti – ne odlasajte. Nikoli ni prepozno za nov zacetek.

  3408. alkoholizem_qyot

    Pozdrav iz moje izkusnje. Upam, da bo komu koristilo. Bil sem na robu, iskreno povedano. Potem pa sem po priporocilu prijatelja nasel ambulantno zdravljenje alkoholizma pri metodi, ki resnicno deluje. Mislil sem, da je to se ena prevara. Ampak sem dal priloznost. In zdaj, ko gledam nazaj, lahko recem, da je bilo to resitev, ki sem jo iskal. Vec o tem in o celotnem postopku si lahko preberete neposredno na uradnem viru: ambulantno zdravljenje alkoholizma [url=https://www.alkoholizmazdravljenje.com]ambulantno zdravljenje alkoholizma[/url]. Ni lahko priznati, ampak se splaca.

    Ce kdo v vasi okolici potrebuje pomoc — ne odlasajte s to odlocitvijo. Nikoli ni prepozno za nov zacetek.

  3409. Vivod iz zapoya na domy_kqOn

    Доброго времени суток. Знакомый уже неделю в запое. Родственники на ушах стоят. Скорая не приедет — не тот случай. Короче, помогли только эти ребята — вывод из запоя на дому анонимно. Вкапали систему сразу. В общем, все данные по ссылке — нарколог на дом вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-pcl.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-pcl.ru[/url] Каждый час без помощи — это риск. Кому-то это может спасти жизнь.

  3410. Vivod iz zapoya na domy_oymn

    Ребята в Екбе. Человек в завязке уже почти неделю. Дети плачут. В диспансер тащить — клеймо на всю жизнь. В итоге, единственные кто взялся и не прогадал — вывод из запоя цены доступные. Сняли интоксикацию за час. В общем, сохраните себе на всякий — нарколог на дом вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru[/url] Звоните пока не поздно. Скиньте кому пригодится.

  3411. Vivod iz zapoya na domy_djMr

    Всем привет из Екатеринбурга. Близкий человек в запое. Жена в панике. Скорая отказывается выезжать на такие вызовы. Короче говоря, выручила только эта бригада — профессиональный вывод из запоя на дом. К утру человек пришёл в себя. В общем, жмите чтобы сохранить — вывод из запоя в екатеринбурге [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru[/url] Не откладывайте на завтра. Может кому-то спасёт жизнь.

  3412. Stevenmet

    Современные требования к жилью постоянно растут, и Vesper Шаболовка отвечает этим ожиданиям благодаря продуманной концепции и высокому качеству реализации, https://vesper-shabolovka.ru/

  3413. Vivod iz zapoya na domy_iest

    Слушайте. Случилась беда. Жена рыдает. Скорая отказывается приезжать. Короче, единственные кто не побоялся взяться — анонимный вывод из запоя без кодировки. Сняли интоксикацию за час. В общем, инфа и расценки тут — нарколог на дом вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-gkd.ru]нарколог на дом вывод из запоя[/url] Не тяните время. Кто в беде — тому пригодится.

  3414. ToddMurdy

    Generally I bookmark sparingly to avoid building up a bookmark graveyard but this one earned a permanent slot, and a stop at happyvoyager extended that permanence designation, the few sites I keep permanent bookmarks for are sites I expect to use repeatedly and this one has clearly cleared that expectation bar today.

  3415. Vivod iz zapoya na domy_xyPn

    Всем привет из Екб. Отец не приходит в себя. Соседи уже стали коситься. Скорая даже не рассматривает такие вызовы. Короче, единственные кто помог без нервотрёпки — вывод из запоя цены адекватные. Человек очнулся и задышал ровно. В общем, вся инфа и контакты по ссылке — вывод из запоя в екатеринбурге [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-hjm.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-hjm.ru[/url] Звоните не раздумывая. Киньте ссылку тем, кто рядом с бедой.

  3416. Vivod iz zapoya na domy_diMn

    Народ в Екбе. Родственник не выходит из пьянки. Соседи уже звонят в полицию. Участковый только руками разводит. В итоге, единственные кто не побоялся приехать — недорогой вывод из запоя без предоплаты. Сняли ломку быстро. В общем, сохраните чтобы не искать — врач на дом капельница от запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-rfj.ru]врач на дом капельница от запоя[/url] Промедление убивает. Кто в беде — тому пригодится.

  3418. Vivod iz zapoya na domy_jbPt

    Слушайте что расскажу. Попал я в переплёт конкретный. Брат пьёт без остановки. Жена в слезах. Платные клиники просят бешеные деньги. Короче, нормальные врачи нашлись — анонимный вывод из запоя без последствий. Поставили систему. В общем, сохраняйте на будущее — вывод из запоя цена [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru]вывод из запоя цена[/url] Не тяните. Скиньте другу в беде.

  3419. alkoholizem_vyot

    Zivjo, dolgo nisem pisal. Rad bi delil nekaj z vami. Bil sem na robu, iskreno povedano. Potem pa sem na spletu nasel zdravljenje alkoholizma pri Dr Vorobjevu. Nisem verjel, da bo delovalo. Ampak sem vseeno poskusil. In zdaj, po nekaj mesecih, lahko recem, da je bilo to najboljsa odlocitev. Vse uradne informacije in podrobnosti sem preveril na spletni strani, posodobljene podatke pa si lahko ogledate tukaj: zdravljenje alkoholizma [url=alkoholizmazdravljenje.com]zdravljenje alkoholizma[/url]. Ni lahko priznati, ampak se splaca.

    Ce kdo v vasi okolici potrebuje pomoc — ne odlasajte s to odlocitvijo. Nikoli ni prepozno za nov zacetek.

  3420. Vivod iz zapoya na domy_dyMr

    Здорова земляки. Муж в запое, не просыпается. Дети перепуганы. В диспансер тащить — позор на всю жизнь. В итоге, реально спасли эти врачи — срочный вывод из запоя с капельницей. Приехали в течение часа. В общем, вся информация по ссылке — выведение из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru[/url] Звоните сейчас. Отправьте тем кто в беде.

  3423. Vivod iz zapoya na domy_afOn

    Привет из Екатеринбурга. Ситуация аховая. Дети всего боятся. В диспансер отвозить — стыдоба. В итоге, единственные кто справился быстро — круглосуточный вывод из запоя в Екатеринбурге. Вкапали систему сразу. В общем, контакты и цены здесь — вывод из запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-pcl.ru]вывод из запоя на дому цена[/url] Не ждите чуда. Кому-то это может спасти жизнь.

  3424. JuanOpild

    Came in skeptical of the angle and left mostly persuaded, and a stop at agaveamber pushed me a bit further in the same direction, content that can move a critical reader by argument rather than rhetoric is rare and worth pointing out because it indicates real substance underneath the surface presentation here.

  3425. Vivod iz zapoya na domy_oxmn

    Народ. Человек в завязке уже почти неделю. Дети плачут. Платная клиника просто грабит. Короче, спасла только эта контора — вывод из запоя цены доступные. К утру человек пришёл в себя. В общем, все контакты по ссылке — капельница от запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru[/url] Не откладывайте. Кто в беде — тому точно.

  3426. DonovanMus

    Good post, the kind that respects the reader by getting to the point quickly without skipping the details that matter, and a short look at calicobanyan confirmed that approach is consistent across the site which is rare to find online these days, definitely a place I will return to soon.

  3427. Vivod iz zapoya na domy_daPn

    Всем привет из Екб. Кошмар полный. Жена места себе не находит. Скорая даже не рассматривает такие вызовы. Короче, единственные кто помог без нервотрёпки — вывод из запоя цены адекватные. Укололи детокс. В общем, сохраните в закладки обязательно — вывести из запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-hjm.ru]вывести из запоя[/url] Каждая минута на вес золота. Киньте ссылку тем, кто рядом с бедой.

  3428. Tonydrani

    Granted I am giving this site more credit than I usually give new finds, and a look at dailyneedsstore continued earning that credit, the calibration of how much trust to extend after limited exposure is something I do carefully and this site has earned more trust on shorter exposure than most due to consistent quality across.

  3429. Vivod iz zapoya na domy_aist

    Народ. Брат в штопоре. Соседи стучат в стену. Платная клиника дерёт три шкуры. Короче, спасли только эти врачи — вывод из запоя цены приемлемые. Сняли интоксикацию за час. В общем, жмите чтобы не забыть — капельница от запоя на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-gkd.ru]капельница от запоя на дому[/url] Звоните прямо сейчас. Кто в беде — тому пригодится.

  3430. Asherkeept

    Found this via a link from another piece I was reading and the click was worth it, and a stop at jaspermeadowcommercegallery extended the value across more material, the open web still rewards clicking through citations when the underlying writers care about each other work and this site clearly belongs to that network.

  3432. Vivod iz zapoya na domy_etMr

    Здорова земляки. Близкий человек в запое. Соседи уже стучат в стену. Скорая отказывается выезжать на такие вызовы. Короче говоря, единственные кто взялся без предоплат — недорогой вывод из запоя в Екатеринбурге. Сняли острую интоксикацию. В общем, контакты и расценки тут — прокапаться от алкоголя цены [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru[/url] Каждый час усугубляет состояние. Может кому-то спасёт жизнь.

  3433. alkoholizem_tcot

    Zivjo, dolgo nisem pisal. Rad bi delil nekaj z vami. Veste, alkohol je bil dolgo del mojega zivljenja. Potem pa sem po dolgem iskanju nasel ambulantno zdravljenje alkoholizma pri Dr Vorobjev centru. Bil sem poln dvomov. Ampak sem vseeno poskusil. In zdaj, po koncanem programu, lahko recem, da je bilo to resitev, ki sem jo iskal. Vec o tem in o celotnem postopku si lahko preberete neposredno na uradnem viru: alkoholizem [url=http://alkoholizmazdravljenje.com]alkoholizem[/url]. Odvisnost od alkohola ni sramota.

    Ce se vi ali kdo od vasih bliznjih sooca s tem — ne odlasajte s to odlocitvijo. Drzim pesti za vsakega, ki se bori

  3434. Vivod iz zapoya na domy_qyOn

    Доброго времени суток. Отец пьёт без просыпу. Жена уже не знает куда бежать. Скорая не приедет — не тот случай. В итоге, единственные кто справился быстро — круглосуточный вывод из запоя в Екатеринбурге. Человек ожил через пару часов. В общем, все данные по ссылке — прокапаться от алкоголя цены [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-pcl.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-pcl.ru[/url] Каждый час без помощи — это риск. Передайте тем, кто в беде.

  3436. Archlax

    Genuinely good work, the kind that holds up over multiple readings without losing its appeal, and a stop at bargainvertex kept that going, definitely a site I will be returning to and probably mentioning to others who work in or care about this particular area of interest today and in coming weeks.

  3437. Vivod iz zapoya na domy_qaPn

    Здорово, народ. Мой знакомый в запое четвёртые сутки. Дети ходят как в воду опущенные. Скорая даже не рассматривает такие вызовы. Короче, спасла только эта служба — срочная капельница на дому от запоя. Укололи детокс. В общем, вся инфа и контакты по ссылке — нарколог на дом вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-hjm.ru]нарколог на дом вывод из запоя на дому[/url] Не тяните время. Вдруг пригодится.

  3438. Vivod iz zapoya na domy_suPt

    Друзья ситуация. Жесть случилась полная. Брат пьёт без остановки. Жена в слезах. Платные клиники просят бешеные деньги. Короче, только это и спасло — срочный вывод из запоя с капельницей. Приехали через час. В общем, сохраняйте на будущее — вывод из запоя на дому круглосуточно [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-xtz.ru[/url] Не тяните. Скиньте другу в беде.

  3439. Edwardvaf

    ЖК Аурум Тайм от Град Девелопмент привлекает внимание покупателей благодаря современному облику и продуманной концепции жилого комплекса – Аурум Тайм от Град

  3440. Thomasjax

    Современные жилые комплексы должны предлагать больше, чем просто квартиры, и 26 ParkView является примером такого подхода к созданию комфортной городской среды: https://26park.ru/

  3442. Vivod iz zapoya na domy_krMr

    Здорова земляки. Брат пьёт без остановки. Жена в панике. В диспансер тащить — позор на всю жизнь. В итоге, выручила только эта бригада — профессиональный вывод из запоя на дом. Сняли острую интоксикацию. В общем, вся информация по ссылке — снятие интоксикации на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru[/url] Звоните сейчас. Может кому-то спасёт жизнь.

  3443. Vivod iz zapoya na domy_jomn

    Екатеринбург. Знакомый совсем ушёл в штопор. Жена в истерике. Скорую вызывать бесполезно — всё равно не приедут. Короче, спасла только эта контора — срочный вывод из запоя с выездом врача. Сняли интоксикацию за час. В общем, все контакты по ссылке — вывод из запоя капельница екатеринбург [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru[/url] Не откладывайте. Скиньте кому пригодится.

  3444. Vivod iz zapoya na domy_zmst

    Ребята в Екбе. Близкий человек в запое. Родственники не знают что делать. Скорая отказывается приезжать. В итоге, спасли только эти врачи — срочное выведение из запоя с капельницей. К утру человек в норме. В общем, сохраните на будущее — вывод из запоя екатеринбург [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-gkd.ru]вывод из запоя екатеринбург[/url] Звоните прямо сейчас. Кто в беде — тому пригодится.

  3446. KevinBIP

    Refreshing to read something where the words actually mean something instead of filling space, and a stop at erminecondor kept that going, the writing here trusts the reader to follow along without endless repetition or constant reminders of what was already said earlier in the post which I appreciate.

  3447. alkoholizem_xuot

    Pozdravljeni vsi skupaj. Moram povedati svojo zgodbo. Dolga leta sem se boril s to odvisnostjo. Potem pa sem po priporocilu prijatelja nasel zdravljenje alkoholizma pri Dr Vorobjev centru. Mislil sem, da je to se ena prevara. Ampak sem dal priloznost. In zdaj, ko gledam nazaj, lahko recem, da je bilo to najboljsa odlocitev. Sam sem preucil celoten program in vsi kljucni podatki so na voljo na tej povezavi: zdravljenje alkoholizma [url=https://www.alkoholizmazdravljenje.com]zdravljenje alkoholizma[/url]. Odvisnost od alkohola ni sramota.

    Ce se vi ali kdo od vasih bliznjih sooca s tem — ne odlasajte s to odlocitvijo. Drzim pesti za vsakega, ki se bori

  3448. alkoholizem_kvEl

    Dolga leta sem se boril sam. Potem pa sem po priporocilu nasel nekaj, kar je bilo prelomnica. Govorim o odvajanju od alkohola pri metodi, ki resnicno deluje. Veste, alkoholizem je bolezen. In veliko je slabih informacij. Zato priporocam, da preverite celoten postopek na spletni strani, ki so na voljo na tej povezavi: Dr Vorobjev [url=http://alkoholizma-zdravljenje.com]Dr Vorobjev[/url]. Tam boste nasli vse potrebne informacije.

    Zdaj zivim polno zivljenje brez alkohola. Pot je bila naporna, ampak vredno je bilo vsakega truda. Ce vi ali kdo od vasih bliznjih ne ve, kam se obrniti – resnicno priporocam. Nikoli ni prepozno za nov zacetek.

  3450. Vivod iz zapoya na domy_eeOn

    Привет из Екатеринбурга. Знакомый уже неделю в запое. Дети всего боятся. Скорая не приедет — не тот случай. В итоге, действительно профессиональная бригада — круглосуточный вывод из запоя в Екатеринбурге. Сняли ломку и абстиненцию. В общем, все данные по ссылке — сколько стоит прокапаться от алкоголя цена [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-pcl.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-pcl.ru[/url] Каждый час без помощи — это риск. Кому-то это может спасти жизнь.

  3451. Vivod iz zapoya na domy_zzPn

    Добрый день. Отец не приходит в себя. Родные не знают, за что хвататься. Скорая даже не рассматривает такие вызовы. Короче говоря, спасла только эта служба — вывод из запоя на дому срочно. Укололи детокс. В общем, сохраните в закладки обязательно — вывод из запоя екатеринбург [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-hjm.ru]вывод из запоя екатеринбург[/url] Каждая минута на вес золота. Вдруг пригодится.

  3452. alkoholizem_xvea

    Pozdravljeni, dragi moji. Danes bi rad spregovoril o necem pomembnem. Vsak dan je bil enak mucenje. Potem pa sem od prijatelja izvedel za to moznost. Govorim o odvajanju od alkohola pri strokovnjakih, ki res znajo pomagati. Mislil sem, da mi nic ne more pomagati. Ampak sem se odlocil за ta korak in zivljenje se je obrnilo na bolje. Vse uradne informacije in podrobnosti sem preveril na spletni strani, posodobljene podatke pa si lahko ogledate tukaj: Dr Vorobjev [url=https://www.odvajanje-od-alkoho.com]Dr Vorobjev[/url] Odvisnost od alkohola ni znak sibkosti.

    Ce vas prijatelj potrebuje pomoc — to je lahko odlocilni korak. Srecno na vasi poti!

  3453. Robertelacy

    Полный справочник по почтовым отделениям России объединяет сведения о работе отделений связи, почтовых индексах и адресах по всей территории страны: https://pochtaops.ru/

  3455. Jeremiahdup

    Quietly the writers approach to the topic differs from the dominant takes I have been encountering, and a stop at chimneycargo extended that distinctive approach, content that maintains a different perspective without explicitly arguing against the dominant ones is content with confident editorial identity and this site has that confidence throughout pieces.

  3456. Vivod iz zapoya na domy_uoMr

    Приветствую народ. Муж в запое, не просыпается. Родственники места себе не находят. В диспансер тащить — позор на всю жизнь. В итоге, реально спасли эти врачи — срочный вывод из запоя с капельницей. Поставили капельницу сразу. В общем, контакты и расценки тут — капельница от запоя недорого [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru[/url] Не откладывайте на завтра. Отправьте тем кто в беде.

  3457. FreddieRer

    Профессиональная школа английского для детей YES Center приглашает учеников от дошкольников до подростков. Игровые методики, опытные преподаватели и небольшие группы создают идеальные условия для обучения. Ребёнок заговорит уверенно и без страха ошибиться.

  3458. HarlanNex

    Came in skeptical of the angle and left mostly persuaded, and a stop at talentnexus pushed me a bit further in the same direction, content that can move a critical reader by argument rather than rhetoric is rare and worth pointing out because it indicates real substance underneath the surface presentation here.

  3459. BennieAdose

    Reading this prompted a brief but useful conversation with a colleague who happened to walk by, and a stop at eskimoarbor extended that conversational seed, content that becomes a starting point for in person discussion rather than ending in solitary reading is content with social generative energy and this site has plenty of it apparently.

  3460. Vivod iz zapoya na domy_mgst

    Слушайте. Отец не просыхает уже пятый день. Соседи стучат в стену. Платная клиника дерёт три шкуры. Короче, реально помогла эта бригада — вывод из запоя на дому анонимно. К утру человек в норме. В общем, все контакты по ссылке — вывод из запоя цены [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-gkd.ru]вывод из запоя цены[/url] Не тяните время. Кто в беде — тому пригодится.

  3461. Edwardvaf

    Благодаря продуманной концепции Aurum Time становится привлекательным вариантом как для собственного проживания, так и для долгосрочных инвестиций в недвижимость: жк аурум тайм

  3462. alkoholizem_daot

    Pozdrav iz moje izkusnje. Rad bi delil nekaj z vami. Bil sem na robu, iskreno povedano. Potem pa sem po priporocilu prijatelja nasel zdravljenje alkoholizma pri Dr Vorobjevu. Bil sem poln dvomov. Ampak sem vseeno poskusil. In zdaj, ko gledam nazaj, lahko recem, da je bilo to resitev, ki sem jo iskal. Sam sem preucil celoten program in vsi kljucni podatki so na voljo na tej povezavi: ambulantno zdravljenje alkoholizma [url=http://www.alkoholizmazdravljenje.com]ambulantno zdravljenje alkoholizma[/url]. Ni lahko priznati, ampak se splaca.

    Ce se vi ali kdo od vasih bliznjih sooca s tem — resnicno priporocam, da preberete. Drzim pesti za vsakega, ki se bori

  3463. alkoholizem_erEl

    Dolga leta sem se boril sam. Potem pa sem med brskanjem po spletu nasel nekaj, kar je spremenilo vse. Govorim o ambulantnem zdravljenju alkoholizma pri metodi, ki resnicno deluje. Veste, odvisnost od alkohola je zahrbtna. In veliko je slabih informacij. Zato priporocam, da preverite celoten postopek na spletni strani, ki so na voljo na tej povezavi: alkoholizem [url=http://alkoholizma-zdravljenje.com]alkoholizem[/url]. Tam boste nasli vse potrebne informacije.

    Meni je ta pristop pomagal. Vsak dan je bil izziv, ampak rezultat govori sam zase. Ce vi ali kdo od vasih bliznjih se sooca s to tezavo – resnicno priporocam. Nikoli ni prepozno za nov zacetek.

  3467. Vivod iz zapoya na domy_ijOn

    Здарова, народ. Отец пьёт без просыпу. Соседи грозятся вызвать полицию. В диспансер отвозить — стыдоба. В итоге, помогли только эти ребята — круглосуточный вывод из запоя в Екатеринбурге. Вкапали систему сразу. В общем, сохраните себе на всякий случай — капельница от запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-pcl.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-pcl.ru[/url] Не ждите чуда. Кому-то это может спасти жизнь.

  3468. Williamhor

    каратэ Рукопашный бой для взрослых позволяет выплеснуть накопленное напряжение после трудового дня. Тренировка становится отличной эмоциональной разрядкой для психики.

  3469. Vivod iz zapoya na domy_glPn

    Здорово, народ. Кошмар полный. Соседи уже стали коситься. В бесплатную наркологию — табу. Короче говоря, спасла только эта служба — вывод из запоя цены адекватные. Выехали быстро. В общем, вся инфа и контакты по ссылке — нарколог на дом вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-hjm.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-hjm.ru[/url] Каждая минута на вес золота. Вдруг пригодится.

  3470. alkoholizem_fiea

    Dober dan vsem, ki berete. Danes bi rad spregovoril o necem pomembnem. Bil sem ujetnik odvisnosti. Potem pa sem na spletu naletel na resitev. Govorim o ambulantnem zdravljenju alkoholizma pri Dr Vorobjevu. Mislil sem, da mi nic ne more pomagati. Ampak sem vseeno poskusil in zdaj sem clovek na novo rojen. Sam sem preucil celoten program in vsi kljucni podatki so na voljo na tej povezavi: odvajanje od alkohola [url=https://odvajanje-od-alkoho.com]odvajanje od alkohola[/url] Ni sramota prositi za pomoc.

    Ce vi sami potrebuje pomoc — prosim, ne odlasajte. Srecno na vasi poti!

  3471. Guyrag

    Now adding a small note in my reading log that this site is one to watch, and a look at eskimobadge reinforced the watch status, the few sites I track deliberately rather than encounter accidentally are sites I expect ongoing returns from and this one has cleared the bar for that elevated tracking based on what I read.

  3473. alkoholizem_xyot

    Zivjo, dolgo nisem pisal. Upam, da bo komu koristilo. Veste, alkohol je bil dolgo del mojega zivljenja. Potem pa sem na spletu nasel odvajanje od alkohola pri Dr Vorobjev centru. Bil sem poln dvomov. Ampak sem vseeno poskusil. In zdaj, ko gledam nazaj, lahko recem, da je bilo to najboljsa odlocitev. Vse uradne informacije in podrobnosti sem preveril na spletni strani, posodobljene podatke pa si lahko ogledate tukaj: zdravljenje alkoholizma [url=https://alkoholizmazdravljenje.com]zdravljenje alkoholizma[/url]. Ni lahko priznati, ampak se splaca.

    Ce iscete resitev za to tezavo — ne odlasajte s to odlocitvijo. Nikoli ni prepozno za nov zacetek.

  3474. JuliusAlobE

    Bookmark folder reorganised slightly to make this site easier to find, and a look at bloomhavenhub earned the same accessibility upgrade, the small organisational moves I make for sites I expect to return to often are themselves a signal of how much I trust them and this site triggered those moves naturally.

  3477. RobertSmalt

    финансовый эксперт Анализ рынка «финансов и кредитов» показывает, что дисциплинированные заемщики всегда имеют лучшие условия от банков. Работайте над своим кредитным рейтингом, чтобы получать самые низкие процентные ставки.

  3478. Vivod iz zapoya na domy_pcOn

    Привет из Екатеринбурга. Отец пьёт без просыпу. Родственники на ушах стоят. Скорая не приедет — не тот случай. В итоге, единственные кто справился быстро — вывод из запоя на дому анонимно. Сняли ломку и абстиненцию. В общем, жмите чтобы не забыть — вывод из запоя цена [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-pcl.ru]вывод из запоя цена[/url] Каждый час без помощи — это риск. Кому-то это может спасти жизнь.

  3482. alkoholizem_uaea

    Pozdravljeni, dragi moji. Rad bi delil svojo zgodbo. Alkohol je dolgo casa vodil moje zivljenje. Potem pa sem po dolgem iskanju koncno nasel pravo pot. Govorim o odvajanju od alkohola pri strokovnjakih, ki res znajo pomagati. Sprva nisem verjel. Ampak sem se odlocil за ta korak in koncno sem spet jaz. Vse uradne informacije in podrobnosti sem preveril na spletni strani, posodobljene podatke pa si lahko ogledate tukaj: Dr Vorobjev [url=https://www.odvajanje-od-alkoho.com]Dr Vorobjev[/url] Ni sramota prositi za pomoc.

    Ce vi sami se bori z alkoholom — vredno je poskusiti. Verjamem, da se da!

  3483. Vivod iz zapoya na domy_rpmn

    Здарова, народ. Близкий человек не вылезает из запоя. Соседи уже начали звонить в участок. В диспансер сдавать — ужас. Итог, только эти врачи смогли помочь — срочное выведение из запоя капельницей. К вечеру человек пришёл в сознание. В общем, вся информация по ссылке — капельница от запоя недорого [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-vqx.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-vqx.ru[/url] Не медлите. Вдруг это спасёт кого-то.

  3484. RobertoDoday

    земельные участки в мо Покупка участка под ИЖС требует внимательного изучения инженерных коммуникаций на месте. Наши эксперты помогут оценить все преимущества и риски каждого конкретного предложения.

  3485. alkoholizem_qqot

    Zivjo, dolgo nisem pisal. Rad bi delil nekaj z vami. Dolga leta sem se boril s to odvisnostjo. Potem pa sem po dolgem iskanju nasel zdravljenje alkoholizma pri Dr Vorobjev centru. Mislil sem, da je to se ena prevara. Ampak sem dal priloznost. In zdaj, po nekaj mesecih, lahko recem, da je bilo to najboljsa odlocitev. Sam sem preucil celoten program in vsi kljucni podatki so na voljo na tej povezavi: ambulantno zdravljenje alkoholizma [url=www.alkoholizmazdravljenje.com]ambulantno zdravljenje alkoholizma[/url]. Alkoholizem is bolezen, ne slabost.

    Ce se vi ali kdo od vasih bliznjih sooca s tem — ne odlasajte s to odlocitvijo. Nikoli ni prepozno za nov zacetek.

  3486. alkoholizem_hkEl

    Dolga leta sem se boril sam. Potem pa sem po nakljucju nasel nekaj, kar je spremenilo vse. Govorim o odvajanju od alkohola pri metodi, ki resnicno deluje. Veste, ni to le navada, ampak resna tezava. In ljudje se sramujejo prositi za pomoc. Zato vam zelim pokazati vse tehnicne podrobnosti in uradne informacije, ki so na voljo na tej povezavi: odvisnost od alkohol [url=http://alkoholizma-zdravljenje.com]odvisnost od alkohol[/url]. Tam boste nasli vse potrebne informacije.

    Po dolgih letih sem koncno nasel resitev. Pot je bila naporna, ampak rezultat govori sam zase. Ce nekdo v vasi okolici ne ve, kam se obrniti – resnicno priporocam. Drzim pesti za vsakega, ki se bori

  3487. 888starz_dbSi

    [url=https://888stars-egy.com]موقع مراهنات 888[/url] هي منصة مراهنات عبر الإنترنت تقدم ألعاب كازينو وخيارات رهان متنوعة للمستخدمين العرب.
    تعرف 888starz بكونها وجهة مفضلة لعشاق الألعاب الإلكترونية.

    القسم الثاني:
    تضم 888starz مكتبة ألعاب متنوعة تشمل السلاسل الكلاسيكية والجديدة.

    القسم الثالث:
    توفر 888starz قنوات دعم سريعة تساعد في حل المشكلات بكفاءة.

    القسم الرابع:
    تستضيف المنصة حملات ومكافآت دورية لتحفيز اللاعبين على المشاركة.

  3488. Vivod iz zapoya na domy_kxst

    Ребята в Екбе. Случилась беда. Дети боятся. В диспансер везти — стыд на всю жизнь. В итоге, реально помогла эта бригада — вывод из запоя на дому анонимно. К утру человек в норме. В общем, сохраните на будущее — вывод из запоя в екатеринбурге [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-gkd.ru]вывод из запоя в екатеринбурге[/url] Звоните прямо сейчас. Кто в беде — тому пригодится.

  3489. Vivod iz zapoya na domy_orMr

    Здорова земляки. Отец не выходит из штопора уже третьи сутки. Родственники места себе не находят. Скорая отказывается выезжать на такие вызовы. Короче говоря, единственные кто взялся без предоплат — вывод из запоя цены доступные. Приехали в течение часа. В общем, вся информация по ссылке — выведение из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru[/url] Каждый час усугубляет состояние. Может кому-то спасёт жизнь.

  3490. 888starz_efOr

    [url=https://888starzs6.com]stars 88[/url] هو موقع للمراهنات والألعاب الإلكترونية يقدم خدمات تسجيل الدخول والدعم بلغات متعددة.
    تُعد 888starz واحدة من أشهر منصات المراهنات والترفيه عبر الإنترنت.

    القسم الثاني:
    توفر 888starz ألعاب سلوتس وبث مباشر ومراهنات على المنافسات الرياضية.

    القسم الثالث:
    توفر العروض بفرص إضافية للعب وتجربة ألعاب متعددة دون تكلفة فورية كبيرة.

    القسم الرابع:
    تستخدم المنصة تقنيات تشفير وحماية متقدمة للحفاظ على سرية المعاملات.

  3492. 888starz_dcmi

    [url=https://888starzs8.com]88starz[/url]
    تُظهر آراء المستخدمين جوانب التميز والفرص التحسينية في تجربة 888starz.

  3493. 888starz_ayon

    На 888starz реализованы приветственные бонусы, периодические акции и кэшбэк для тех, кто играет регулярно.
    888starz betting [url=https://888starz-uzb4.com]888starz betting[/url].

  3494. 888starz_rqPr

    Открытие счета на 888starz проходит оперативно, без длительных верификаций при малых суммах.
    888starz зеркало [url=https://888starz-uzb6.com]https://888starz-uzb6.com[/url]

  3495. 888starz_cwPn

    جرب الحظ الآن على [url=https://888starsegypt.com]موقع مراهنات 888[/url] للفوز بجوائز مثيرة ومباشرة.
    تتسم واجهة 888starz بالبساطة وسهولة التصفح للمستخدمين.

    الفقرة الثانية:
    الخدمات تشمل ألعاب الكازينو والرياضات الافتراضية والعروض الترويجية.

  3496. 888starz_vsor

    [url=https://888starzs7.com]ازاي اسحب فلوس من 888starz[/url]
    تقدم 888starz تجربة شاملة للمستخدمين الباحثين عن الترفيه والمراهنات وألعاب الكازينو.

    القسم الثاني:
    تهتم 888starz بتحديث محتواها لضمان تجربة حديثة ومتنوعة للمستخدمين.

    القسم الثالث:
    تعتمد سياسة مكافآت مرنة تجذب اللاعبين وتكافئ نشاطهم على المنصة.

    القسم الرابع:
    تدعم 888starz وسائل إيداع وسحب متنوعة بما يشمل بطاقات الدفع الإلكتروني والمحافظ الرقمية وخيارات محلية.

  3497. 888starz_gdei

    В каталоге платформы представлены классические и современные слоты, а также настольные игры и трансляции с реальными дилерами.
    888starz casino login [url=888-uz10.com]https://888-uz10.com[/url]

  3498. 888starz_vipt

    Круглосуточная поддержка 888starz обеспечивает помощь пользователям по всем возникающим вопросам.

    Контактные каналы включают чат, электронную почту и раздел FAQ с подробными ответами.
    888bet skachat [url=888-uz1.com/apk]https://888-uz1.com/apk/[/url]

  3500. 888starz_xsKl

    Ассортимент игр на 888starz включает классические слоты, современные видеослоты и живые игры с дилерами.

    starz 888 casino [url=https://888-uz2.com/]https://888-uz2.com[/url]

  3501. Vivod iz zapoya na domy_pjmn

    Екатеринбург. Знакомый совсем ушёл в штопор. Соседи уже стучат в стену. В диспансер тащить — клеймо на всю жизнь. Короче, врачи реально вытащили — срочный вывод из запоя с выездом врача. Через 40 минут уже были. В общем, подробности и расценки тут — вывод из запоя анонимно недорого [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-bqm.ru[/url] Звоните пока не поздно. Скиньте кому пригодится.

  3502. Vivod iz zapoya na domy_hcmn

    Всем здравствуйте. Близкий человек не вылезает из запоя. Соседи уже начали звонить в участок. В диспансер сдавать — ужас. В общем, только эти врачи смогли помочь — срочное выведение из запоя капельницей. К вечеру человек пришёл в сознание. В общем, контакты и стоимость тут — вывод из запоя на дому круглосуточно [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-vqx.ru]вывод из запоя на дому круглосуточно[/url] Промедление может стоить здоровья. Вдруг это спасёт кого-то.

  3503. JavierHycle

    Started forming counter examples to test the claims and the post handled most of them implicitly, and a look at motovoyager continued that anticipatory style, writers who think two steps ahead of the critical reader save themselves from a lot of follow up work and this writer has clearly internalised that habit consistently.

  3504. Pingback: minoxidil women’s performance

  3505. alkoholizem_ygot

    Pozdravljeni vsi skupaj. Rad bi delil nekaj z vami. Veste, alkohol je bil dolgo del mojega zivljenja. Potem pa sem po dolgem iskanju nasel odvajanje od alkohola pri Dr Vorobjev centru. Bil sem poln dvomov. Ampak sem se odlocil za ta korak. In zdaj, ko gledam nazaj, lahko recem, da je bilo to resitev, ki sem jo iskal. Vec o tem in o celotnem postopku si lahko preberete neposredno na uradnem viru: alkoholizem [url=https://alkoholizmazdravljenje.com]alkoholizem[/url]. Odvisnost od alkohola ni sramota.

    Ce kdo v vasi okolici potrebuje pomoc — vzemite si cas in raziscite. Drzim pesti za vsakega, ki se bori

  3506. alkoholizem_hiea

    Zivjo vsem skupaj. Moram povedati nekaj iz prve roke. Bil sem ujetnik odvisnosti. Potem pa sem po dolgem iskanju koncno nasel pravo pot. Govorim o zdravljenju alkoholizma pri Dr Vorobjevu. Sprva nisem verjel. Ampak sem dal tej metodi priloznost in koncno sem spet jaz. Vec o tem in o celotnem postopku si lahko preberete neposredno na uradnem viru: alkoholizem [url=https://odvajanje-od-alkoho.com]alkoholizem[/url] Odvisnost od alkohola ni znak sibkosti.

    Ce kdo od druzinskih clanov ne vidi izhoda — vredno je poskusiti. Verjamem, da se da!

  3507. Vivod iz zapoya na domy_giSi

    Доброго времени. Брат совсем потерял человеческий облик. Дети напуганы до смерти. Скорая не реагирует на пьянку. Короче, профессиональные врачи с горячими руками — помощь нарколога на дому быстро. Врач осмотрел и начал детокс. В общем, цены и телефон тут — вывод из запоя круглосуточно [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru[/url] Не откладывайте. Киньте ссылку нуждающимся.

  3509. RobertSew

    все санкции РФ Следите за тем, как развивается санкционная повестка, с помощью наших графиков. Мы предоставляем только проверенную информацию из первых рук.

  3510. RobertoDoday

    земля под дачу Земельные участки в Подмосковье сегодня — это отличный выбор для тех, кто ценит экологию и близость к столице. Ознакомьтесь с актуальными лотами в различных направлениях региона.

  3511. Vivod iz zapoya na domy_usmn

    Доброго дня. Брат совсем потерял себя. Родственники не спят ночами. Скорая реагирует только на угрозу жизни. В общем, единственные кто приехал без лишних вопросов — срочное выведение из запоя капельницей. К вечеру человек пришёл в сознание. В общем, вся информация по ссылке — капельница от запоя недорого [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-vqx.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-vqx.ru[/url] Не медлите. Вдруг это спасёт кого-то.

  3513. Vivod iz zapoya na domy_jiMr

    Приветствую народ. Случилась жесть. Жена в панике. Платная наркология запрашивает бешеные деньги. Короче говоря, выручила только эта бригада — недорогой вывод из запоя в Екатеринбурге. Поставили капельницу сразу. В общем, не потеряйте вкладку — капельница от запоя на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-nws.ru]капельница от запоя на дому[/url] Каждый час усугубляет состояние. Отправьте тем кто в беде.

  3514. WyattSwoni

    The way the post stayed on topic throughout without going on tangents was really refreshing, and a look at primepropertygo kept that focused approach going, discipline like this in writing is rare and worth recognising because most writers cannot resist wandering off into related subjects that dilute their main point and confuse readers along the way.

  3515. Vivod iz zapoya na domy_wkSi

    Всем салют. Муж пьёт без остановки. Жена плачет. Скорая не реагирует на пьянку. Короче, единственные кто приехал без предоплаты — вывод из запоя на дому срочный. Сняли ломку и нормализовали давление. В общем, все контакты по ссылке — поставить капельницу от запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru[/url] Промедление может стоить жизни. Может, кому-то она спасёт близкого.

  3516. alkoholizem_hyea

    Pozdravljeni, dragi moji. Rad bi delil svojo zgodbo. Vsak dan je bil enak mucenje. Potem pa sem od prijatelja izvedel za to moznost. Govorim o odvajanju od alkohola pri strokovnjakih, ki res znajo pomagati. Bil sem preprican, da je zame prepozno. Ampak sem se odlocil за ta korak in koncno sem spet jaz. Vec o tem in o celotnem postopku si lahko preberete neposredno na uradnem viru: zdravljenje alkoholizma [url=http://www.odvajanje-od-alkoho.com]zdravljenje alkoholizma[/url] Ni sramota prositi za pomoc.

    Ce vas partner se bori z alkoholom — vredno je poskusiti. Srecno na vasi poti!

  3517. alkoholizem_dqEl

    Preizkusil sem ze vse mogoce. Potem pa sem po nakljucju nasel nekaj, kar je spremenilo vse. Govorim o zdravljenju alkoholizma pri Dr Vorobjevu. Veste, alkoholizem je bolezen. In veliko je slabih informacij. Zato svetujem, da si vzamete cas in preberete posodobljene podatke, ki so na voljo na tej povezavi: odvajanje od alkohola [url=https://www.alkoholizma-zdravljenje.com]odvajanje od alkohola[/url]. Na tej povezavi so odgovori na vsa vprasanja.

    Po dolgih letih sem koncno nasel resitev. Pot je bila naporna, ampak zdaj sem ponosen nase. Ce vi ali kdo od vasih bliznjih potrebuje pomoc – ne odlasajte. Drzim pesti za vsakega, ki se bori

  3518. alkoholizem_zzot

    Pozdrav iz moje izkusnje. Moram povedati svojo zgodbo. Veste, alkohol je bil dolgo del mojega zivljenja. Potem pa sem po priporocilu prijatelja nasel odvajanje od alkohola pri metodi, ki resnicno deluje. Mislil sem, da je to se ena prevara. Ampak sem se odlocil za ta korak. In zdaj, po nekaj mesecih, lahko recem, da je bilo to prelomnica v mojem zivljenju. Vec o tem in o celotnem postopku si lahko preberete neposredno na uradnem viru: odvisnost od alkohol [url=https://alkoholizmazdravljenje.com]odvisnost od alkohol[/url]. Odvisnost od alkohola ni sramota.

    Ce kdo v vasi okolici potrebuje pomoc — vzemite si cas in raziscite. Nikoli ni prepozno za nov zacetek.

  3519. Vivod iz zapoya na domy_smmn

    Всем здравствуйте. Беда пришла. Соседи уже начали звонить в участок. В диспансер сдавать — ужас. Итог, только эти врачи смогли помочь — анонимный вывод из запоя на дому. К вечеру человек пришёл в сознание. В общем, вся информация по ссылке — нарколог на дом вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-vqx.ru]нарколог на дом вывод из запоя[/url] Звоните немедленно. Вдруг это спасёт кого-то.

  3520. RobertoDoday

    участок под бизнес Красивый участок у воды подарит вам незабываемые моменты отдыха на свежем воздухе. Выбирайте землю рядом с водоемами, подходящими для рыбалки или купания.

  3527. Vivod iz zapoya na domy_bbmn

    Доброго дня. Близкий человек не вылезает из запоя. Жена на грани нервного срыва. В платной наркологии — бешеные счета. Итог, выручила эта служба — вывод из запоя недорого в Екатеринбурге. Купировали абстинентный синдром. В общем, контакты и стоимость тут — вывод из запоя на дому екатеринбург круглосуточно [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-vqx.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-vqx.ru[/url] Промедление может стоить здоровья. Вдруг это спасёт кого-то.

  3532. Vivod iz zapoya na domy_mzSi

    Всем салют. Человек в запое уже неделю. Жена плачет. В диспансер отвозить — позор на район. Короче, единственные кто приехал без предоплаты — анонимное выведение из запоя с капельницей. Врач осмотрел и начал детокс. В общем, жмите, чтобы не потерять — капельница от запоя на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru]капельница от запоя на дому[/url] Промедление может стоить жизни. Киньте ссылку нуждающимся.

  3533. alkoholizem_vlea

    Pozdravljeni, dragi moji. Moram povedati nekaj iz prve roke. Vsak dan je bil enak mucenje. Potem pa sem na spletu naletel na resitev. Govorim o odvajanju od alkohola pri Dr Vorobjev centru. Mislil sem, da mi nic ne more pomagati. Ampak sem dal tej metodi priloznost in zivljenje se je obrnilo na bolje. Vse uradne informacije in podrobnosti sem preveril na spletni strani, posodobljene podatke pa si lahko ogledate tukaj: Dr Vorobjev center [url=https://www.odvajanje-od-alkoho.com]https://www.odvajanje-od-alkoho.com[/url] Alkoholizem je bolezen in se zdravi.

    Ce vi sami potrebuje pomoc — vredno je poskusiti. Verjamem, da se da!

  3537. RexLot

    Solid value packed into a relatively short post, that takes skill, and a look at motherbloom continues the dense useful content across more pages, this site clearly understands that respecting reader time is itself a form of generosity which is something most blog operations seem to have forgotten lately across the wider open web.

  3538. RobertoDoday

    купить участок Ищете надежный участок под ферму с возможностью расширения границ в будущем? У нас есть уникальные предложения для развития вашего фермерского хозяйства.

  3539. Vivod iz zapoya na domy_xemn

    Привет из Екатеринбурга. Отец уже шестой день пьёт. Родственники не спят ночами. Скорая реагирует только на угрозу жизни. В общем, единственные кто приехал без лишних вопросов — вывод из запоя недорого в Екатеринбурге. К вечеру человек пришёл в сознание. В общем, контакты и стоимость тут — врач на дом капельница от запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-vqx.ru]врач на дом капельница от запоя[/url] Не медлите. Вдруг это спасёт кого-то.

  3541. Vivod iz zapoya na domy_yuSi

    Всем салют. Человек в запое уже неделю. Дети напуганы до смерти. Платная наркология — как счёт за квартиру. Короче, профессиональные врачи с горячими руками — недорогой вывод из запоя в Екатеринбурге. Сняли ломку и нормализовали давление. В общем, сохраните себе в закладки — нарколог вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru[/url] Не откладывайте. Киньте ссылку нуждающимся.

  3544. RobertSew

    санкции против России Следите за тем, как развивается санкционная повестка, с помощью наших графиков. Мы предоставляем только проверенную информацию из первых рук.

  3545. Williamloatt

    Летний лагерь с английским языком в YES Center — это полное погружение в среду. Дети общаются, играют и учатся одновременно, поэтому новые слова и фразы запоминаются легко, без зубрёжки. Опытные педагоги поддерживают каждого. Бронируйте места заранее.

  3546. alkoholizem_muea

    Pozdravljeni, dragi moji. Rad bi delil svojo zgodbo. Alkohol je dolgo casa vodil moje zivljenje. Potem pa sem od prijatelja izvedel za to moznost. Govorim o odvajanju od alkohola pri Dr Vorobjev centru. Bil sem preprican, da je zame prepozno. Ampak sem dal tej metodi priloznost in koncno sem spet jaz. Vec o tem in o celotnem postopku si lahko preberete neposredno na uradnem viru: zdravljenje alkoholizma [url=http://www.odvajanje-od-alkoho.com]zdravljenje alkoholizma[/url] Odvisnost od alkohola ni znak sibkosti.

    Ce vi sami se bori z alkoholom — to je lahko odlocilni korak. Nikoli ni prepozno za nov zacetek.

  3547. Vivod iz zapoya na domy_olmn

    Здарова, народ. Муж не встаёт с кровати. Родственники не спят ночами. В диспансер сдавать — ужас. В общем, выручила эта служба — вывод из запоя недорого в Екатеринбурге. Врач сразу поставил капельницу. В общем, вся информация по ссылке — нарколог на дом вывод [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-vqx.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-vqx.ru[/url] Звоните немедленно. Вдруг это спасёт кого-то.

  3548. RobertoDoday

    земельные участки в мо Земельные участки в МО — это выбор между близостью к городу или уединенностью в лесной глуши. Мы поможем найти именно то, что вы давно искали.

  3549. KyleAlors

    The tone stayed consistent across the whole post which is harder than it looks for longer pieces, and a look at brightnovahub continued the same voice, this kind of editorial consistency is a sign of either a single careful writer or a tightly run team and either is impressive today across the broader media environment.

  3551. Vivod iz zapoya na domy_mwMa

    Доброго вечера. Отец не встаёт с дивана. Жена в истерике. Платная клиника — грабёж среди бела дня. В итоге, единственные кто быстро приехал и помог — срочное выведение из запоя капельницей. Врач сразу поставил систему. В общем, не потеряйте, пригодится — поставить капельницу от запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru[/url] Не ждите. Вдруг кому-то это спасёт жизнь.

  3552. Narkologicheskaya pomosh_tnet

    Всем привет из Нижнего. Случилась беда. Соседи шепчутся за спиной. Скорая не считается с такой проблемой. В общем, единственные, кто взялся без нервотрёпки — наркологическая помощь недорого в Нижнем Новгороде. Сняли острую интоксикацию. В общем, телефон и цены тут — наркологическая клиника клиника помощь [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru]наркологическая клиника клиника помощь[/url] Не тяните с решением. Перешлите тем, кто в отчаянии.

  3553. Vivod iz zapoya na domy_qsKn

    Всем привет из НН. Близкий человек снова сорвался. Родня не знает, что делать. Скорая только забирает за 100 км. Короче, единственные, кто приехал без вопросов — анонимное выведение из запоя с капельницей. Через пару часов человек задышал ровно. В общем, сохраните себе — вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-nizhnij-novgorod-pwj.ru]вывод из запоя[/url] Не тяните время. Киньте ссылку нуждающимся.

  3554. Vivod iz zapoya na domy_ramn

    Доброго дня. Брат совсем потерял себя. Соседи уже начали звонить в участок. Скорая реагирует только на угрозу жизни. Итог, единственные кто приехал без лишних вопросов — анонимный вывод из запоя на дому. Врач сразу поставил капельницу. В общем, контакты и стоимость тут — нарколог капельницу на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-vqx.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-vqx.ru[/url] Звоните немедленно. Вдруг это спасёт кого-то.

  3555. Vivod iz zapoya na domy_xaSi

    Доброго времени. Отец не выходит из штопора. Жена плачет. Скорая не реагирует на пьянку. Короче, только эти ребята реально помогли — помощь нарколога на дому быстро. Через час человек начал говорить. В общем, жмите, чтобы не потерять — вывод из запоя круглосуточно [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru[/url] Звоните прямо сейчас. Может, кому-то она спасёт близкого.

  3557. alkoholizem_kkea

    Pozdravljeni, dragi moji. Rad bi delil svojo zgodbo. Vsak dan je bil enak mucenje. Potem pa sem na spletu naletel na resitev. Govorim o odvajanju od alkohola pri Dr Vorobjev centru. Mislil sem, da mi nic ne more pomagati. Ampak sem dal tej metodi priloznost in zivljenje se je obrnilo na bolje. Sam sem preucil celoten program in vsi kljucni podatki so na voljo na tej povezavi: alkoholizem [url=www.odvajanje-od-alkoho.com]alkoholizem[/url] Ni sramota prositi za pomoc.

    Ce vi sami ne vidi izhoda — prosim, ne odlasajte. Nikoli ni prepozno za nov zacetek.

  3558. Narkologicheskaya pomosh_pfet

    Доброго времени суток. Мой брат окончательно ушёл в запой. Жена места не находит. Скорая не считается с такой проблемой. Итог, выручила только эта клиника — наркологическая помощь на дому. К вечеру состояние стабилизировалось. В общем, все контакты по ссылке — наркологическая помощь цена [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru]https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru[/url] Звоните прямо сейчас. Вдруг это поможет кому-то.

  3560. RobertoDoday

    участок под ферму Ищете просторный участок под ферму для реализации аграрных проектов? В нашем каталоге представлены наделы с плодородной почвой и возможностью подключения коммуникаций.

  3561. Vivod iz zapoya na domy_sbMa

    Доброго вечера. Отец не встаёт с дивана. Дети всего боятся. Платная клиника — грабёж среди бела дня. Короче говоря, реально крутые специалисты — вывод из запоя цены адекватные. Врач сразу поставил систему. В общем, не потеряйте, пригодится — выведение из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru[/url] Не ждите. Вдруг кому-то это спасёт жизнь.

  3562. Vivod iz zapoya na domy_jqKn

    Здорова, народ. Брат не выходит из штопора. Родня не знает, что делать. Платная клиника просит бешеные деньги. Короче, реально профессиональные врачи — круглосуточный вывод из запоя с выездом. Врач поставил систему сразу. В общем, сохраните себе — вывод из запоя недорого [url=https://vyvod-iz-zapoya-na-domu-nizhnij-novgorod-pwj.ru]вывод из запоя недорого[/url] Промедление может стоить здоровья. Киньте ссылку нуждающимся.

  3565. CesarEpine

    Now recognising that the post handled the topic with appropriate technical precision without becoming dry, and a stop at primebazaarhub continued that balance, technical precision and readability are often in tension and this site has clearly figured out how to maintain both at once which is one of the harder editorial achievements in the form.

  3566. Vivod iz zapoya na domy_ptmn

    Здарова, народ. Отец уже шестой день пьёт. Соседи уже начали звонить в участок. В платной наркологии — бешеные счета. Итог, единственные кто приехал без лишних вопросов — профессиональная помощь на дому. К вечеру человек пришёл в сознание. В общем, вся информация по ссылке — наркология вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-vqx.ru]наркология вывод из запоя[/url] Промедление может стоить здоровья. Вдруг это спасёт кого-то.

  3567. Narkologicheskaya pomosh_jaet

    Доброго времени суток. Отец уже вторую неделю не просыхает. Дети боятся оставаться дома. Скорая не считается с такой проблемой. Итог, единственные, кто взялся без нервотрёпки — плановая наркологическая помощь без очередей. Сняли острую интоксикацию. В общем, все контакты по ссылке — наркологическая клиника недорого [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru]https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru[/url] Не тяните с решением. Вдруг это поможет кому-то.

  3568. Vivod iz zapoya na domy_teSi

    Привет из Екатеринбурга. Отец не выходит из штопора. Жена плачет. Платная наркология — как счёт за квартиру. Короче, только эти ребята реально помогли — вывод из запоя на дому срочный. Врач осмотрел и начал детокс. В общем, жмите, чтобы не потерять — вывести из запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru]вывести из запоя[/url] Звоните прямо сейчас. Киньте ссылку нуждающимся.

  3569. Kapelnica ot zapoya_slPn

    Всем привет из НН. Близкий человек уже неделю в запое. Дети испуганы. В бесплатную наркологию — страшно идти. Короче, спасла только эта капельница — капельница от запоя цена доступная. К утру человек пришёл в себя. В общем, жмите, чтобы сохранить — капельница на дому нижний новгород от алкоголя [url=https://kapelnica-ot-zapoya-nizhnij-novgorod-icy.ru]https://kapelnica-ot-zapoya-nizhnij-novgorod-icy.ru[/url] Каждый час без капельницы ухудшает состояние. Вдруг это поможет.

  3570. Vivod iz zapoya na domy_dmMa

    Здорова, народ. Брат снова ушел в штопор. Жена в истерике. В наркологию везти — страшно. В итоге, спасла только эта бригада — срочное выведение из запоя капельницей. Врач сразу поставил систему. В общем, вся инфа и контакты по ссылке — прокапаться от алкоголя на дому [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru[/url] Звоните прямо сейчас. Отправьте тем, кто рядом с бедой.

  3571. Narkologicheskaya pomosh_erMl

    Доброго дня. Брат уже пятые сутки не просыхает. Соседи уже стучат в стену. Платная клиника — огромные счета. Итог, единственные, кто быстро отреагировал — наркологическая помощь на дому срочно. Приехали через 35 минут. В общем, все контакты по ссылке — частная наркологическая помощь [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-fql.ru]частная наркологическая помощь[/url] Каждый час усугубляет ситуацию. Вдруг это спасёт жизнь.

  3577. AugustAmind

    автоэксперт ДТП Помощь аварийного комиссара при ДТП в Хабаровске особенно востребована в ситуациях, когда необходимо быстро и правильно оформить происшествие. Специалист оценит обстоятельства аварии, подготовит необходимые документы, проконсультирует по вопросам страхового возмещения и поможет выбрать оптимальный порядок оформления.

  3578. Vivod iz zapoya na domy_nnKn

    Здорова, народ. Близкий человек снова сорвался. Соседи уже начали коситься. Платная клиника просит бешеные деньги. Короче, единственные, кто приехал без вопросов — недорогой вывод из запоя в Нижнем Новгороде. Прибыли через 40 минут. В общем, вся инфа и контакты по ссылке — прокапаться от алкоголя на дому нижний новгород [url=https://vyvod-iz-zapoya-na-domu-nizhnij-novgorod-pwj.ru]https://vyvod-iz-zapoya-na-domu-nizhnij-novgorod-pwj.ru[/url] Промедление может стоить здоровья. Киньте ссылку нуждающимся.

  3579. JeromeZip

    Started reading expecting to disagree and ended mostly nodding along, and a look at agavebarley continued the pattern, content that wins agreement through evidence and reasoning rather than rhetorical force is the kind that actually shifts minds and this site clearly knows how to do that across what I have read so far.

  3581. Narkologicheskaya pomosh_fpet

    Доброго времени суток. Мой брат окончательно ушёл в запой. Дети боятся оставаться дома. Государственные клиники — только учёт и очереди. Итог, выручила только эта клиника — частная наркологическая помощь с выездом. Сняли острую интоксикацию. В общем, телефон и цены тут — наркологическая клиника анонимная помощь нарколога [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru]https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru[/url] Звоните прямо сейчас. Перешлите тем, кто в отчаянии.

  3583. alkoholizem_vsea

    Zivjo vsem skupaj. Danes bi rad spregovoril o necem pomembnem. Bil sem ujetnik odvisnosti. Potem pa sem po dolgem iskanju koncno nasel pravo pot. Govorim o zdravljenju alkoholizma pri Dr Vorobjevu. Sprva nisem verjel. Ampak sem se odlocil за ta korak in koncno sem spet jaz. Vse uradne informacije in podrobnosti sem preveril na spletni strani, posodobljene podatke pa si lahko ogledate tukaj: odvisnost od alkohol [url=http://odvajanje-od-alkoho.com]odvisnost od alkohol[/url] Odvisnost od alkohola ni znak sibkosti.

    Ce vas partner ne vidi izhoda — to je lahko odlocilni korak. Nikoli ni prepozno za nov zacetek.

  3584. Kapelnica ot zapoya_qePn

    Приветствую всех. Ситуация жёсткая. Жена в отчаянии. Скорая не считается с запоями. Короче, реально помогли эти врачи — прокапаться на дому от алкоголя цена фиксированная. К утру человек пришёл в себя. В общем, цены и телефон тут — капельница при алкогольной интоксикации на дому цена [url=https://kapelnica-ot-zapoya-nizhnij-novgorod-icy.ru]капельница при алкогольной интоксикации на дому цена[/url] Не ждите чуда. Киньте ссылку тем, кто в беде.

  3585. Charlessak

    On reflection this is the kind of writing that improves my taste for what is possible in the format, and a look at professionalix continued raising that bar, content that elevates my expectations rather than lowering them is doing important work in calibrating my standards and this site is participating in that elevation reliably.

  3586. Christophermaf

    Just want to acknowledge that the writing here is doing something right, and a quick visit to jewelbrookmerchantgallery confirmed the same standards run across the broader site, recognising good work is something I try to do when I find it because the alternative is silence and silence rewards mediocrity.

  3587. Vivod iz zapoya v stacionare_kjPl

    Всем привет. Ситуация критическая. Нужно серьёзное наблюдение специалистов. Платные клиники — дорого и непонятно. Короче, действительно эффективный метод — вывод из запоя нижний новгород стационар. Положили в палату на три дня. В общем, телефон и цены тут — круглосуточный стационар вывод из запоя [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-knd.ru]https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-knd.ru[/url] Стационар — это шанс на нормальную жизнь. Это может спасти чью-то семью.

  3588. Vivod iz zapoya na domy_onMa

    Всем привет. Муж не выходит из комнаты. Соседи уже стучат в дверь. Скорая помощь просто разводит руками. В итоге, спасла только эта бригада — вывод из запоя цены адекватные. Сняли алкогольную интоксикацию. В общем, не потеряйте, пригодится — врач на дом капельница от запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru[/url] Не ждите. Вдруг кому-то это спасёт жизнь.

  3589. Israelesode

    советы Roblox Сайт с гайдами по Roblox — прокачай свои навыки быстрее вместе с https://rxworld.net/! Здесь ты найдёшь коды, секреты, советы и лучшие стратегии для популярных режимов Roblox. Регулярные обновления, полезные фишки и помощь как новичкам, так и опытным игрокам.

  3594. Narkologicheskaya pomosh_qqMl

    Всем здравствуйте. Отец снова ушёл в штопор. Соседи уже стучат в стену. В диспансер тащить — позор на район. В общем, единственные, кто быстро отреагировал — анонимная наркологическая частная клиника. Приехали через 35 минут. В общем, жмите, чтобы сохранить — наркологическая помощь наркология [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-fql.ru]наркологическая помощь наркология[/url] Не медлите. Отправьте тем, кто рядом с бедой.

  3595. Narkologicheskaya pomosh_zbet

    Здорова, ребята. Близкий человек полностью потерял контроль. Родственники не знают, что предпринять. Частные центры ломят космические суммы. Итог, единственные, кто взялся без нервотрёпки — наркологическая помощь недорого в Нижнем Новгороде. Сняли острую интоксикацию. В общем, телефон и цены тут — анонимная наркологическая помощь нарколог [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru]https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru[/url] Каждый день усугубляет ситуацию. Вдруг это поможет кому-то.

  3597. Stuartmox

    I really like the calm tone here, it does not push anything on the reader, and after I went through directshoppinghub I felt the same way, just steady useful content laid out without drama, which is exactly what someone trying to learn something quickly needs to find rather than aggressive marketing.

  3598. MasonFrids

    My usual response to new bookmarks is to forget them but this one I have already returned to twice, and a look at dyleko pulled me back a third time, the actual return rate to bookmarked sites is the real measure of value and this one is clearing that measure at a notable rate already.

  3600. Vivod iz zapoya na domy_heKn

    Доброго дня. Беда пришла. Родня не знает, что делать. Платная клиника просит бешеные деньги. Короче, реально профессиональные врачи — анонимное выведение из запоя с капельницей. Через пару часов человек задышал ровно. В общем, вся инфа и контакты по ссылке — вывод из запоя на дому нижний новгород круглосуточно [url=https://vyvod-iz-zapoya-na-domu-nizhnij-novgorod-pwj.ru]https://vyvod-iz-zapoya-na-domu-nizhnij-novgorod-pwj.ru[/url] Звоните прямо сейчас. Киньте ссылку нуждающимся.

  3601. Kapelnica ot zapoya_ilPn

    Доброго времени. Отец снова сорвался в пьянку. Родственники не знают, как помочь. Скорая не считается с запоями. Короче, единственные, кто быстро приехал и поставил систему — капельница от запоя цена доступная. Сняли острую интоксикацию. В общем, цены и телефон тут — прокапаться от алкоголя [url=https://kapelnica-ot-zapoya-nizhnij-novgorod-icy.ru]прокапаться от алкоголя[/url] Не ждите чуда. Киньте ссылку тем, кто в беде.

  3602. Vivod iz zapoya na domy_ncMa

    Привет из Екб. Брат снова ушел в штопор. Жена в истерике. Платная клиника — грабёж среди бела дня. В итоге, единственные кто быстро приехал и помог — вывод из запоя цены адекватные. Приехали через 30 минут. В общем, жмите, чтобы сохранить — вывод из запоя на дому в екатеринбурге [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru[/url] Каждый час усугубляет состояние. Отправьте тем, кто рядом с бедой.

  3603. Vivod iz zapoya v stacionare_sfPl

    Привет из Нижнего. Отец окончательно ушёл в штопор. Нужно серьёзное наблюдение специалистов. Платные клиники — дорого и непонятно. Короче, спасло только это — вывод из запоя стационарно под контролем врачей. Врачи наблюдали 24/7. В общем, вся инфа по ссылке — круглосуточный стационар вывод из запоя [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-knd.ru]https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-knd.ru[/url] Стационар — это шанс на нормальную жизнь. Перешлите тем, кто в отчаянии.

  3605. Narkologicheskaya pomosh_zbet

    Приветствую. Мой брат окончательно ушёл в запой. Жена места не находит. Скорая не считается с такой проблемой. В общем, выручила только эта клиника — платная наркологическая помощь с гарантией. Врач осмотрел и начал капельницу. В общем, жмите, чтобы сохранить — анонимная наркологическая помощь нарколог [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru]https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru[/url] Звоните прямо сейчас. Перешлите тем, кто в отчаянии.

  3606. Narkologicheskaya pomosh_khMl

    Всем здравствуйте. Отец снова ушёл в штопор. Мать рыдает. В диспансер тащить — позор на район. В общем, единственные, кто быстро отреагировал — наркологическая помощь недорого в Нижнем Новгороде. Врач осмотрел и поставил капельницу. В общем, не потеряйте — анонимная наркологическая помощь нарколог [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-fql.ru]https://narkologicheskaya-pomoshh-nizhnij-novgorod-fql.ru[/url] Каждый час усугубляет ситуацию. Вдруг это спасёт жизнь.

  3607. Gunnerevese

    Going to share this with a friend who has been asking the same questions for a while now, and a stop at urgesnare added a few more pages I will pass along too, this is the kind of generous information that earns a small thank you from me right now and again later this week.

  3608. Gunnergek

    Without comparing too aggressively to other sources this one stands out for the right reasons, and a look at ekomug continued that distinctive quality, content that distinguishes itself through substance rather than style tricks is content with lasting differentiation and this site has clearly chosen substance based differentiation as its core editorial strategy.

  3610. Kapelnica ot zapoya_jhPn

    Доброго времени. Брат не выходит из штопора. Соседи уже начали звонить в полицию. В бесплатную наркологию — страшно идти. Короче, единственные, кто быстро приехал и поставил систему — прокапаться от алкоголя недорого. К утру человек пришёл в себя. В общем, жмите, чтобы сохранить — прокапаться от алкоголя цены [url=https://kapelnica-ot-zapoya-nizhnij-novgorod-icy.ru]прокапаться от алкоголя цены[/url] Звоните прямо сейчас. Вдруг это поможет.

  3611. Vivod iz zapoya na domy_zdKn

    Приветствую земляков. Беда пришла. Дети плачут по ночам. В диспансер тащить — клеймо на всю жизнь. Короче, выручила эта служба — недорогой вывод из запоя в Нижнем Новгороде. Врач поставил систему сразу. В общем, жмите, чтобы не потерять — выведение из запоя в нижнем новгороде [url=https://vyvod-iz-zapoya-na-domu-nizhnij-novgorod-pwj.ru]https://vyvod-iz-zapoya-na-domu-nizhnij-novgorod-pwj.ru[/url] Не тяните время. Вдруг это спасёт чью-то жизнь.

  3615. Vivod iz zapoya na domy_phMa

    Здорова, народ. Просто ужас. Жена в истерике. В наркологию везти — страшно. В итоге, спасла только эта бригада — круглосуточный вывод из запоя с выездом. К ночи человек пришёл в себя. В общем, телефон и расценки тут — вывод из запоя на дому круглосуточно [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru[/url] Не ждите. Отправьте тем, кто рядом с бедой.

  3617. DaxSef

    Quietly the post solved something I had been turning over without quite knowing how to phrase the question, and a look at ideasrequiremovement extended that quiet solving, content that addresses unformulated needs is content with reader insight and this site has demonstrated that insight at a high rate across the pieces I have read recently.

  3618. Narkologicheskaya pomosh_axet

    Здорова, ребята. Отец уже вторую неделю не просыхает. Родственники не знают, что предпринять. Государственные клиники — только учёт и очереди. В общем, единственные, кто взялся без нервотрёпки — плановая наркологическая помощь без очередей. Врач осмотрел и начал капельницу. В общем, жмите, чтобы сохранить — наркологическая помощь недорого [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru]https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru[/url] Звоните прямо сейчас. Перешлите тем, кто в отчаянии.

  3619. Vivod iz zapoya v stacionare_dcPl

    Привет из Нижнего. Близкий человек потерял контроль над собой. Домашние условия не помогают. Платные клиники — дорого и непонятно. Короче, спасло только это — вывод из запоя в стационаре круглосуточно. Положили в палату на три дня. В общем, вся инфа по ссылке — наркология вывод из запоя в стационаре [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-knd.ru]наркология вывод из запоя в стационаре[/url] Не надейтесь, что само пройдёт. Перешлите тем, кто в отчаянии.

  3620. Jimbop

    Quietly enjoying that I have found a new site to follow for the topic, and a look at reliableshoppinghub reinforced the small pleasure of the find, the discovery of new high quality sources is one of the more durable pleasures of careful internet reading and this site has been generating that discovery pleasure at multiple points already today.

  3623. Jimmyhok

    Useful information presented in a way that does not feel like a sales pitch, that is what I appreciated most, and a stop at sprucetrill was the same, no upsell and no fake urgency just steady content laid out properly for someone trying to actually learn from it rather than just be sold to.

  3624. Kapelnica ot zapoya_yjPn

    Здорова, ребята. Ситуация жёсткая. Родственники не знают, как помочь. Платная клиника — деньги на ветер. Короче, единственные, кто быстро приехал и поставил систему — поставить капельницу от запоя на дому цена адекватная. Приехали через 45 минут. В общем, не потеряйте — капельница на дому нижний новгород от алкоголя [url=https://kapelnica-ot-zapoya-nizhnij-novgorod-icy.ru]https://kapelnica-ot-zapoya-nizhnij-novgorod-icy.ru[/url] Не ждите чуда. Киньте ссылку тем, кто в беде.

  3625. Narkologicheskaya pomosh_twMl

    Доброго дня. Близкий человек сорвался в запой. Родственники не знают, что предпринять. Платная клиника — огромные счета. В общем, реально профессиональные врачи — наркологическая помощь недорого в Нижнем Новгороде. Врач осмотрел и поставил капельницу. В общем, жмите, чтобы сохранить — платная наркологическая помощь [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-fql.ru]платная наркологическая помощь[/url] Каждый час усугубляет ситуацию. Вдруг это спасёт жизнь.

  3627. Stephencip

    Without comparing too aggressively to other sources this one stands out for the right reasons, and a look at ekooat continued that distinctive quality, content that distinguishes itself through substance rather than style tricks is content with lasting differentiation and this site has clearly chosen substance based differentiation as its core editorial strategy.

  3629. Narkologicheskaya pomosh_yxet

    Всем привет из Нижнего. Отец уже вторую неделю не просыхает. Соседи шепчутся за спиной. Частные центры ломят космические суммы. Итог, реально профессиональная бригада врачей — частная наркологическая помощь с выездом. К вечеру состояние стабилизировалось. В общем, жмите, чтобы сохранить — анонимная наркологическая частная клиника [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru]https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru[/url] Не тяните с решением. Перешлите тем, кто в отчаянии.

  3630. Vivod iz zapoya na domy_dvMa

    Здорова, народ. Отец не встаёт с дивана. Дети всего боятся. Скорая помощь просто разводит руками. В итоге, единственные кто быстро приехал и помог — вывод из запоя цены адекватные. К ночи человек пришёл в себя. В общем, жмите, чтобы сохранить — вывод из запоя в екатеринбурге [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru[/url] Не ждите. Вдруг кому-то это спасёт жизнь.

  3631. Vivod iz zapoya na domy_mnKn

    Всем привет из НН. Мой отец уже четвёртый день в запое. Родня не знает, что делать. Скорая только забирает за 100 км. Короче, единственные, кто приехал без вопросов — недорогой вывод из запоя в Нижнем Новгороде. Сняли абстинентный синдром. В общем, жмите, чтобы не потерять — капельница от запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-nizhnij-novgorod-pwj.ru]https://vyvod-iz-zapoya-na-domu-nizhnij-novgorod-pwj.ru[/url] Промедление может стоить здоровья. Киньте ссылку нуждающимся.

  3636. Vivod iz zapoya v stacionare_ruPl

    Привет из Нижнего. Отец окончательно ушёл в штопор. Нужно серьёзное наблюдение специалистов. Скорая не решает проблему глобально. Короче, действительно эффективный метод — вывод из запоя стационарно под контролем врачей. Положили в палату на три дня. В общем, телефон и цены тут — наркология вывод из запоя в стационаре [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-knd.ru]наркология вывод из запоя в стационаре[/url] Не надейтесь, что само пройдёт. Это может спасти чью-то семью.

  3637. Kapelnica ot zapoya_djPn

    Приветствую всех. Близкий человек уже неделю в запое. Жена в отчаянии. В бесплатную наркологию — страшно идти. Короче, единственные, кто быстро приехал и поставил систему — прокапаться от алкоголя цены ниже рынка. Приехали через 45 минут. В общем, цены и телефон тут — капельница при алкогольной интоксикации на дому цена [url=https://kapelnica-ot-zapoya-nizhnij-novgorod-icy.ru]капельница при алкогольной интоксикации на дому цена[/url] Не ждите чуда. Вдруг это поможет.

  3638. JaceGen

    Did not expect much when I clicked through but ended up reading the whole thing carefully, and a stop at ideasguidedforward kept that engagement going, sometimes the unassuming sites turn out to deliver more than the flashy ones which is something I have learned to look out for over time online lately and across topics.

  3639. Riversog

    A clear cut above the usual noise on the subject, and a look at tracetrifle only made that gap wider in my view, the kind of place that earns its visitors through quality rather than through aggressive marketing or sponsored placements which is increasingly the only way most sites stay afloat across the modern web.

  3640. Arnoldmow

    Really grateful for content like this, it does not waste my time and it does not insult my intelligence either, and a quick look at eloido was the same, balanced respectful writing that makes a person feel welcome rather than rushed through pages of forced engagement just to keep clicking around.

  3641. Narkologicheskaya pomosh_ktMl

    Здорова, народ. Беда случилась. Соседи уже стучат в стену. Скорая не считает это проблемой. В общем, реально профессиональные врачи — анонимная наркологическая частная клиника. К вечеру состояние нормализовалось. В общем, цены и телефон тут — помощь наркологическая [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-fql.ru]помощь наркологическая[/url] Каждый час усугубляет ситуацию. Отправьте тем, кто рядом с бедой.

  3644. Narkologicheskaya pomosh_obet

    Доброго времени суток. Случилась беда. Родственники не знают, что предпринять. Частные центры ломят космические суммы. В общем, реально профессиональная бригада врачей — платная наркологическая помощь с гарантией. Приехали в течение часа. В общем, все контакты по ссылке — наркологическая помощь [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-ksc.ru]наркологическая помощь[/url] Звоните прямо сейчас. Вдруг это поможет кому-то.

  3645. DorianNof

    Thank you for keeping the writing honest and the points easy to verify against your own experience, and a stop at shoptrailmarket reflected the same approach, no exaggeration just steady useful content that I can take with me into my own work without second guessing every sentence I happen to read here.

  3648. Kapelnica ot zapoya_gtPn

    Здорова, ребята. Отец снова сорвался в пьянку. Соседи уже начали звонить в полицию. В бесплатную наркологию — страшно идти. Короче, реально помогли эти врачи — поставить капельницу от запоя на дому цена адекватная. Врач сразу начал детокс. В общем, не потеряйте — поставить капельницу от запоя на дому цена [url=https://kapelnica-ot-zapoya-nizhnij-novgorod-icy.ru]поставить капельницу от запоя на дому цена[/url] Звоните прямо сейчас. Киньте ссылку тем, кто в беде.

  3649. Vivod iz zapoya na domy_ooMa

    Здорова, народ. Отец не встаёт с дивана. Родственники на взводе. Скорая помощь просто разводит руками. В итоге, единственные кто быстро приехал и помог — недорогой вывод из запоя в Екатеринбурге. Врач сразу поставил систему. В общем, не потеряйте, пригодится — выведение из запоя екатеринбург [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru[/url] Не ждите. Вдруг кому-то это спасёт жизнь.

  3650. Vivod iz zapoya na domy_oySr

    Доброго времени суток. Случилась беда. Соседи уже начали стучать в стену. Платная клиника просит бешеные деньги. Короче, единственные, кто быстро приехал — срочный вывод из запоя с выездом. Сняли острую интоксикацию. В общем, жмите, чтобы сохранить — вывод из запоя с выездом на дом [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru[/url] Не ждите чуда. Киньте ссылку тем, кто в беде.

  3651. Vivod iz zapoya na domy_fmSi

    Привет из Екатеринбурга. Отец не выходит из штопора. Жена плачет. Скорая не реагирует на пьянку. Короче, профессиональные врачи с горячими руками — недорогой вывод из запоя в Екатеринбурге. Врач осмотрел и начал детокс. В общем, сохраните себе в закладки — вывод из запоя на дому цена [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru[/url] Звоните прямо сейчас. Может, кому-то она спасёт близкого.

  3652. 888starz_uxsa

    يتسم ملف apk بخفّة الحجم مما يجعله مناسبًا لمختلف أجهزة أندرويد.
    888starz تحميل [url=theracingbicycle.com]https://theracingbicycle.com/[/url]
    قبل تثبيت apk على أندرويد ينبغي تفعيل السماح بالتثبيت من مصادر خارجية.
    يضمن apk أداءً سلسًا على الأجهزة القديمة والحديثة على حد سواء.
    يُستحسن التحقق من صلاحيات apk عند تثبيته للحفاظ على خصوصية البيانات.
    يدعم 888starz أجهزة iOS ليتمكن مستخدمو الآيفون من تثبيت التطبيق بسهولة.

  3653. 888starz_elOa

    يقدم الموقع الرسمي لـ 888starz في مصر تجربة شاملة تجمع بين ألعاب الكازينو والرهان الرياضي.
    تُعرض أحدث ألعاب السلوت والعناوين الأكثر شعبية في مقدمة صفحة الكازينو.
    888starz [url=http://free-credits-report.com/]https://free-credits-report.com/[/url]
    تتوفر خطوط مراهنة على الدوريات العالمية والمحلية بما فيها بطولات مصر.
    يحصل المستخدمون الجدد على مكافأة ترحيب حتى 1500 يورو إضافة إلى 150 فري سبين عند التسجيل.
    يمكن التسجيل في الموقع الرسمي عبر الهاتف أو البريد الإلكتروني أو بنقرة واحدة خلال دقائق.

  3654. Vivod iz zapoya na domy_pcPr

    Здорова, народ. Отец не выходит из штопора. Соседи уже стучат в стену. В государственный диспансер — табу. В итоге, выручила эта служба — капельница на дому от запоя. Сняли острую интоксикацию. В общем, жмите, чтобы сохранить — вывести из запоя цена [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-mnq.ru]вывести из запоя цена[/url] Звоните прямо сейчас. Вдруг это спасёт чью-то семью.

  3655. Vivod iz zapoya na domy_beMt

    Доброго дня, земляки. Кошмар полный. Соседи уже вызывали участкового. Скорая не считается с запоями. Итог, реально крутые врачи — выведение из запоя на дому анонимно. К утру человек пришёл в сознание. В общем, все контакты по ссылке — вывода из запоя 24 [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-xyt.ru]вывода из запоя 24[/url] Не тяните время. Вдруг это спасёт чью-то жизнь.

  3656. Vivod iz zapoya na domy_fssr

    Питер, привет. Мой отец уже третьи сутки в запое. Родственники не знают, за что хвататься. Скорая не приедет на такой вызов. Короче, реально профессиональные врачи — круглосуточный вывод из запоя с выездом. Приехали через 35 минут. В общем, жмите, чтобы сохранить — вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru]вывод из запоя[/url] Звоните прямо сейчас. Вдруг это спасёт чью-то жизнь.

  3657. Vivod iz zapoya na domy_lami

    Доброго времени, земляки. Близкий человек уже пятые сутки в запое. Мать на грани нервного срыва. В диспансер везти — позор на район. Короче, единственные, кто приехал быстро — недорогой вывод из запоя в Питере. Приехали за 30 минут. В общем, жмите, чтобы сохранить — помощь вывода запоя [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-jfw.ru]помощь вывода запоя[/url] Звоните прямо сейчас. Перешлите тем, кто рядом с бедой.

  3658. 888starz_hskl

    يقدم الموقع تصميمًا عربيًا مريحًا يسهّل الوصول إلى الكازينو والرياضة بنقرات قليلة.

    تتجاوز مكتبة الكازينو 7000 لعبة تشمل السلوت والطاولات من مزودين مثل Play’n GO و Evolution.

    يغطي الموقع تشكيلة رياضية واسعة تضم كرة القدم والتنس والملاكمة والرياضات الإلكترونية.

    يحصل المشتركون الجدد على مكافأة أولى تبلغ حتى 1500 دولار إلى جانب دورات سلوت مجانية.

    يتيح 888starz إيداعًا وسحبًا عبر فيزا وماستركارد ومحافظ رقمية وعشرات العملات الرقمية.

    888starz [url=http://www.aclknights.com]https://aclknights.com/[/url]

  3659. Vivod iz zapoya v stacionare_esPl

    Здорова, народ. Мой брат уже неделю в запое. Нужно серьёзное наблюдение специалистов. Государственная наркология — страшно и стыдно. Короче, спасло только это — анонимный вывод из запоя в стационаре. Врачи наблюдали 24/7. В общем, телефон и цены тут — вывод из запоя в стационаре [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-knd.ru]вывод из запоя в стационаре[/url] Стационар — это шанс на нормальную жизнь. Перешлите тем, кто в отчаянии.

  3661. Robinengew

    If I am being honest this is the kind of site I quietly hope my own work will someday resemble, and a stop at torquetiara extended that aspirational feeling, finding work that models what I want to produce is part of why I read carefully and this site has been performing that modelling function for me lately consistently.

  3662. TomMum

    A piece that reads as if the writer trusted readers to fill in obvious gaps, and a look at elonox continued that respectful approach, content that does not over explain what the reader can infer is content that respects intelligence and this site has clearly chosen to write to capable readers rather than to the lowest common denominator.

  3663. Vivod iz zapoya na domy_fuKn

    Всем привет из НН. Беда пришла. Родня не знает, что делать. Платная клиника просит бешеные деньги. Короче, реально профессиональные врачи — помощь нарколога на дом. Через пару часов человек задышал ровно. В общем, сохраните себе — снятие алкогольной интоксикации нижний новгород [url=https://vyvod-iz-zapoya-na-domu-nizhnij-novgorod-pwj.ru]https://vyvod-iz-zapoya-na-domu-nizhnij-novgorod-pwj.ru[/url] Звоните прямо сейчас. Киньте ссылку нуждающимся.

  3664. Narkologicheskaya pomosh_ggMl

    Привет из Нижнего. Близкий человек сорвался в запой. Соседи уже стучат в стену. Платная клиника — огромные счета. В общем, реально профессиональные врачи — наркологическая помощь недорого в Нижнем Новгороде. К вечеру состояние нормализовалось. В общем, жмите, чтобы сохранить — наркологическая помощь наркология [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-fql.ru]наркологическая помощь наркология[/url] Звоните прямо сейчас. Отправьте тем, кто рядом с бедой.

  3665. Colinhal

    Thanks for the practical examples scattered through the post rather than abstract theory only, and a look at forwardmovementengine continued that grounded style, abstract points are easier to remember when paired with concrete situations and the writers here clearly understand how readers actually retain information from blog content reading sessions.

  3669. Vivod iz zapoya na domy_yqsr

    Всем привет с Невы. Близкий человек снова сорвался. Дети боятся отца. Скорая не приедет на такой вызов. Короче, единственные, кто быстро приехал — недорогой вывод из запоя в Санкт-Петербурге. Через пару часов человек пришёл в себя. В общем, жмите, чтобы сохранить — помощь вывода запоя [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru[/url] Звоните прямо сейчас. Вдруг это спасёт чью-то жизнь.

  3670. Vivod iz zapoya na domy_orSi

    Привет из Екатеринбурга. Брат совсем потерял человеческий облик. Жена плачет. Платная наркология — как счёт за квартиру. Короче, единственные кто приехал без предоплаты — круглосуточный вывод из запоя на дом. Прибыли через полчаса. В общем, все контакты по ссылке — нарколог на дом вывод [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru[/url] Не откладывайте. Может, кому-то она спасёт близкого.

  3672. Vivod iz zapoya na domy_fdSr

    Доброго времени суток. Случилась беда. Мать на грани истерики. Платная клиника просит бешеные деньги. Короче, выручила эта служба — вывод из запоя на дому круглосуточно. Врач сразу поставил систему. В общем, жмите, чтобы сохранить — выведение из запоя в спб [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru[/url] Каждый час ухудшает состояние. Киньте ссылку тем, кто в беде.

  3673. Vivod iz zapoya na domy_lsmi

    Всем привет из северной столицы. Отец не выходит из штопора. Родственники не знают, как помочь. Платная клиника — бешеные счета. Короче, реально крутые врачи попались — капельница от запоя на дому. Приехали за 30 минут. В общем, не потеряйте — нарколог вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-jfw.ru]нарколог вывод из запоя[/url] Не ждите чуда. Вдруг это спасёт чью-то жизнь.

  3675. Vivod iz zapoya na domy_qtPr

    Здорова, народ. Отец не выходит из штопора. Соседи уже стучат в стену. Платная клиника — грабёж. В итоге, реально крутые специалисты — выведение из запоя на дому анонимно. Сняли острую интоксикацию. В общем, жмите, чтобы сохранить — нарколог вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-mnq.ru]нарколог вывод из запоя[/url] Не ждите, пока станет хуже. Перешлите тем, кто рядом с бедой.

  3676. ShawnHiedo

    Felt this in a way I cannot quite explain, the topic just hit different here, and a stop at smartbuyingzone continued in that vein, sometimes you find a site whose perspective lines up with how you have been thinking and reading their work feels like a small relief which I appreciated more than I expected.

  3678. Vivod iz zapoya na domy_sgMt

    Приветствую народ. Отец не выходит из штопора. Соседи уже вызывали участкового. Скорая не считается с запоями. Итог, реально крутые врачи — круглосуточный вывод из запоя с выездом. Сняли абстинентный синдром. В общем, жмите, чтобы сохранить — круглосуточный вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-xyt.ru]круглосуточный вывод из запоя[/url] Звоните прямо сейчас. Киньте ссылку нуждающимся.

  3679. Robertniply

    One of the more honest takes on the topic I have seen lately, no spin and no oversell, and a stop at elucan kept that going, the kind of voice the open web could use a lot more of rather than the endless echo chamber of recycled opinions floating around every social platform these days.

  3680. GarrettNiG

    Glad to find something on this topic that does not start with three paragraphs of throat clearing before getting to the point, and a stop at turbanshade also dives right in, respect for the readers time shows up in small editorial choices like this and they add up to a real difference quickly.

  3681. Vivod iz zapoya v stacionare_cjPl

    Доброго вечера. Близкий человек потерял контроль над собой. Нужно серьёзное наблюдение специалистов. Скорая не решает проблему глобально. Короче, действительно эффективный метод — наркология вывод из запоя в стационаре. Капельницы и препараты подбирали индивидуально. В общем, телефон и цены тут — выведение из запоя в стационаре [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-knd.ru]выведение из запоя в стационаре[/url] Не надейтесь, что само пройдёт. Это может спасти чью-то семью.

  3683. Vivod iz zapoya na domy_rjKn

    Приветствую земляков. Близкий человек снова сорвался. Родня не знает, что делать. Платная клиника просит бешеные деньги. Короче, реально профессиональные врачи — недорогой вывод из запоя в Нижнем Новгороде. Сняли абстинентный синдром. В общем, жмите, чтобы не потерять — капельница от запоя на дому круглосуточно [url=https://vyvod-iz-zapoya-na-domu-nizhnij-novgorod-pwj.ru]капельница от запоя на дому круглосуточно[/url] Промедление может стоить здоровья. Киньте ссылку нуждающимся.

  3684. 888starz_jxMn

    Rasmiy saytga kirish orqali foydalanuvchilar barcha o’yin va tikish bo’limlaridan foydalanishlari mumkin.

    Rasmiy saytda jonli dilerli kazino bo’limi real dilerlar bilan o’ynash imkonini beradi.

    Rasmiy saytda jonli tikish koeffitsiyentlari o’yin davomida real vaqtda yangilanadi.

    888starz [url=https://archevore.com/888starz-royxatdan-otish-jarayoni-xush-kelibsiz-bonuslari/]888starz[/url].

  3685. Vivod iz zapoya na domy_ruMa

    Здорова, народ. Отец не встаёт с дивана. Соседи уже стучат в дверь. В наркологию везти — страшно. В итоге, реально крутые специалисты — помощь нарколога на дом. Врач сразу поставил систему. В общем, не потеряйте, пригодится — выезд на дом капельница от запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-mfk.ru[/url] Каждый час усугубляет состояние. Вдруг кому-то это спасёт жизнь.

  3686. Narkologicheskaya pomosh_qrMl

    Здорова, народ. Беда случилась. Мать рыдает. Скорая не считает это проблемой. В общем, единственные, кто быстро отреагировал — платная наркологическая помощь с выездом. К вечеру состояние нормализовалось. В общем, все контакты по ссылке — наркологическая помощь [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-fql.ru]наркологическая помощь[/url] Каждый час усугубляет ситуацию. Вдруг это спасёт жизнь.

  3687. Vivod iz zapoya na domy_fvsr

    Здорова, народ. Мой отец уже третьи сутки в запое. Дети боятся отца. В наркологию тащить — страшно. Короче, реально профессиональные врачи — недорогой вывод из запоя в Санкт-Петербурге. Через пару часов человек пришёл в себя. В общем, жмите, чтобы сохранить — капельница от алкоголя на дому спб [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru[/url] Каждый час ухудшает состояние. Вдруг это спасёт чью-то жизнь.

  3688. 888starz apk_kxPt

    888starz yuklab olish [url=https://1in11.org/]888starz yuklab olish[/url]

    888starz o’zbek o’yinchilariga kazino, jonli o’yinlar va sport stavkalarini bir manzilda ochib beradi.

    Aviator, Keno, Wheel va Bingo kabi tezkor o’yinlar alohida bo’limda to’plangan.

    Real vaqt rejimidagi tikish yuqori koeffitsiyentlar bilan taqdim etiladi.

    Saytda haftalik keshbek, bepul stavkalar va slot turnirlari muntazam o’tkaziladi.

    Saytda mahalliy va xalqaro to’lov vositalari past limitlar bilan mavjud.

  3689. 888starz_ftPl

    888starz O’zbekistondagi o’yinchilar uchun kazino va sport tikishlarini bitta rasmiy resursda taqdim etadi.
    Keno, Poker, Bingo va Aviator kabi formatlar doimo foydalanuvchi ixtiyorida.
    888starz uz [url=https://freewriterai.com/888starz-depozit-bonuslaridan-foydalanish/]888starz uz[/url]
    Rasmiy saytda mashhur va o’ziga xos sport turlarining keng ro’yxati mavjud.
    Depozit paytida 888UZ777 promokodidan foydalanish eng katta bonusni ta’minlaydi.
    Ro’yxatdan o’tish jarayoni tez va minimal ma’lumot talab qiladi.

  3690. Vivod iz zapoya na domy_wwmi

    Доброго времени, земляки. Кошмар случился. Соседи уже стучат в стену. В диспансер везти — позор на район. Короче, спасла только эта бригада — срочный вывод из запоя с выездом. Врач поставил систему сразу. В общем, цены и телефон тут — вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-jfw.ru]вывод из запоя[/url] Каждый час ухудшает состояние. Вдруг это спасёт чью-то жизнь.

  3691. Vivod iz zapoya na domy_jrSr

    Доброго времени суток. Брат не выходит из штопора. Соседи уже начали стучать в стену. В государственную наркологию — страшно и стыдно. Короче, выручила эта служба — срочный вывод из запоя с выездом. Через пару часов человек пришёл в себя. В общем, жмите, чтобы сохранить — вывод из запоя санкт петербург [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru[/url] Звоните прямо сейчас. Это может спасти чью-то жизнь.

  3692. Vivod iz zapoya na domy_xhPr

    Салют, Питер. Мой знакомый уже шестой день в запое. Дети боятся заходить в квартиру. Скорая не считается с алкоголиками. Короче, реально крутые специалисты — недорогой вывод из запоя в Санкт-Петербурге. Сняли острую интоксикацию. В общем, жмите, чтобы сохранить — вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-mnq.ru]вывод из запоя[/url] Не ждите, пока станет хуже. Вдруг это спасёт чью-то семью.

  3693. DonnyLOM

    Honest reaction is that I want to send this to a friend who would benefit from it, and a look at focusenablesvelocity added more material I will pass along too, the impulse to share is the strongest signal I have for content quality and this site is generating that impulse cleanly across multiple posts.

  3694. Vivod iz zapoya na domy_niSi

    Привет из Екатеринбурга. Случился ад. Жена плачет. Платная наркология — как счёт за квартиру. Короче, единственные кто приехал без предоплаты — недорогой вывод из запоя в Екатеринбурге. Прибыли через полчаса. В общем, жмите, чтобы не потерять — наркология вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru]https://vyvod-iz-zapoya-na-domu-ekaterinburg-dyz.ru[/url] Звоните прямо сейчас. Киньте ссылку нуждающимся.

  3695. Alexbug

    Liked how the writer used real examples instead of theoretical ones to make the points stick, and a stop at emynox added even more concrete examples, this is the kind of practical approach that respects readers who actually want to apply what they learn rather than just nodding along passively without doing anything useful.

  3696. HunterKaf

    Beyond the immediate post itself the editorial sensibility behind the site is what struck me, and a stop at soberviola continued displaying that sensibility, content that reveals editorial choices through accumulated reading is content with structural quality and this site has clearly developed an underlying approach worth identifying through multiple sessions of reading.

  3698. Vivod iz zapoya na domy_shsr

    Питер, привет. Брат не выходит из штопора. Соседи уже стучат в стену. Скорая не приедет на такой вызов. Короче, реально профессиональные врачи — вывод из запоя цены доступные. Приехали через 35 минут. В общем, контакты и цены тут — вывода из запоя 24 [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru[/url] Звоните прямо сейчас. Вдруг это спасёт чью-то жизнь.

  3699. Vivod iz zapoya na domy_fyMt

    Здорова, Питер. Отец не выходит из штопора. Мать плачет целыми днями. В бесплатный диспансер — стыд на всю жизнь. Короче, единственные, кто приехал без лишних вопросов — выведение из запоя на дому анонимно. Врач поставил систему сразу. В общем, не потеряйте — вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-xyt.ru]вывод из запоя[/url] Не тяните время. Киньте ссылку нуждающимся.

  3704. Vivod iz zapoya na domy_ytSr

    Здорова, народ. Случилась беда. Соседи уже начали стучать в стену. Платная клиника просит бешеные деньги. Короче, единственные, кто быстро приехал — вывод из запоя на дому круглосуточно. Сняли острую интоксикацию. В общем, вся инфа и контакты по ссылке — помощь вывода запоя нарколог 24 [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru[/url] Не ждите чуда. Киньте ссылку тем, кто в беде.

  3705. Vivod iz zapoya na domy_ovPr

    Салют, Питер. Брат снова ушёл в пьянку. Мать в депрессии. В государственный диспансер — табу. В итоге, единственные, кто быстро приехал и помог — капельница на дому от запоя. Врач сразу поставил капельницу. В общем, жмите, чтобы сохранить — вывод из запоя в спб [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-mnq.ru]вывод из запоя в спб[/url] Промедление убивает. Вдруг это спасёт чью-то семью.

  3706. Vivod iz zapoya na domy_xrmi

    Доброго времени, земляки. Брат снова ушёл в завязку. Мать на грани нервного срыва. Скорая не реагирует на такие вызовы. Короче, реально крутые врачи попались — вывод из запоя на дому круглосуточно. Сняли острую интоксикацию. В общем, жмите, чтобы сохранить — вывод из запоя недорого [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-jfw.ru]вывод из запоя недорого[/url] Каждый час ухудшает состояние. Вдруг это спасёт чью-то жизнь.

  3707. Vivod iz zapoya na domy_zvKn

    Здорова, народ. Брат не выходит из штопора. Соседи уже начали коситься. Скорая только забирает за 100 км. Короче, выручила эта служба — вывод из запоя цены фиксированные. Прибыли через 40 минут. В общем, вся инфа и контакты по ссылке — вывод из запоя клиника [url=https://vyvod-iz-zapoya-na-domu-nizhnij-novgorod-pwj.ru]вывод из запоя клиника[/url] Звоните прямо сейчас. Вдруг это спасёт чью-то жизнь.

  3709. Jerrycob

    Picked this site to mention to a colleague who would benefit, and a look at eshcap added more material I will pass along, recommending sites to colleagues is a higher bar than recommending to friends because the professional context demands more careful curation and this site cleared the professional bar without me having to think.

  3710. Vivod iz zapoya na domy_vjsr

    Питер, привет. Близкий человек снова сорвался. Мать плачет. Скорая не приедет на такой вызов. Короче, реально профессиональные врачи — вывод из запоя на дому срочно. Приехали через 35 минут. В общем, не потеряйте — вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru]вывод из запоя[/url] Каждый час ухудшает состояние. Перешлите тем, кто рядом с бедой.

  3711. SergioChits

    Now feeling the quiet pleasure of finding writing that takes itself seriously without being self serious, and a stop at progresswithoutdistraction extended that subtle pleasure, the gap between earnest and pretentious is fine and this site has clearly chosen to land on the earnest side without slipping over into pretentious which is impressive.

  3712. KareemAddem

    Now wishing I had found this site sooner, and a look at sergevermin extended that mild regret, the calculation of how many years of good content I missed by not finding the right sources earlier is one I try not to make too often but it does come up sometimes when I find sites this good.

  3714. Vivod iz zapoya v stacionare_cgPl

    Здорова, народ. Мой брат уже неделю в запое. Домашние условия не помогают. Скорая не решает проблему глобально. Короче, спасло только это — вывод из запоя стационарно под контролем врачей. Положили в палату на три дня. В общем, вся инфа по ссылке — запой стационар [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-knd.ru]https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-knd.ru[/url] Звоните прямо сейчас. Перешлите тем, кто в отчаянии.

  3719. Vivod iz zapoya na domy_weMt

    Доброго дня, земляки. Близкий человек снова сорвался в пьянку. Мать плачет целыми днями. Скорая не считается с запоями. Короче, реально крутые врачи — круглосуточный вывод из запоя с выездом. Прибыли через 40 минут. В общем, все контакты по ссылке — вывести из запоя цена [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-xyt.ru]вывести из запоя цена[/url] Звоните прямо сейчас. Киньте ссылку нуждающимся.

  3720. Vivod iz zapoya na domy_lgPr

    Всем привет с Невы. Отец не выходит из штопора. Дети боятся заходить в квартиру. Платная клиника — грабёж. Короче, выручила эта служба — недорогой вывод из запоя в Санкт-Петербурге. Врач сразу поставил капельницу. В общем, вся информация по ссылке — вывод из запоя нарколог24 [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-mnq.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-mnq.ru[/url] Не ждите, пока станет хуже. Вдруг это спасёт чью-то семью.

  3721. Vivod iz zapoya na domy_vkSr

    Всем привет из Питера. Мой отец уже четвёртые сутки в запое. Дети боятся заходить в комнату. Скорая не приедет на такой вызов. Короче, реально профессиональные врачи — срочный вывод из запоя с выездом. Сняли острую интоксикацию. В общем, не потеряйте — выведение из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru[/url] Не ждите чуда. Киньте ссылку тем, кто в беде.

  3722. Vivod iz zapoya na domy_ksmi

    Приветствую народ. Отец не выходит из штопора. Родственники не знают, как помочь. Платная клиника — бешеные счета. Короче, спасла только эта бригада — недорогой вывод из запоя в Питере. Приехали за 30 минут. В общем, не потеряйте — выведение из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-jfw.ru]выведение из запоя на дому[/url] Каждый час ухудшает состояние. Вдруг это спасёт чью-то жизнь.

  3723. Samsonfueta

    Now noticing the post fit a particular gap in my reading without my having articulated the gap before, and a look at acornharborcommercegallery extended that gap filling effect, content that meets needs I had not consciously formulated is content with reader insight and this site has clearly developed that anticipatory editorial sense across many pieces.

  3724. Vivod iz zapoya na domy_uhsr

    Доброго дня, земляки. Мой отец уже третьи сутки в запое. Родственники не знают, за что хвататься. Платная клиника — деньги выкачивают. Короче, реально профессиональные врачи — капельница от запоя на дому. Через пару часов человек пришёл в себя. В общем, контакты и цены тут — вывод из запоя с выездом на дом [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru[/url] Звоните прямо сейчас. Перешлите тем, кто рядом с бедой.

  3725. Gregorybum

    Approaching this site through a casual link click and being surprised by what I found, and a look at eshpyx extended the surprise, the rare experience of stumbling into excellent independent content rather than predictable mediocrity is one of the actual remaining pleasures of casual web browsing and this site provided it cleanly.

  3726. FloydDials

    Came here from a search and stayed for the side links because they were that interesting, and a stop at uptonvelour took me even further into the site, the kind of organic exploration that good content invites is something most sites kill through aggressive interlinking and pushy navigation choices rather than relying on quality.

  3727. AndyNup

    A piece that ended with a clean landing rather than fading out, and a look at growthneedsmomentum maintained the same crisp conclusions, endings that resolve rather than dissolve are a sign of careful structural thinking and this site has clearly invested in how its pieces conclude rather than letting them simply run out of energy.

  3728. Vivod iz zapoya na domy_bwSr

    Приветствую земляков. Брат не выходит из штопора. Дети боятся заходить в комнату. В государственную наркологию — страшно и стыдно. Короче, единственные, кто быстро приехал — выведение из запоя на дому с капельницей. Через пару часов человек пришёл в себя. В общем, цены и телефон тут — вывод из запоя на дому спб [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru[/url] Звоните прямо сейчас. Это может спасти чью-то жизнь.

  3729. Vivod iz zapoya na domy_qrPr

    Салют, Питер. Мой знакомый уже шестой день в запое. Дети боятся заходить в квартиру. В государственный диспансер — табу. В итоге, реально крутые специалисты — недорогой вывод из запоя в Санкт-Петербурге. Через пару часов человек задышал ровно. В общем, не потеряйте контакт — вывод из запоя цены [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-mnq.ru]вывод из запоя цены[/url] Не ждите, пока станет хуже. Перешлите тем, кто рядом с бедой.

  3730. Vivod iz zapoya na domy_jemi

    Доброго времени, земляки. Брат снова ушёл в завязку. Дети боятся оставаться с отцом. Скорая не реагирует на такие вызовы. Короче, реально крутые врачи попались — капельница от запоя на дому. Приехали за 30 минут. В общем, не потеряйте — помощь вывода запоя нарколог 24 [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-jfw.ru]помощь вывода запоя нарколог 24[/url] Каждый час ухудшает состояние. Перешлите тем, кто рядом с бедой.

  3731. Vivod iz zapoya na domy_pasr

    Доброго дня, земляки. Мой отец уже третьи сутки в запое. Мать плачет. В наркологию тащить — страшно. Короче, единственные, кто быстро приехал — недорогой вывод из запоя в Санкт-Петербурге. Через пару часов человек пришёл в себя. В общем, контакты и цены тут — вывод из запоя спб [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru[/url] Звоните прямо сейчас. Вдруг это спасёт чью-то жизнь.

  3732. Vivod iz zapoya v stacionare_cpPl

    Всем привет. Ситуация критическая. Нужно серьёзное наблюдение специалистов. Платные клиники — дорого и непонятно. Короче, действительно эффективный метод — вывод из запоя в стационаре круглосуточно. Врачи наблюдали 24/7. В общем, не потеряйте контакты — прокапаться в стационаре [url=https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-knd.ru]https://vyvod-iz-zapoya-v-staczionare-nizhnij-novgorod-knd.ru[/url] Звоните прямо сейчас. Это может спасти чью-то семью.

  3733. Vivod iz zapoya na domy_snMt

    Приветствую народ. Кошмар полный. Мать плачет целыми днями. Скорая не считается с запоями. Итог, единственные, кто приехал без лишних вопросов — вывод из запоя на дому срочно. К утру человек пришёл в сознание. В общем, все контакты по ссылке — круглосуточный вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-xyt.ru]круглосуточный вывод из запоя[/url] Промедление может стоить здоровья. Вдруг это спасёт чью-то жизнь.

  3734. Vivod iz zapoya na domy_oaSa

    Всем привет из Питера. Брат снова ушёл в завязку. Дети боятся оставаться с отцом. Скорая не считается с запойными. Короче, реально профессиональные врачи — круглосуточный вывод из запоя с выездом. Врач поставил систему. В общем, вся информация по ссылке — вывод из запоя на дому [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-hnd.ru]вывод из запоя на дому[/url] Не ждите. Вдруг это спасёт чью-то жизнь.

  3735. Vivod iz zapoya na domy_fska

    Привет, народ. Мой брат уже неделю в запое. Дети ходят как в воду опущенные. Скорая не приезжает на такие вызовы. Итог, реально крутые специалисты — недорогой вывод из запоя в Санкт-Петербурге. Сняли интоксикацию. В общем, вся инфа по ссылке — вывод из запоя с выездом на дом [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-rpl.ru]вывод из запоя с выездом на дом[/url] Не тяните. Вдруг это спасёт чью-то семью.

  3736. Rileyslofe

    Liked the natural conversational tone throughout, never stiff and never overly casual either, and a stop at exabuff kept that comfortable middle ground going, finding a tone that respects the reader without becoming distant or overly familiar is harder than it sounds and this site nails that balance consistently across many different pieces.

  3737. Colbychuts

    Found the use of subheadings really helpful for scanning back through the post later, and a stop at tomatotiara kept that reader friendly approach going, navigation is something many blog writers ignore but small structural choices make a noticeable difference for someone returning to find a specific point again days or weeks later.

  3738. Narkologicheskaya pomosh_csMl

    Привет из Нижнего. Брат уже пятые сутки не просыхает. Дети напуганы до смерти. В диспансер тащить — позор на район. В общем, единственные, кто быстро отреагировал — частная наркологическая помощь анонимно. Врач осмотрел и поставил капельницу. В общем, жмите, чтобы сохранить — наркологическая клиника цены на услуги [url=https://narkologicheskaya-pomoshh-nizhnij-novgorod-fql.ru]https://narkologicheskaya-pomoshh-nizhnij-novgorod-fql.ru[/url] Не медлите. Отправьте тем, кто рядом с бедой.

  3741. OctavioVag

    Skipped the related products section because there was none, and a stop at alpinecovemerchantgallery also lacked any aggressive monetisation, content that is not constantly trying to convert me into a customer or subscriber is content that has confidence in its own value and that confidence shows up as a different reading experience.

  3742. Vivod iz zapoya na domy_ucPr

    Всем привет с Невы. Жесть полная. Дети боятся заходить в квартиру. В государственный диспансер — табу. Короче, выручила эта служба — вывод из запоя на дому круглосуточно. Сняли острую интоксикацию. В общем, жмите, чтобы сохранить — круглосуточный вывод из запоя [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-mnq.ru]круглосуточный вывод из запоя[/url] Звоните прямо сейчас. Вдруг это спасёт чью-то семью.

  3743. Vivod iz zapoya na domy_gzSr

    Доброго времени суток. Мой отец уже четвёртые сутки в запое. Соседи уже начали стучать в стену. Скорая не приедет на такой вызов. Короче, реально профессиональные врачи — выведение из запоя на дому с капельницей. Врач сразу поставил систему. В общем, вся инфа и контакты по ссылке — врач капельница алкоголь на дом [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru[/url] Каждый час ухудшает состояние. Киньте ссылку тем, кто в беде.

  3744. Vivod iz zapoya na domy_xysr

    Питер, привет. Брат не выходит из штопора. Соседи уже стучат в стену. Скорая не приедет на такой вызов. Короче, единственные, кто быстро приехал — вывод из запоя цены доступные. Сняли абстинентный синдром. В общем, жмите, чтобы сохранить — капельница от алкоголя на дому спб [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru[/url] Звоните прямо сейчас. Перешлите тем, кто рядом с бедой.

  3745. Vivod iz zapoya na domy_ggmi

    Здорово, Питер. Кошмар случился. Мать на грани нервного срыва. Платная клиника — бешеные счета. Короче, спасла только эта бригада — капельница от запоя на дому. Сняли острую интоксикацию. В общем, не потеряйте — вывод из алкогольного запоя нарколог 24 [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-jfw.ru]вывод из алкогольного запоя нарколог 24[/url] Не ждите чуда. Перешлите тем, кто рядом с бедой.

  3746. Vivod iz zapoya na domy_sgSa

    Салют, земляки. Беда случилась. Дети боятся оставаться с отцом. Скорая не считается с запойными. Короче, реально профессиональные врачи — круглосуточный вывод из запоя с выездом. Приехали через 40 минут. В общем, вся информация по ссылке — вывод из запоя нарколог 24 [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-hnd.ru]вывод из запоя нарколог 24[/url] Звоните прямо сейчас. Вдруг это спасёт чью-то жизнь.

  3747. Nevillezed

    Started a draft response in my head and ended without publishing it because the post said it well enough, and a look at forwardtractioncreated produced the same effect, content that satisfies my urge to add to it by being complete enough on its own is rare and represents a particular kind of editorial completeness here.

  3748. ElijahWhace

    Will be sharing this with a couple of people who care about the topic, and a stop at ezabond added more material worth passing along, the kind of site that is generous with quality content and does not make you jump through hoops to access it which is appreciated more than the team probably realises.

  3749. Vivod iz zapoya na domy_uzMt

    Приветствую народ. Кошмар полный. Мать плачет целыми днями. Скорая не считается с запоями. Короче, единственные, кто приехал без лишних вопросов — недорогой вывод из запоя в Санкт-Петербурге. Сняли абстинентный синдром. В общем, жмите, чтобы сохранить — вывод из запоя в домашних условиях нарколог 24 [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-xyt.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-xyt.ru[/url] Не тяните время. Киньте ссылку нуждающимся.

  3750. Vivod iz zapoya na domy_vnka

    Доброго времени суток. Ужас случился. Соседи уже начали звонить в полицию. Скорая не приезжает на такие вызовы. Итог, единственные, кто приехал без лишних вопросов — срочный вывод из запоя с капельницей. К утру человек пришёл в норму. В общем, вся инфа по ссылке — вывод из запоя недорого [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-rpl.ru]вывод из запоя недорого[/url] Не тяните. Перешлите тем, кто в беде.

  3751. BillySnola

    При алкогольной интоксикации важно учитывать общее состояние здоровья, поэтому самостоятельные решения могут быть небезопасны. Медицинский осмотр помогает определить необходимый объем помощи https://spravochnik-anatomia.ru/kapelniczy-na-dom-ot-zapoya-kogda-eto-umestno-chto-v-sostave-i-kak-ne-navredit/

  3752. Vivod iz zapoya na domy_xvSa

    Всем привет из Питера. Брат снова ушёл в завязку. Дети боятся оставаться с отцом. Скорая не считается с запойными. Короче, единственные, кто быстро приехал — вывод из запоя на дому срочно. Через пару часов человек пришёл в себя. В общем, вся информация по ссылке — вывод из запоя цена [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-hnd.ru]вывод из запоя цена[/url] Каждый час ухудшает состояние. Вдруг это спасёт чью-то жизнь.

  3753. Ryderted

    Bookmark earned and the bookmark feels like a permanent addition rather than a maybe, and a look at vaporsalt confirmed that permanent status, the difference between durable bookmarks and ephemeral ones is something I have learned to feel quickly and this site triggered the durable feeling almost immediately during my first read here.

  3755. Vivod iz zapoya na domy_vaSr

    Здорова, народ. Случилась беда. Мать на грани истерики. В государственную наркологию — страшно и стыдно. Короче, единственные, кто быстро приехал — помощь на дому без учёта. Сняли острую интоксикацию. В общем, жмите, чтобы сохранить — врач капельница алкоголь на дом [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-abc.ru[/url] Каждый час ухудшает состояние. Киньте ссылку тем, кто в беде.

  3756. Vivod iz zapoya na domy_lrPr

    Всем привет с Невы. Отец не выходит из штопора. Родные просто в отчаянии. Скорая не считается с алкоголиками. В итоге, реально крутые специалисты — вывод из запоя цены фиксированные. Врач сразу поставил капельницу. В общем, цены и телефон тут — вывести из запоя цена [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-mnq.ru]вывести из запоя цена[/url] Не ждите, пока станет хуже. Перешлите тем, кто рядом с бедой.

  3757. Vivod iz zapoya na domy_usmi

    Доброго времени, земляки. Близкий человек уже пятые сутки в запое. Соседи уже стучат в стену. Скорая не реагирует на такие вызовы. Короче, единственные, кто приехал быстро — вывод из запоя на дому круглосуточно. Врач поставил систему сразу. В общем, цены и телефон тут — вывод из запоя на дому спб цены [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-jfw.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-jfw.ru[/url] Не ждите чуда. Перешлите тем, кто рядом с бедой.

  3758. Vivod iz zapoya na domy_sxsr

    Питер, привет. Мой отец уже третьи сутки в запое. Мать плачет. В наркологию тащить — страшно. Короче, единственные, кто быстро приехал — выведение из запоя на дому анонимно. Сняли абстинентный синдром. В общем, контакты и цены тут — вывод из запоя нарколог 24 [url=https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru]https://vyvod-iz-zapoya-na-domu-sankt-peterburg-zqe.ru[/url] Не ждите. Вдруг это спасёт чью-то жизнь.

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio